ВычМат_Лекции_2013_1 / Лекции Матлаб, программы и задачи к ним / 6 лекция Матлаб (Продолжение численных методов) / 6 лекция Матлаб (Продолжение численных методов)
.docxМАТЛАБ. ПРОДОЛЖЕНИЕ ЧИСЛЕННЫХ МЕТОДОВ.
Нелинейные
уравнения и системы.
Численное решение уравнения f(x)=0
часто проводят в два этапа. На первом
этапе отделяют корни уравнения, то есть
определяют интервалы изоляции корня.
Например, график функции пересекает
ось Х и окрестности точки пересечения
(или нескольких таких точек) это и есть
интервалы изоляции корня. На втором
этапе проводят уточнение, то есть сужают
интервал изоляции корня до ширины,
равной заданной погрешности по Х.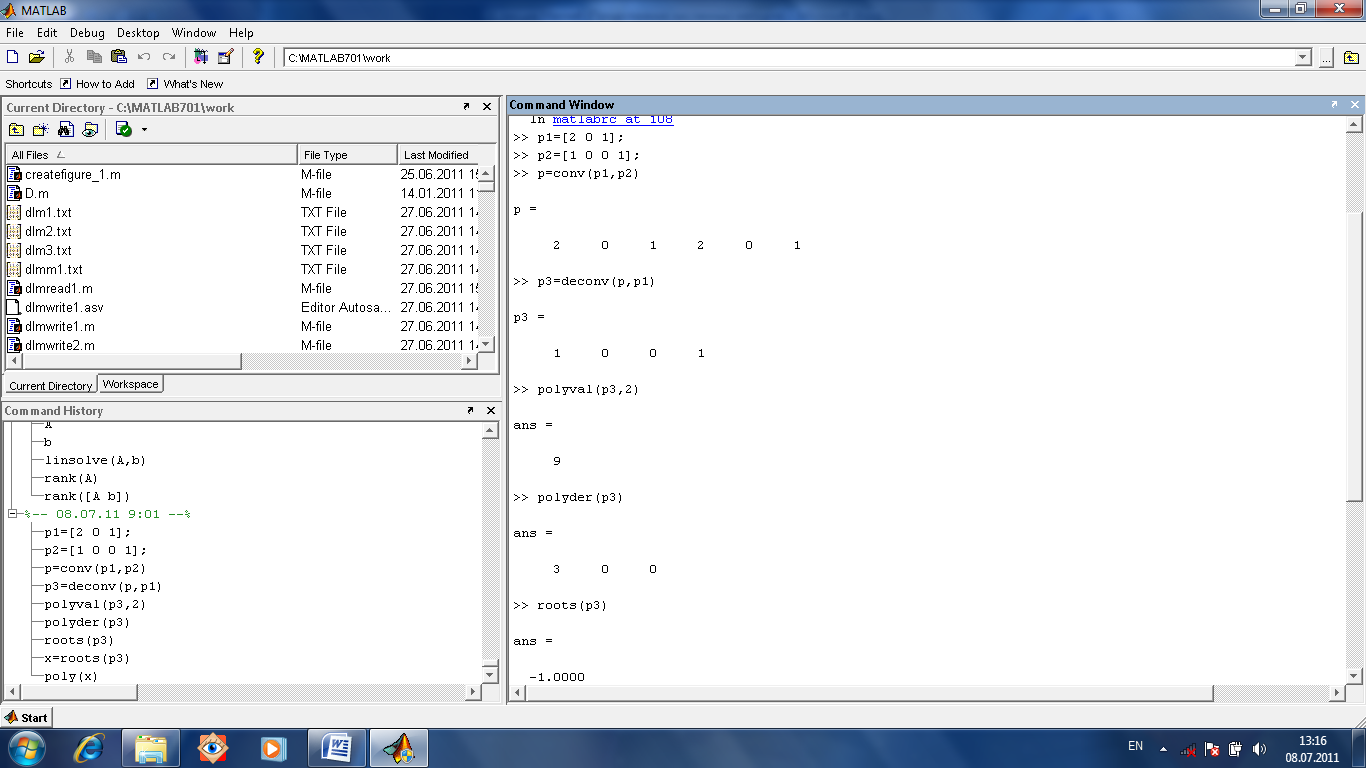
Алгебраическое уравнение, оно же полином, оно же многочлен a0xn+a1xn-1+a2xn-2+…+an-1x+an=0
Его вектор коэффициентов p=[a0 a1 a2…an-1 an]
Произведение двух полиномов вычисляет функция conv(p1,p2) которой передаются векторы коэффициентов обоих полиномов. Деление полиномов (первого на второй) осуществляет функция [q r]=deconv(p1,p2), которая возвращает ответ и остаток от деления.
Если
надо вычислить значение полинома при
определенном значении х, то для этого
используется функция polyval(p1,x).
Нахождение производной от полинома
осуществляется функцией polyder.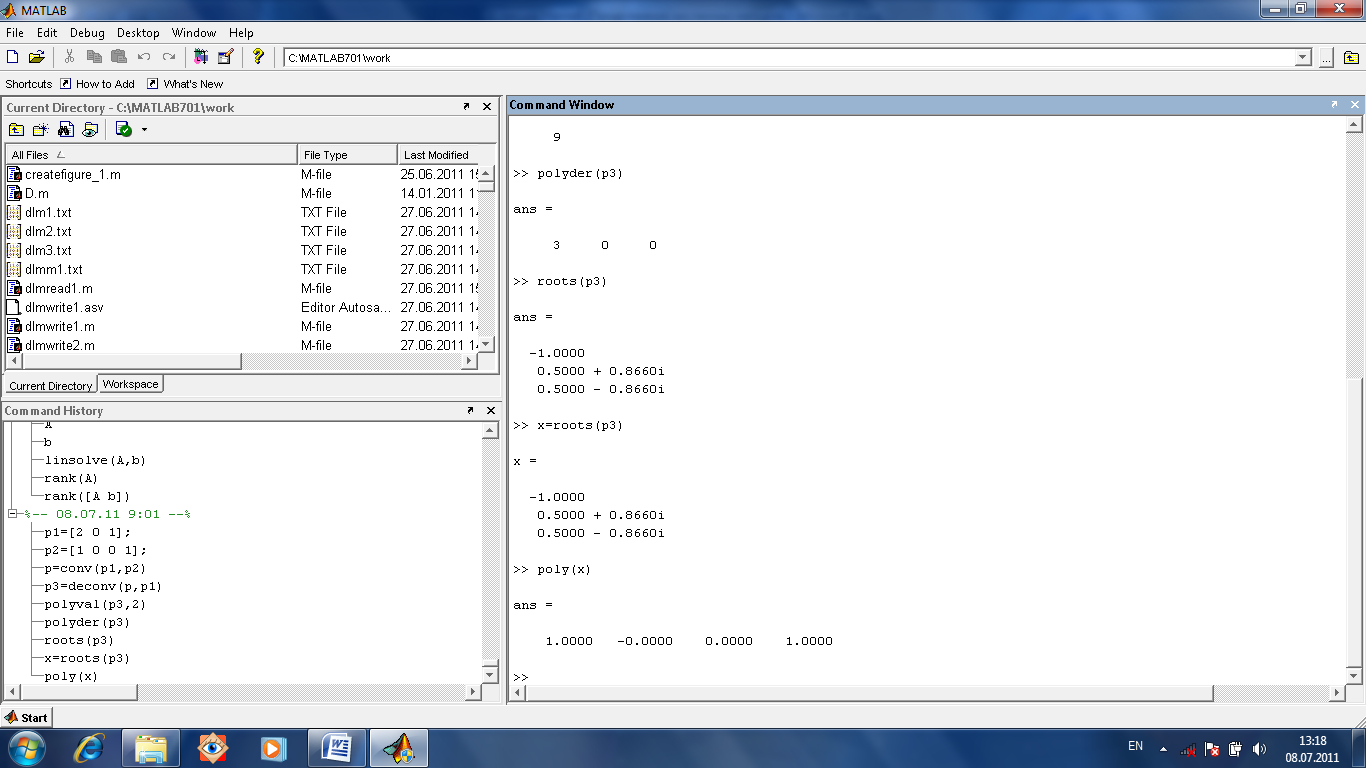
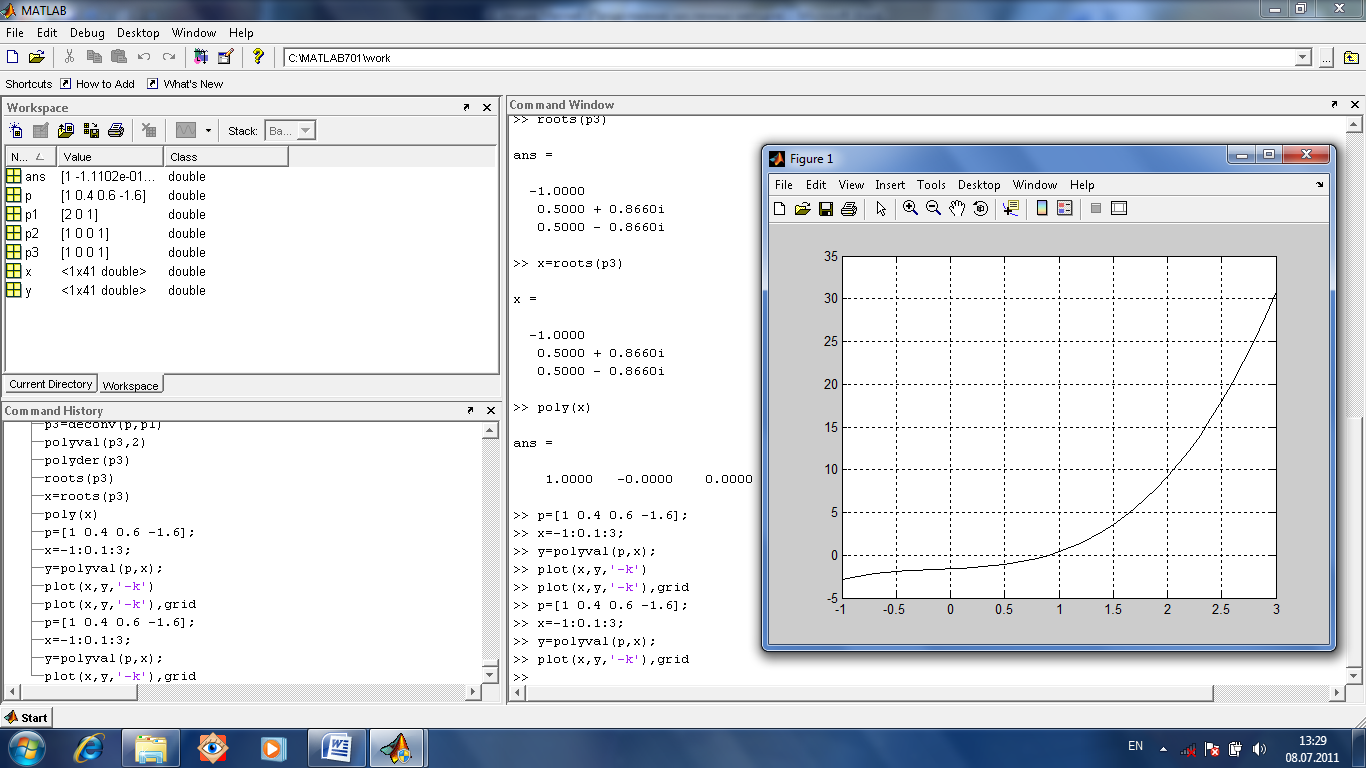
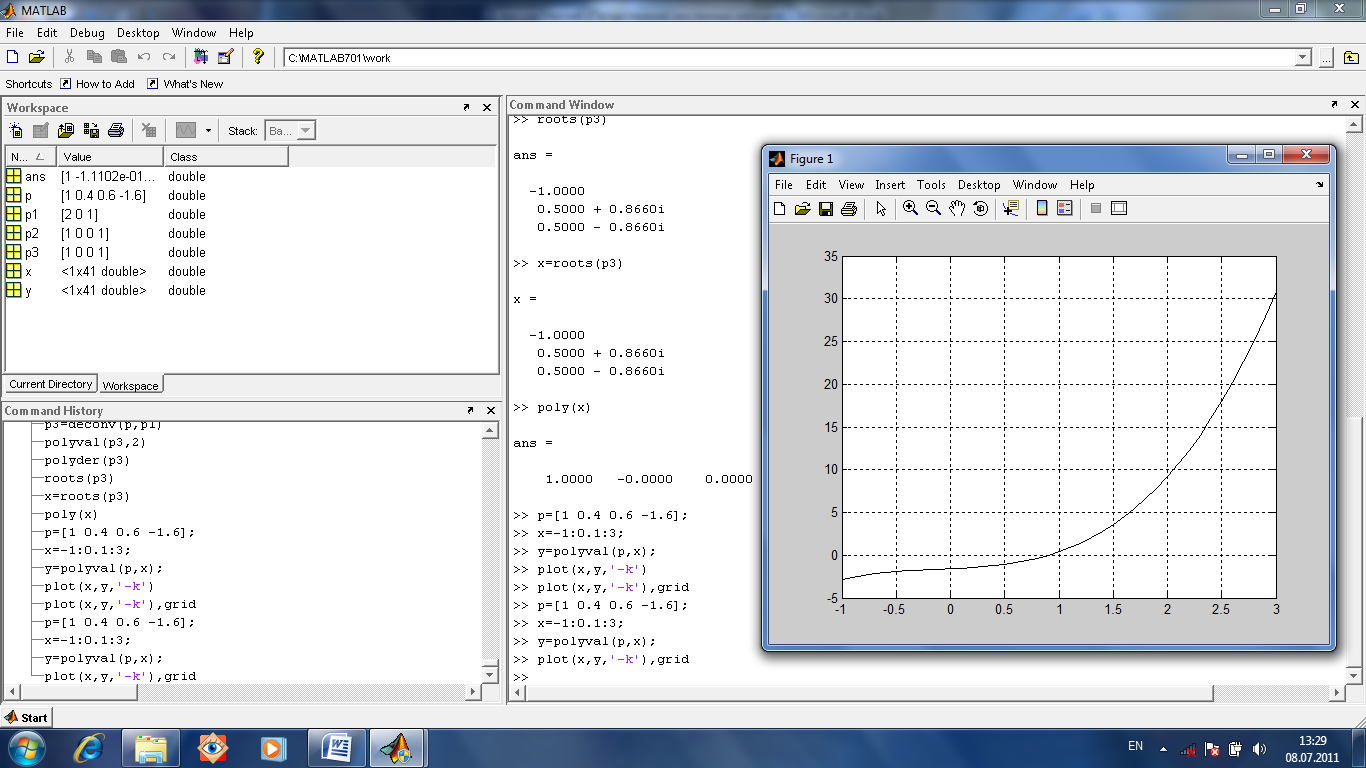
Для нахождения корней многочлена есть функция roots(p). Наоборот, построить полином по вектору его корней может функция poly(x).
С помощью функции polyval можно получить графическое решение уравнения.
Трансцендентные
уравнения.
К
ним относятся показательные,
логарифмические, тригонометрические.
Для их решения используется функция
fzero(‘name’,x)
где х начальное приближение к корню или
интервал его изоляции. Само трансцендентное
уравнение описано в М-файле.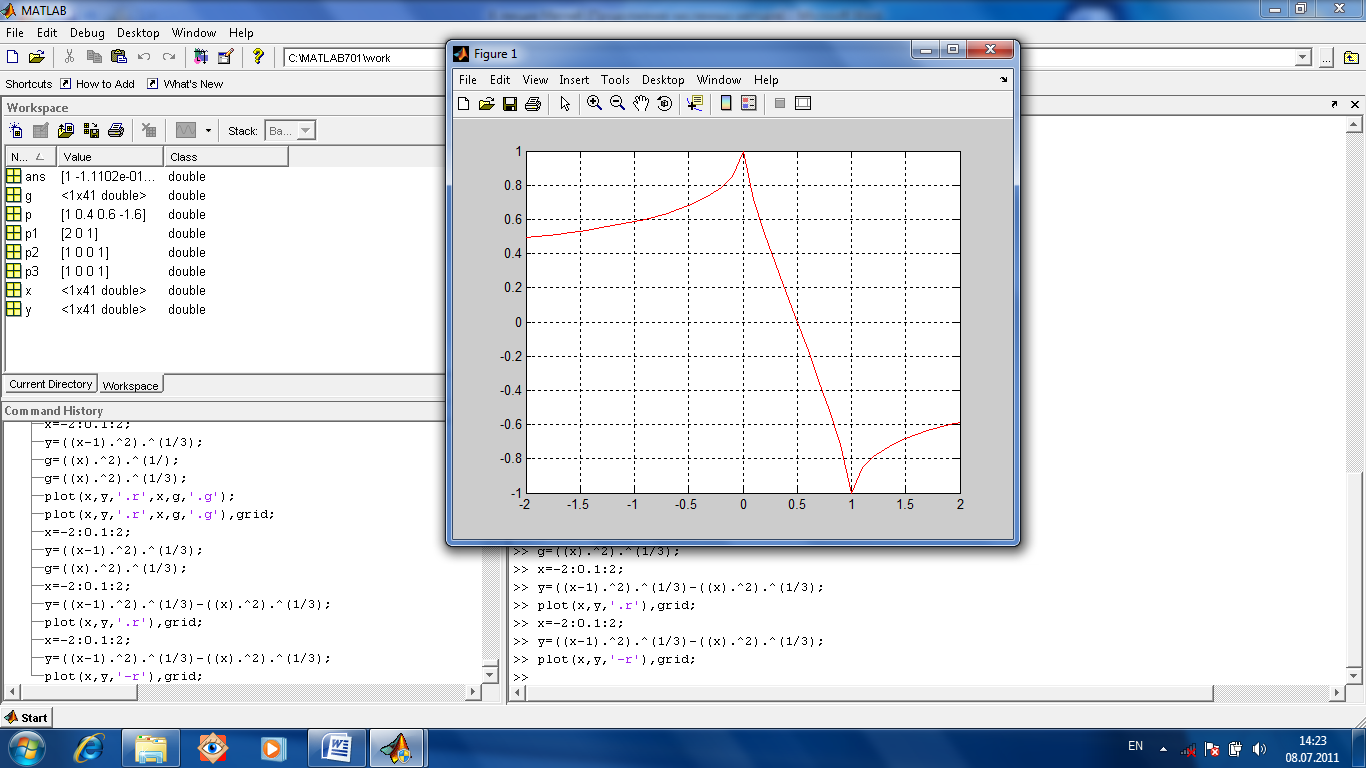
Рекомендуется по возможности построить график. Потом уже описать функцию в М-файле. Затем использовать функцию fzero для нахождения корня.
Если
график покажет, что уравнение имеет
несколько корней, то следует для каждого
из корней определить интервал изоляции
и использовать его в вызове функции
fzero
(для каждого из корней по отдельности),
то есть к функции придется обратиться
несколько раз.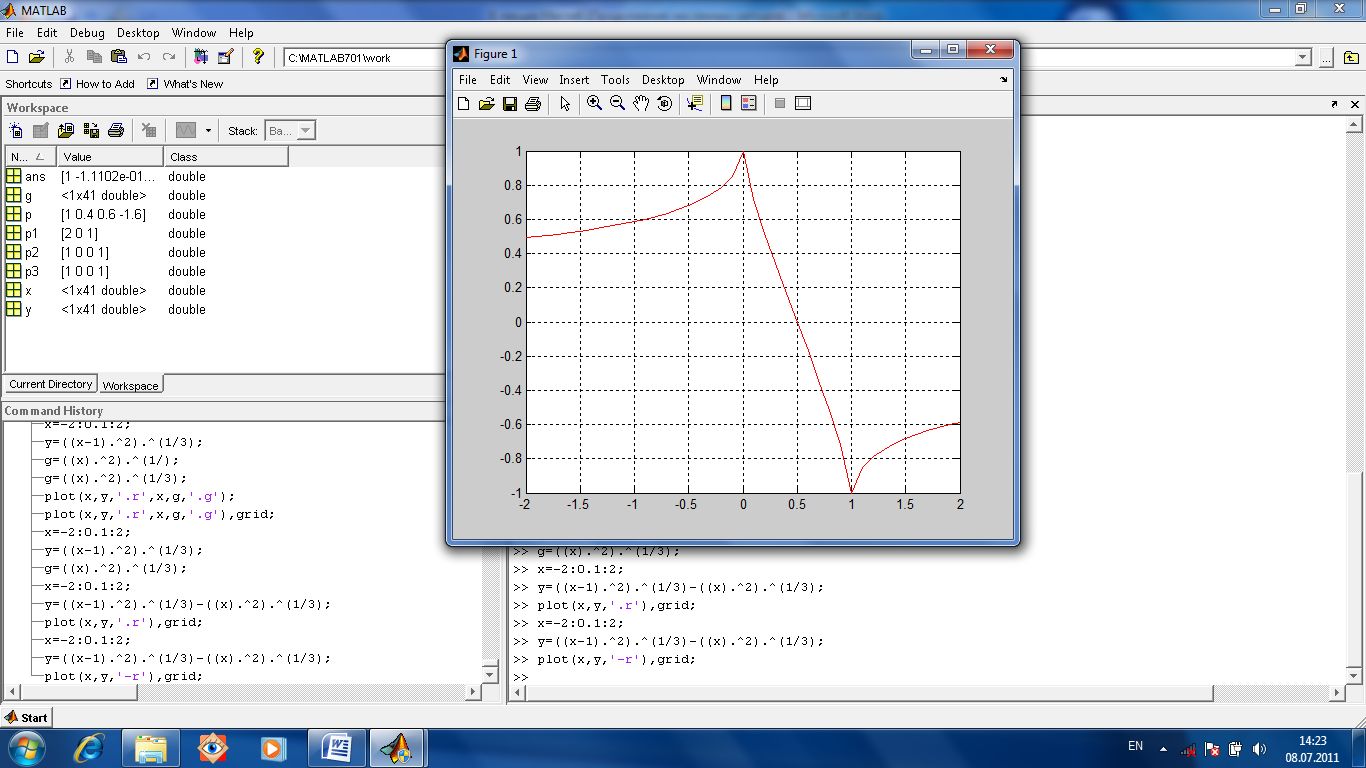
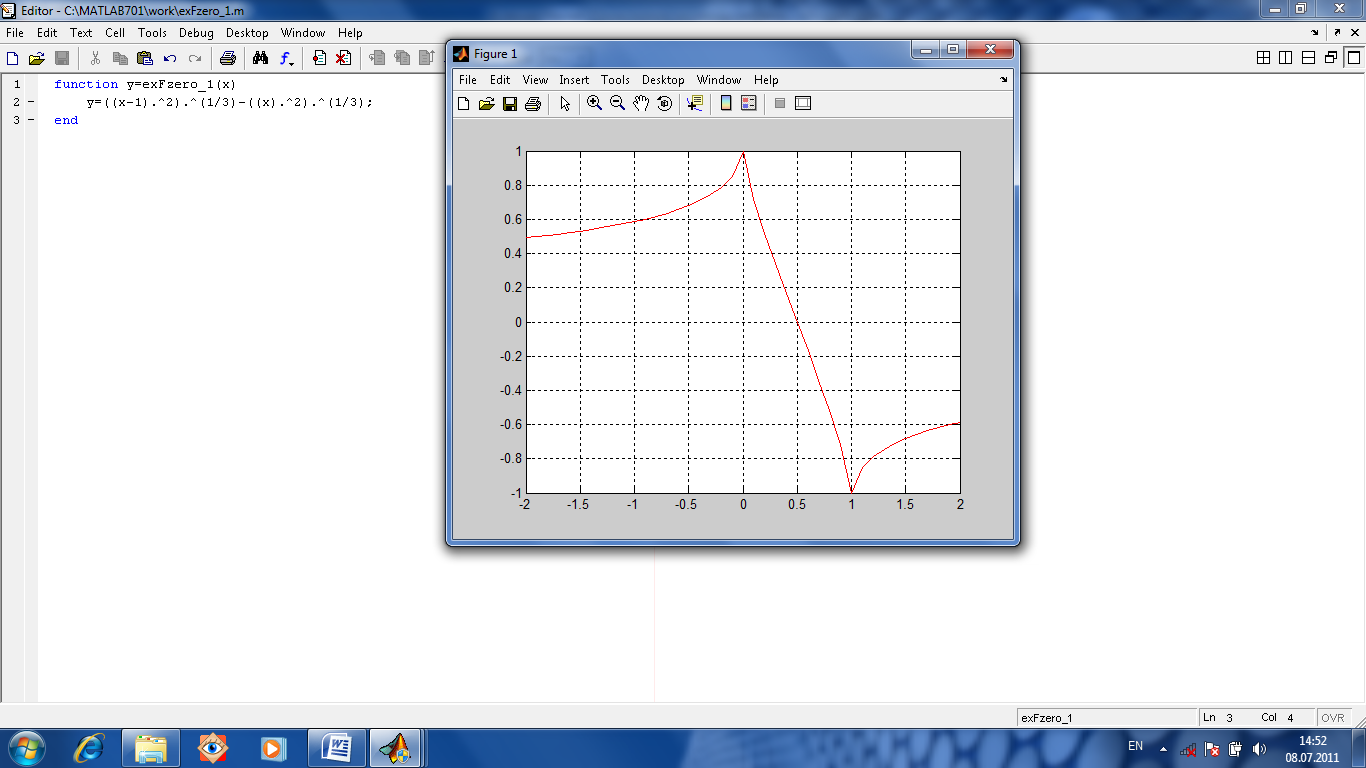
При
вызове функции fzero
возвращаются только вещественные числа.
Комплексные (мнимые) корни она не
вычисляет.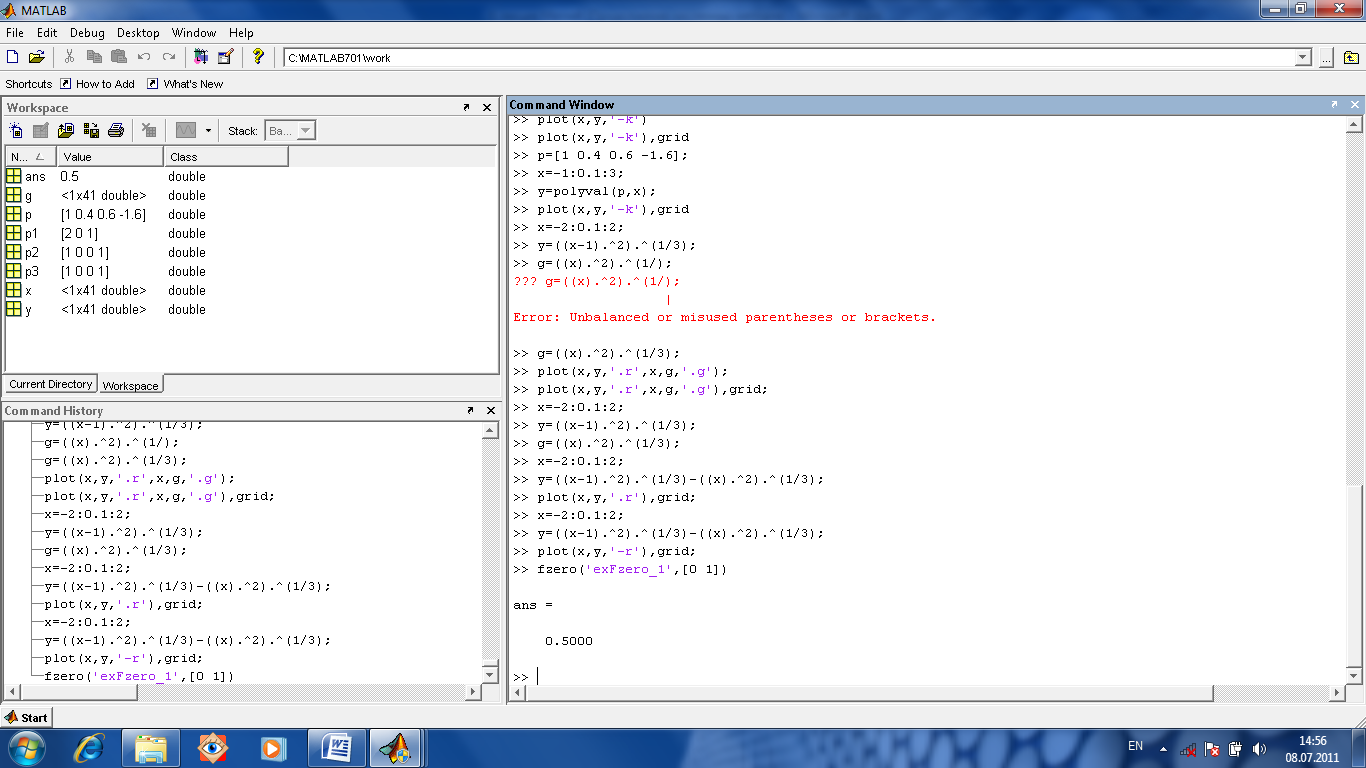
Численное интегрирование. Для интегрирования существует очень много алгоритмов в современной вычислительной математике. Будем рассматривать выборочно некоторые из них.
Интегрирование
методом трапеций означает, что
подинтегральная площадка разбивается
на трапециевидные подплощадки, границы
между трапециями это вертикальные
линии, проведенные через x1,
x2,
… , xn
равноотстоящие точки на оси Х, идущие
от начала до конца интервала интегрирования
[x1
xn].
Верхние границы трапеций это отрезки,
соединяющие точки f(x1),
f(x2),
… , f(xn).
Нижние границы трапеций ось Х. 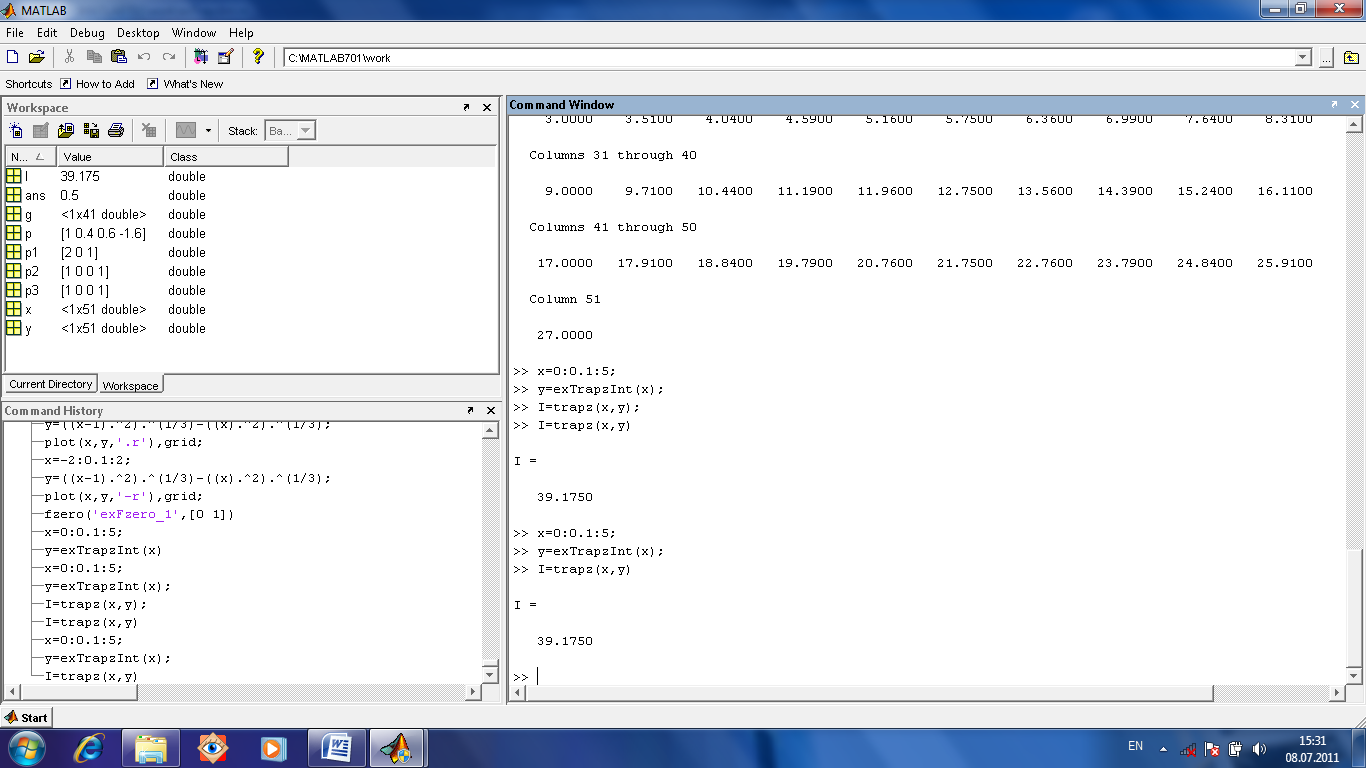
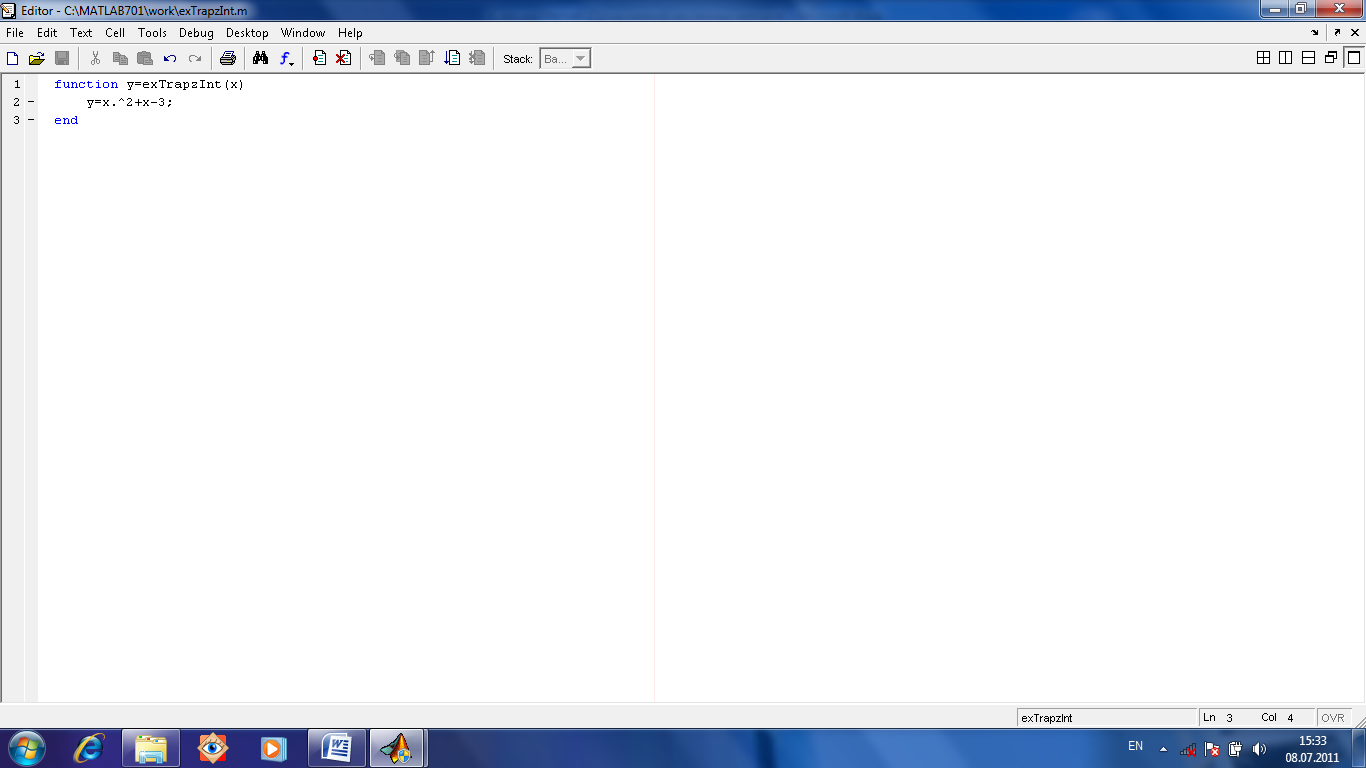
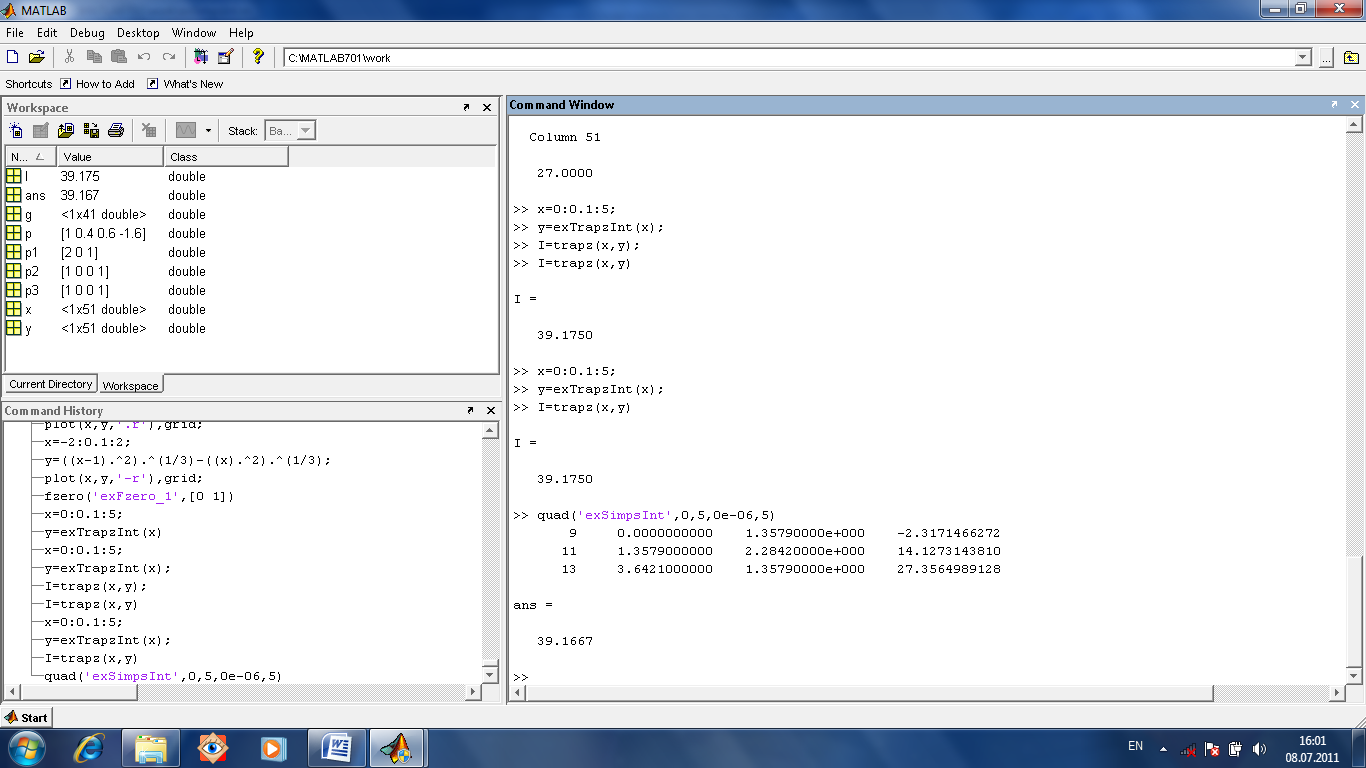
Для метода трапеций есть функция trapz(x,y).
При интегрировании методом Симпсона верхние границы подплощадок являются отрезками параболы. Для него есть функция quad(‘name’,a,b,tol,trace), где перечислены аргументы имя М-функции, левая и правая границы интегрирования, точность вычислений, а также параметр задающий таблицу с промежуточными точками результатами вычислений.
Есть также весьма точный алгоритм Ньютона-Котеса 8-го порядка. Он вызывается функцией quad8(‘name’,a,b,tol,trace).
Обыкновенные дифференциальные уравнения и системы.
Дифференциальным уравнением n-го порядка называется уравнение:
H(t, x, x’, x’’, … , x(n))=0
Решением дифференциального уравнения называется функция x(t), которая обращает уравнение в тождество.
Системой дифференциальных уравнений n-го порядка называется система вида:
x1’=f1(t,
x1,
x2,
x3,
… , xn)
x2’=f1(t, x1, x2, x3, … , xn)
…………………………..
xn’=f1(t, x1, x2, x3, … , xn)
Системой линейных дифференциальных уравнений называют систему вида:
x1’=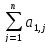 xj
+ b1
xj
+ b1
x2’=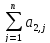 xj
+ b1
xj
+ b1
.…………………..
xn’=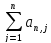 xj
+ b1
xj
+ b1
Решением системы является вектор x(t)=x1(t), x2(t), … ,xn(t), который обращает вышеприведенные системы уравнений в тождества.
Различают:
Задачу Коши, когда все дополнительные условия заданы в одной (чаще всего в начальной) точке интервала значений t.
Краевую задачу, когда дополнительные условия заданы на границах интервала значений t.
Есть много встроенных функций, обеспечивающих решение вышеуказанных задач.
Ниже описаны некоторые из них с примерами их использования.
Входными параметрами этих функций являются:
-
f вектор-функция для вычисления правой части уравнения вида x’=f(x,t), удовлетворяющей начальному условию x(t0)=x0 или системы дифференциальных уравнений, данных в матричном виде dx/dt=f(t,x) с начальным условием x(t0)=x0 данным в матричном виде.
-
interval массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы.
-
X0 вектор начальных условий системы дифференциальных уравнений.
-
options параметры управления ходом решения дифференциального уравнения или системы уравнений.
Все функции возвращают:
-
Массив Т содержащий координаты узлов сетки, в которых ищется решение.
-
Матрицу Х в которой i-й столбец является значением вектор-функции решения в узле Ti.
Решим
задачу Коши: dx/dt
+ x
=sin
xt
при x(0)=1.5.
Напишем М-функцию. Используем функцию
ode113,
которая реализует метод Адамса. В
качестве ее параметров используются:
@D
ссылка на М-функцию, [0 35] интервал
интегрирования уравнения, начальное
условие x(0)=1.5
указано в виде 1,5 на соответствующем
месте в списке параметров.
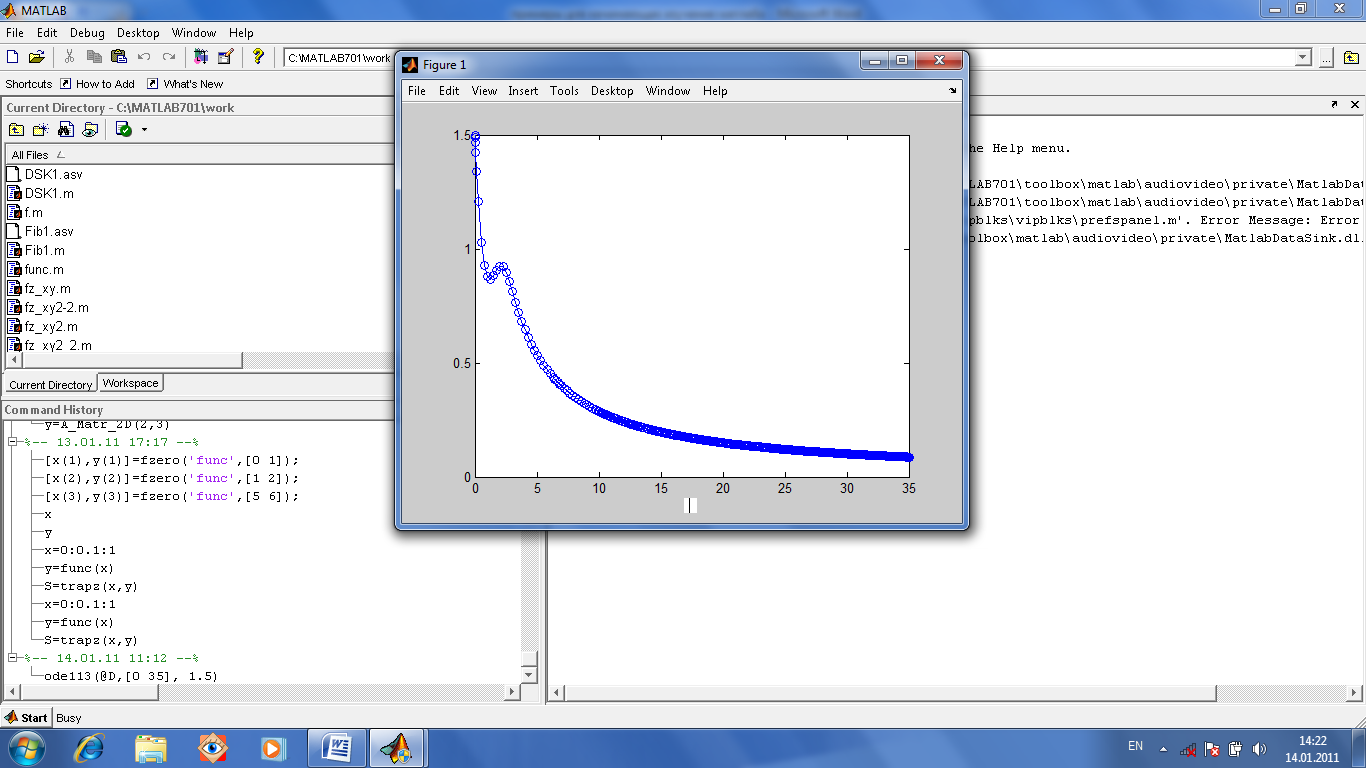
Обращение к функции:
ode113(@D,
[0 35], 1.5). Она строит график решения.
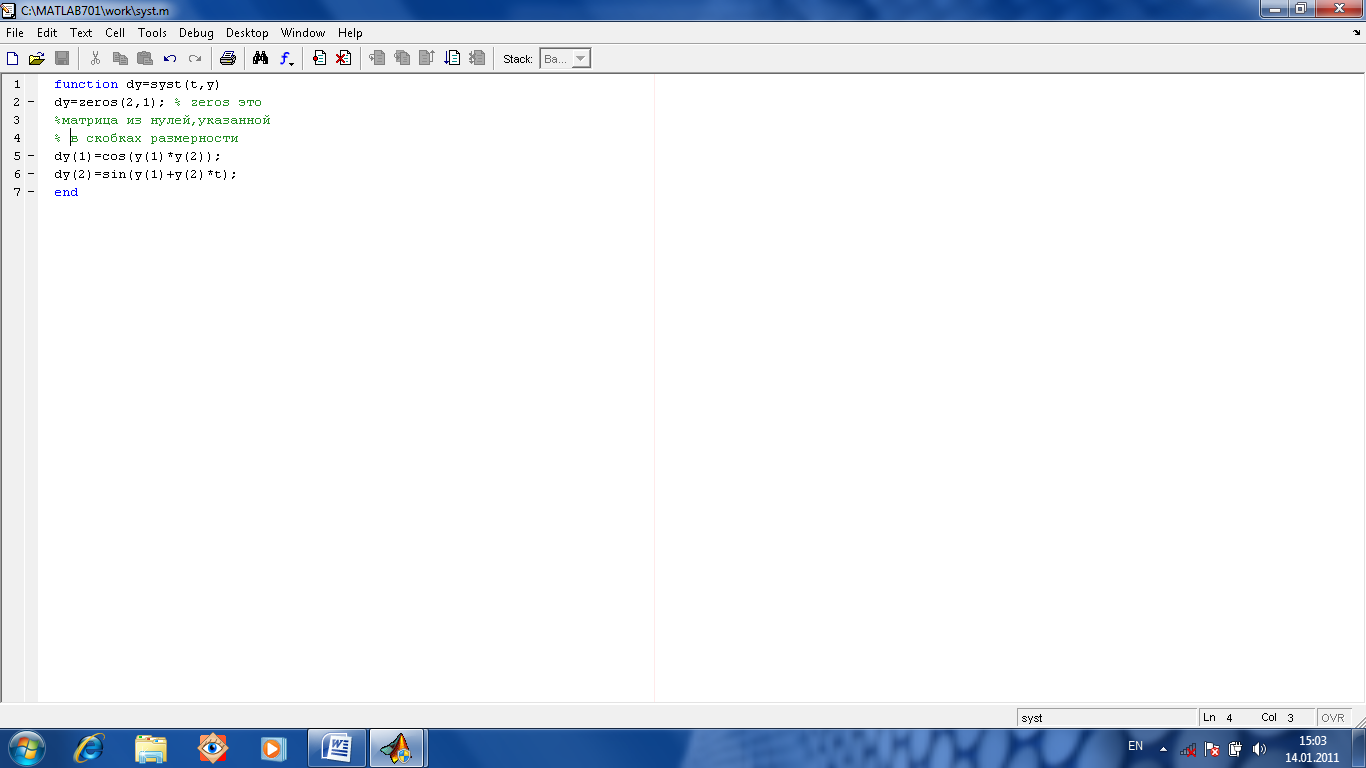
Решим систему на интервале [0 10] при y1(0)=0,
y1/=cos(y1y2)
y2(0)=0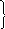
y2/=sin(y1+ty2)
Напишем М-функцию syst.
Используем функцию ode23
решающую методом Рунге-Кутта 2-3 порядка.
Ее вызов [T,
Y]=ode23(@syst,
[0 10], [0 0]); где явно указаны выходные
параметры вектор Т и матрица Y,
а также указаны интервал [0 10] и начальные
значения 
[0 0]. Затем формируем график решения plot(T,Y(:,1)’-r’,T,Y(:,2),’-k‘). Получаем график.
Решение жестких задач. Для решения жестких задач действуют в два этапа. Сначала убеждаются, что система жесткая (действительные части всех собственных чисел матрицы dx/dt=B отрицательны и величина s=max|Re(h)|/min|Re(h)|, называемая числом жесткости системы, велика). После этого решают систему с помощью соответствующих функций матпакета.
Найдем решение задачи Коши для следующей системы:
119.46
185.38 126.88 121.03
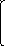
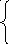
dX = -10.395 -10.136 -3.636 8.577 X
dt -53.302 -85.932 -63.182 54.211
-115.58 -181.75 -112.8 -199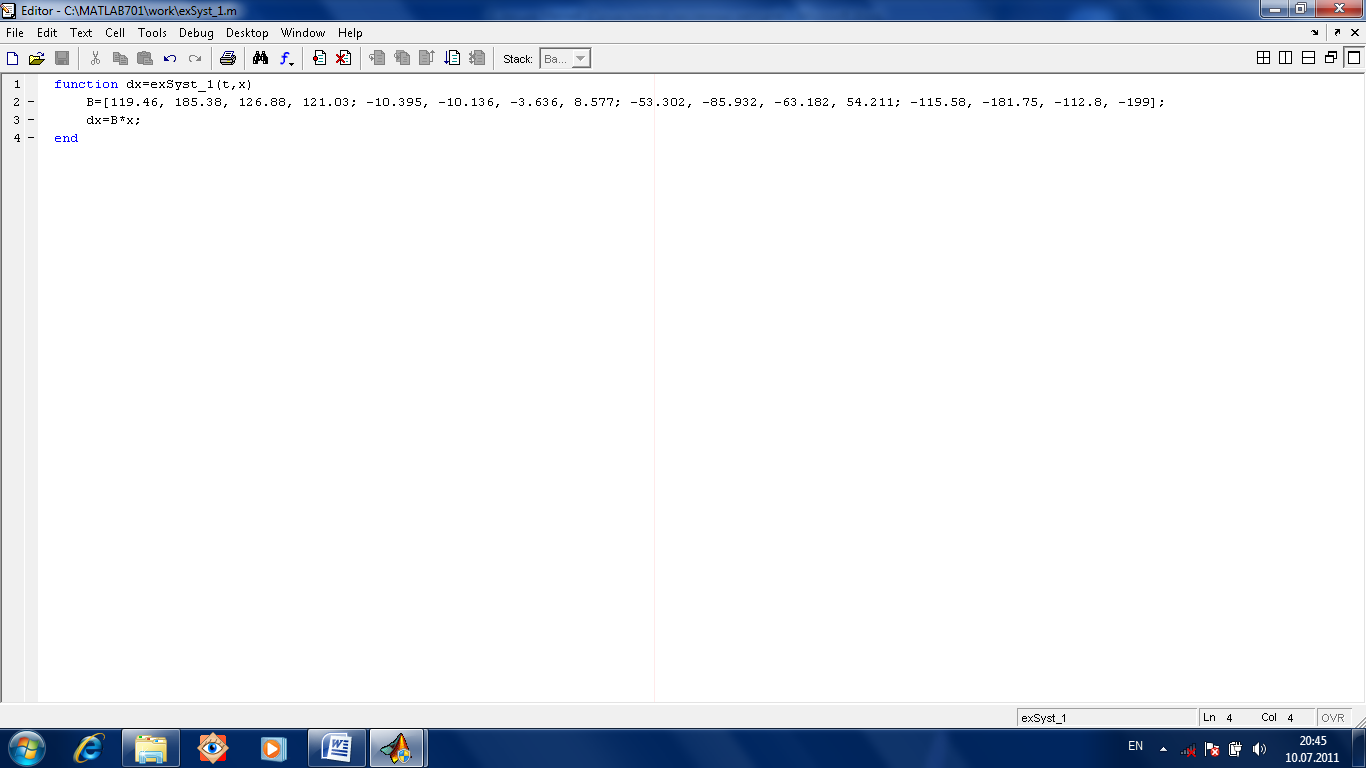
Имеющей начальное условие X(0)=(1 1 1 1);
Сначала
проверим, является ли матрица В матрицей
жесткой системы. Оператор eig(B)
возвращает собственные числа матрицы.
Одно из них неотрицательное, то есть
условие соблюдено не полностью. Далее
находим число жесткости s=28,
что не очень много, то есть система не
очень жесткая. Затем команда ode15s
решает задачу. Возвращается вектор Т и
матрица Х, число столбцов в которой
равно числу переменных. 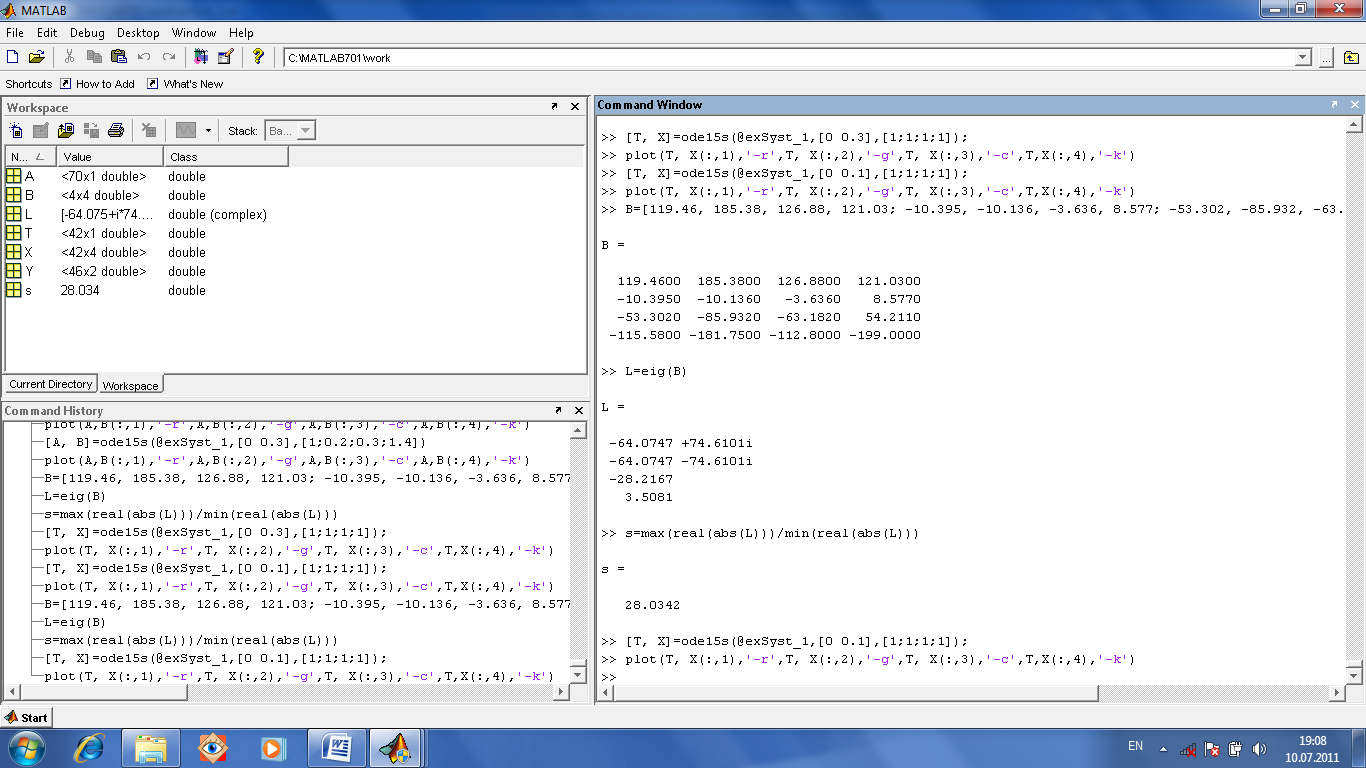
![]()
Строим
график. На нем видно, что корни изменяются
в зависимости от параметра Т как бы
синусоидально. Такой характер изменений
корней характерен для жестких систем.
По мере роста числа жесткости, корни
колеблются (в зависимости от параметра
Т) все более резко, образуя «детский
рисунок» на экране.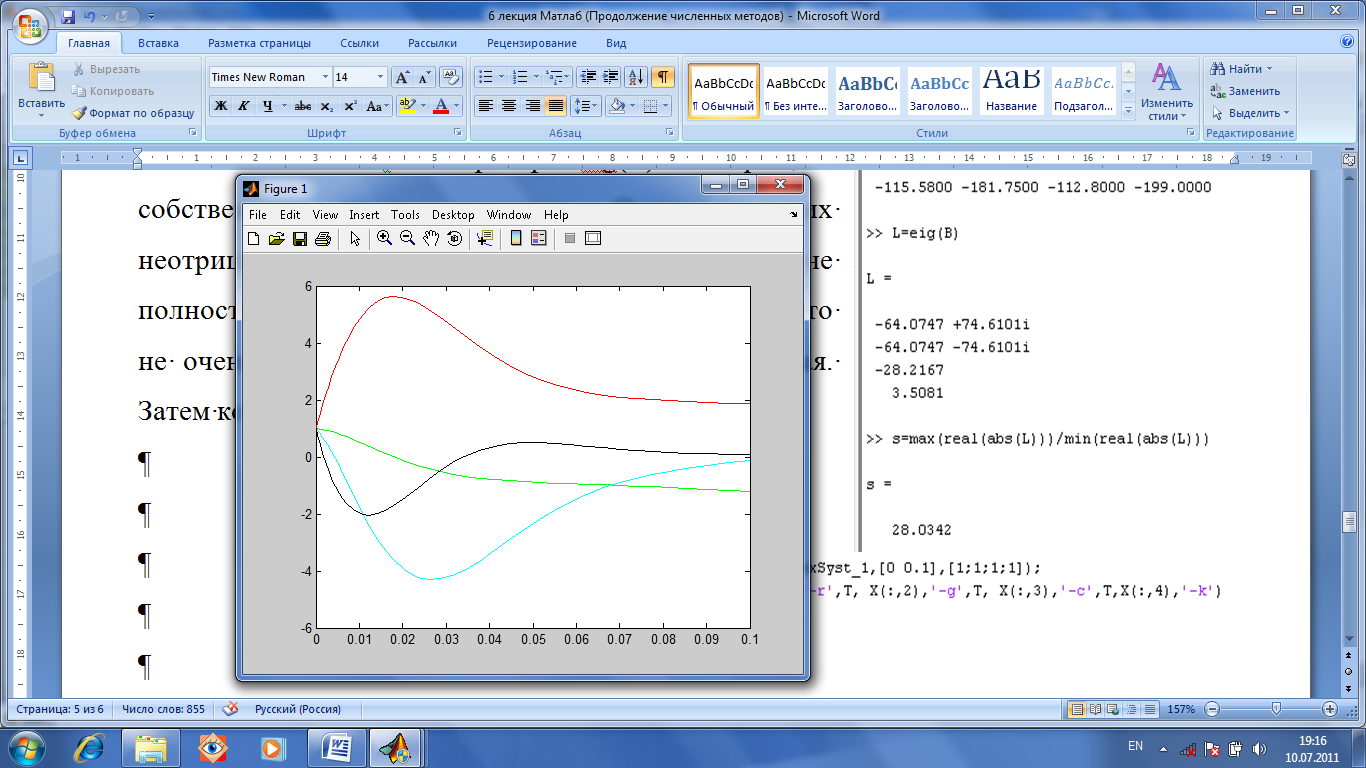
Решение дифференциальных уравнений высших порядков. Если в уравнении есть производные высших порядков, то действуем преобразуя уравнение с понижением степени производной, но с увеличением числа переменных.
Решим
краевую задачу. d2x/dt2+4dx/dt+13x=esin
t
при x(0.25)=-1,
x/(0.25)=1
на интервале [0.25; 2]. Преобразуем следующим
образом. Пусть y=dx/dt.
Тогда получим систему уравнений.
dy/dt=-4y-13x+esin
t
с начальными условиями y(0.25)=1,
x(0.25)=-1;
dx/dt=y
Для
ее решения воспользуемся функцией
ode45.
Ей передадим имя М-функции для вышеописанной
системы, интервал изменения
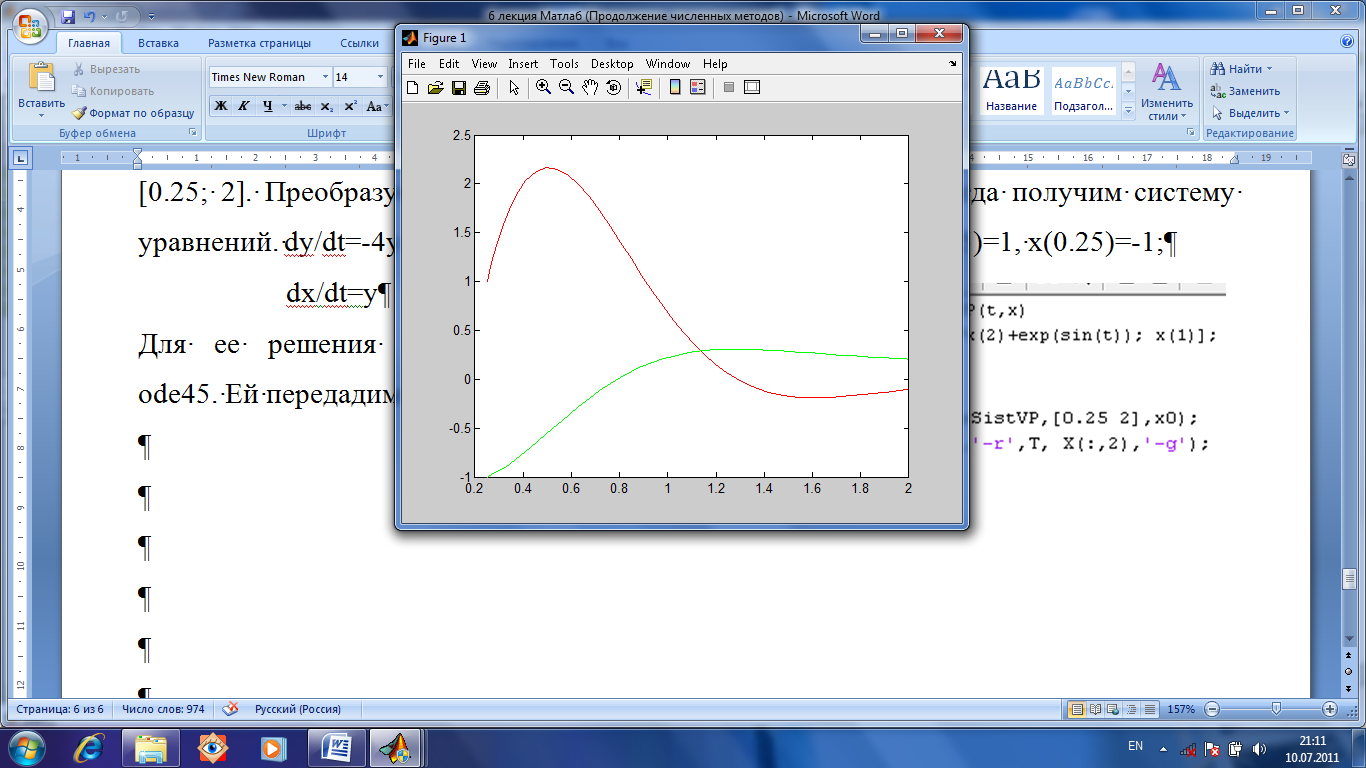
параметра Т, вектор х0 начальных условий для
переменных.
Функция ode45 вернет нам матрицу для Х и вектор для Т. Построим график.
Обработка результатов эксперимента методом наименьших квадратов.
Построение
полиномиальной зависимости.
Для этого есть функция polyfit,
которой передаются массив абсцисс,
массив ординат (экспериментальных
точек) и степень полинома, который
требуется получить так, чтобы он описывал
экспериментальную зависимость массива
ординат от массива абсцисс. Функция
возвращает вектор коэффициентов
вышеупомянутого полинома. 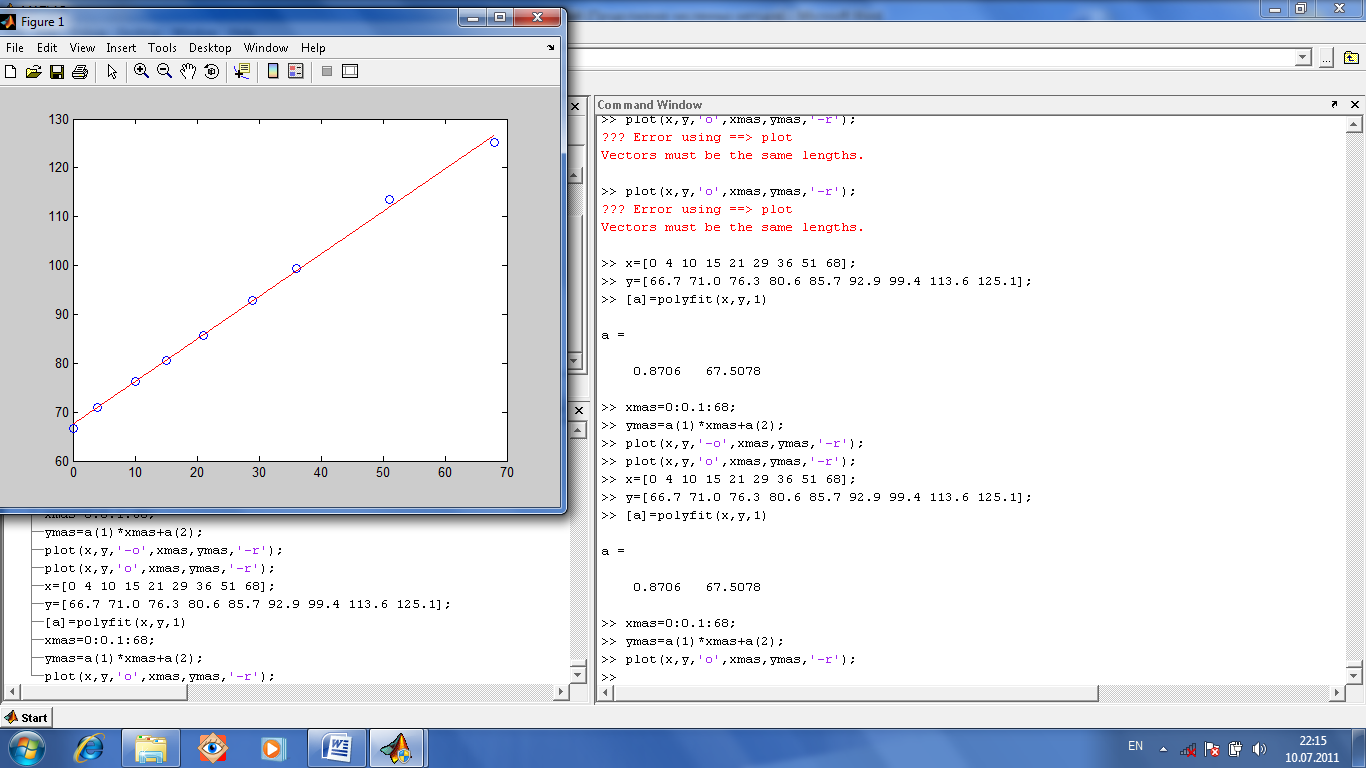
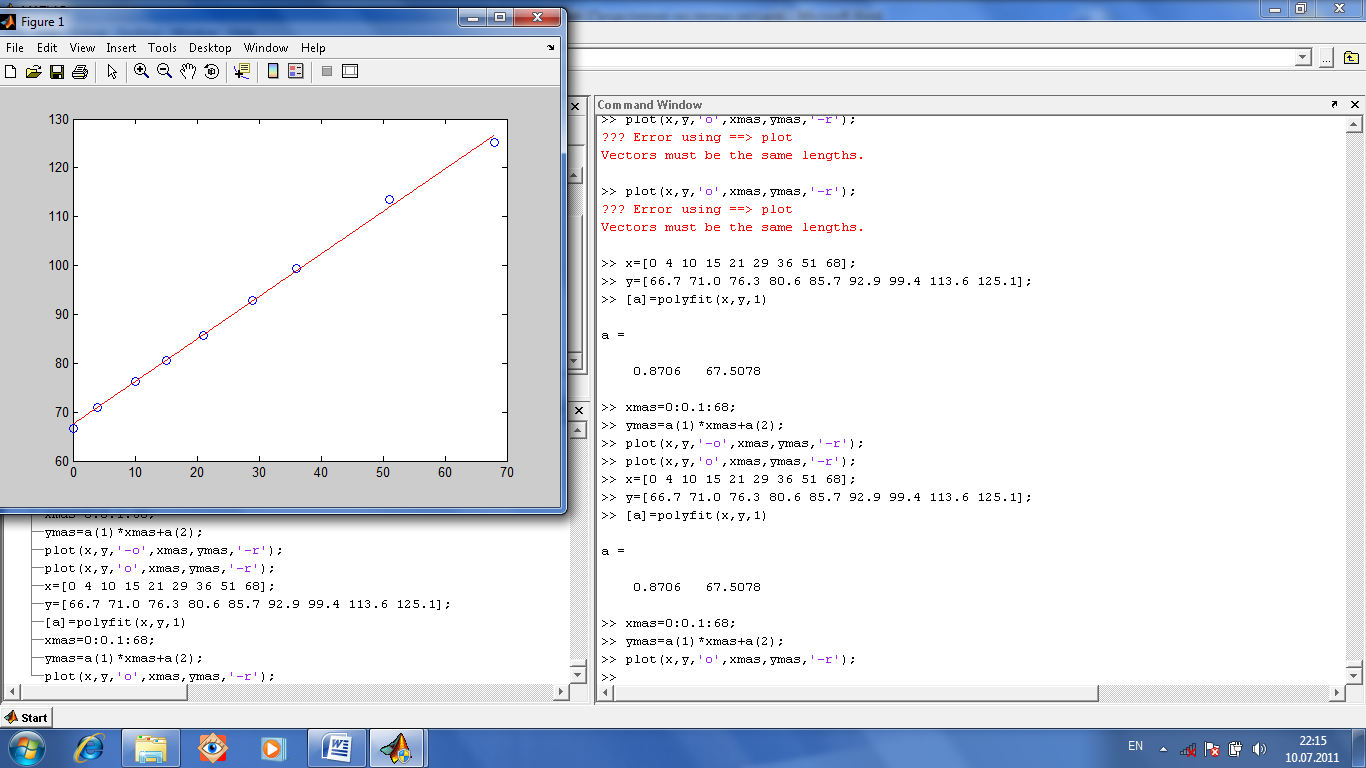
Зная коэффициенты полинома, можно функцией polyval вычислить значение полинома при любом значении его аргумента (то есть получить сплошную расчетную кривую, проходящую через отдельно расположенные экспериментальные точки).
Если
же требуется подобрать такую зависимость,
которая не содержит некоторые степени
(например, y=3x5+6x3+x+65)
то тем самым требуется найти минимум
функции. Поясним это на примере. Пусть
требуется функция вида y=c1+c2x2+c3x3,
тогда, используя функцию fminsearch(‘fname’,c)
получим вектор коэффициентов. Однако
в функцию fminsearch
следует передавать не вышеописанную
функцию у(х), а переделанный ее вариант
вида yiexperimental-(c1+c2xi2+c3xi3).
Тогда минимум функции будет достигнут
в случае, если вычисленные ее значения
практически совпадают с экспериментальными,
то есть идеально описывают экспериментальные
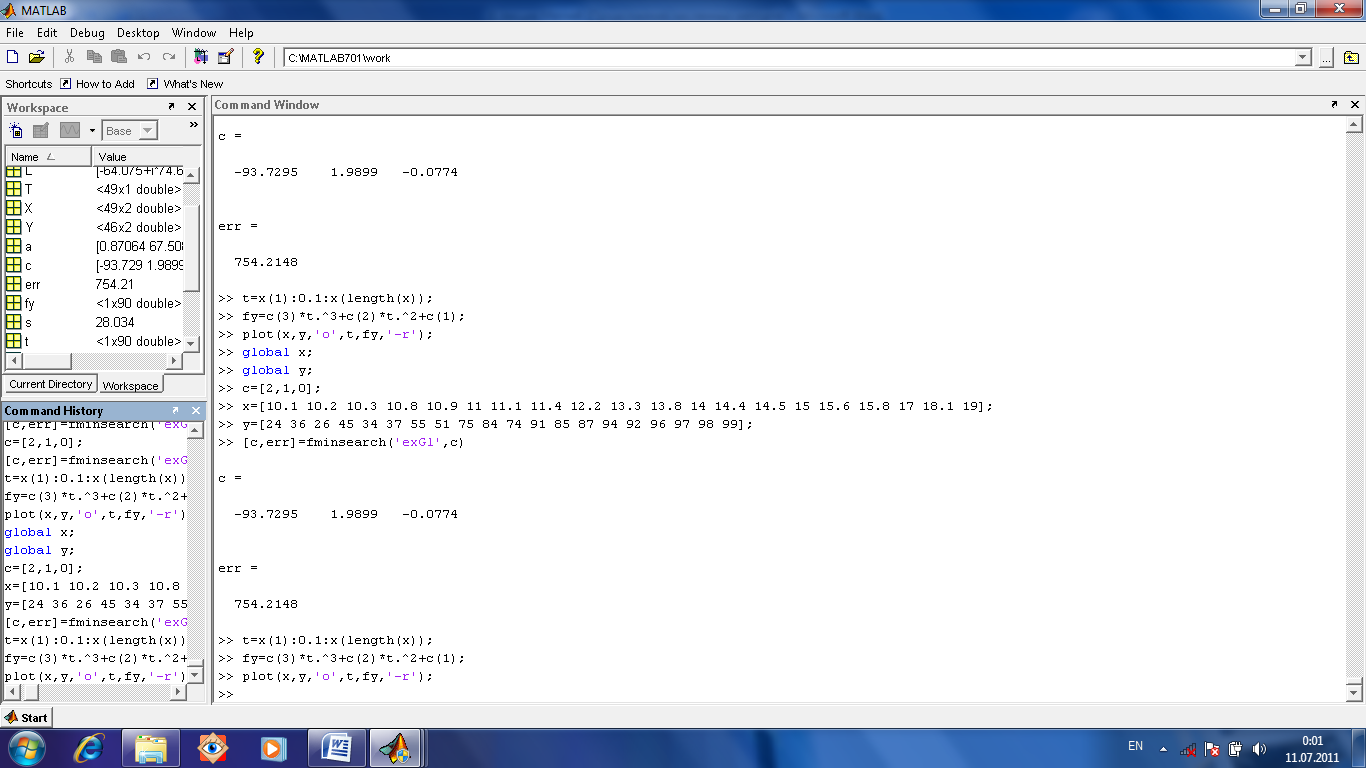
данные. 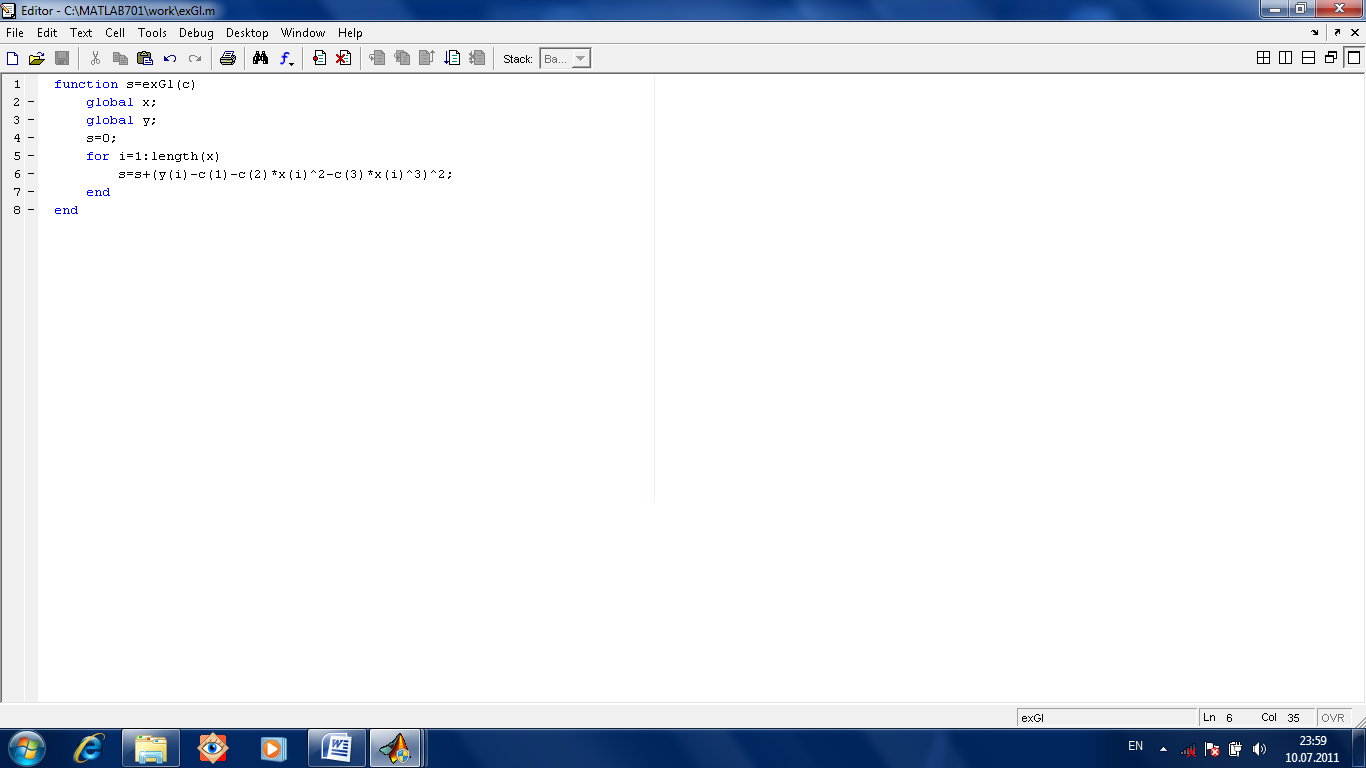
![]()
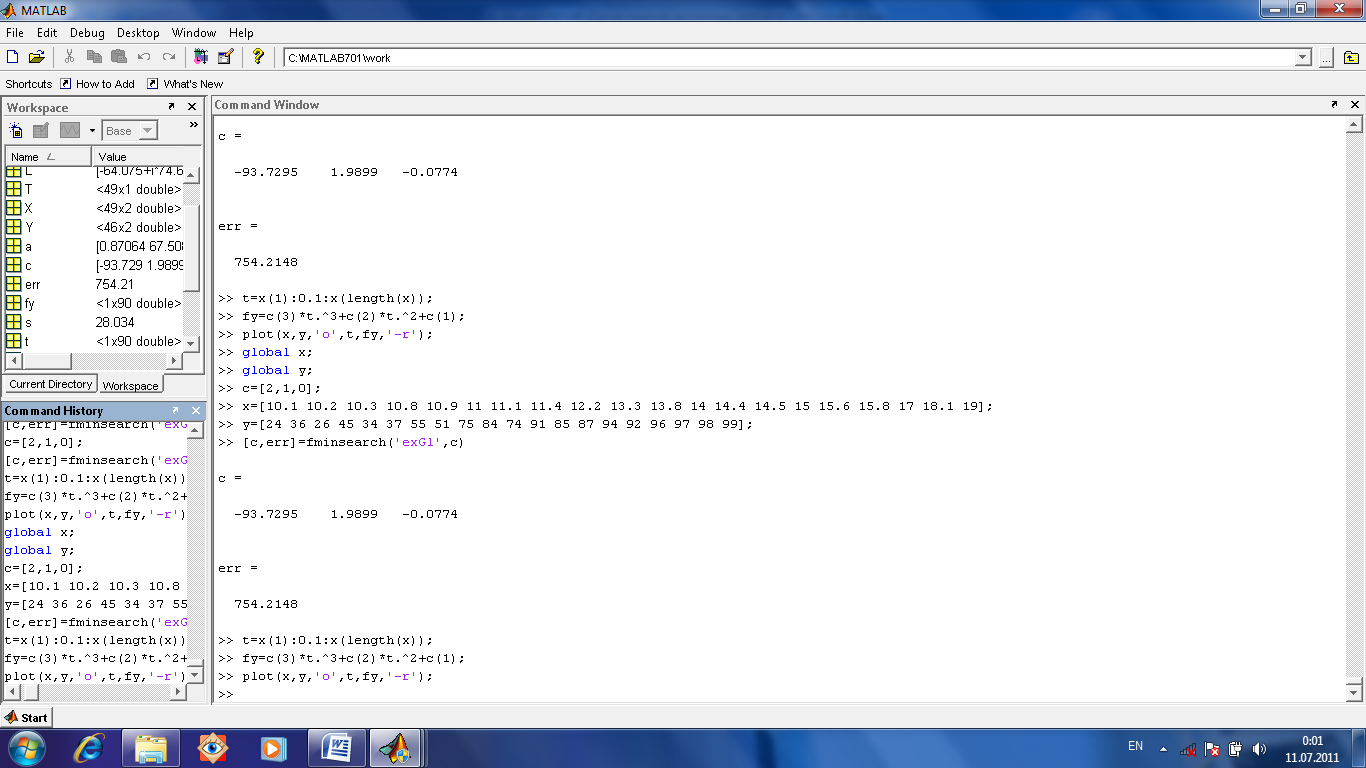
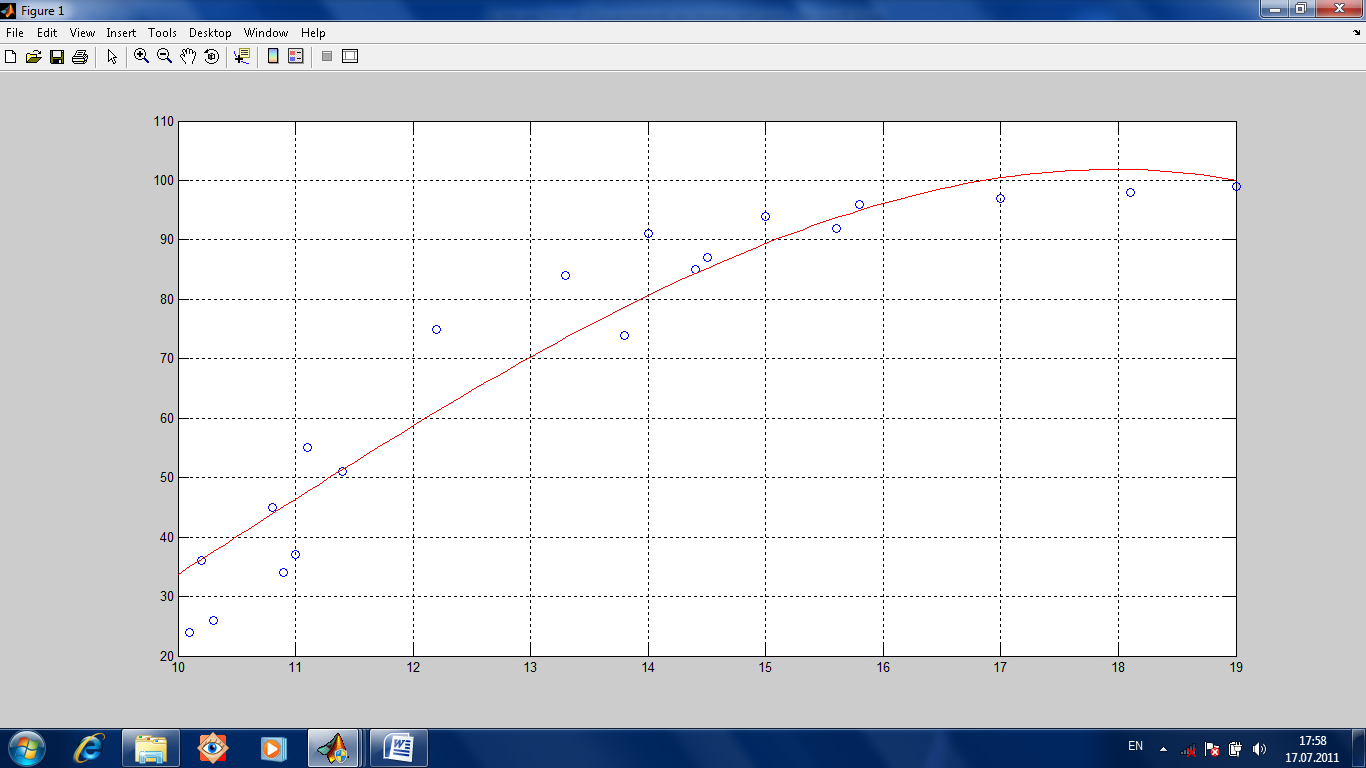
Сначала определяем вектор предполагаемых приблизительно значений с (если его неудачно выбрать то ответ не получится). Потом объявляем переменные х и у глобальными. Затем вводим экспериментальные данные. После этого запускаем функцию fminsearch. Полученный от нее вектор значений с используем для построения расчетной кривой. Потом сравниваем, насколько кривая идет через экспериментальные точки.
Интерполяция
функций.
Для реализации сплайн-интерполяции
используется функция yi=interp1(x,y,xi,method)
где х массив абсцисс, у массив ординат
(экспериментальных точек), xi
точки в которых необходимо вычислить
значение с помощью сплайна, yi
функция в этих точках. 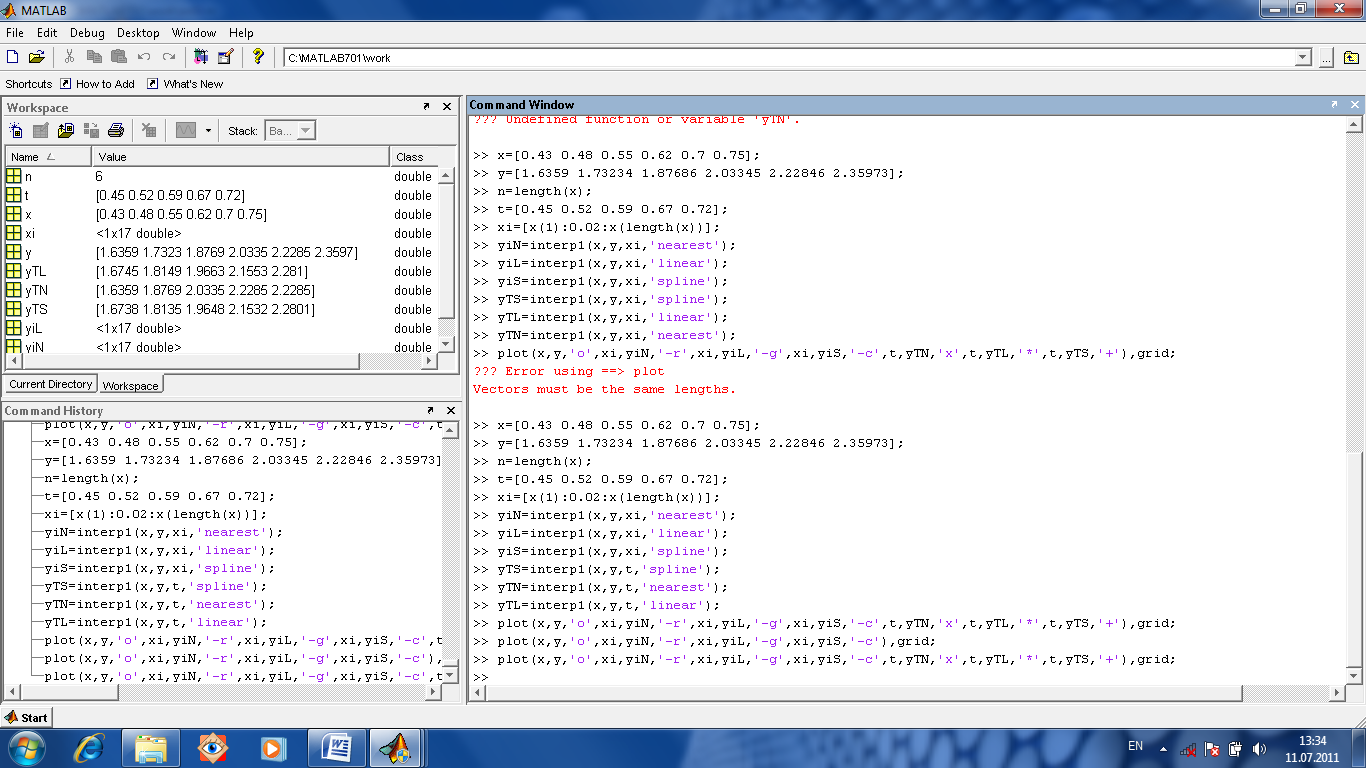
В
зависимости от используемых методов,
получаются различные результаты. Для
уплотнения экспериментальных точек,
создан массив xi
из точек с одинаковым шагом, и для них
будут найдены значения функции y(x).
Кроме того, создан массив из точек t
и эти точки расположены между
экспериментальными. Для них тоже будут
найдены значения функции y(t).![]()
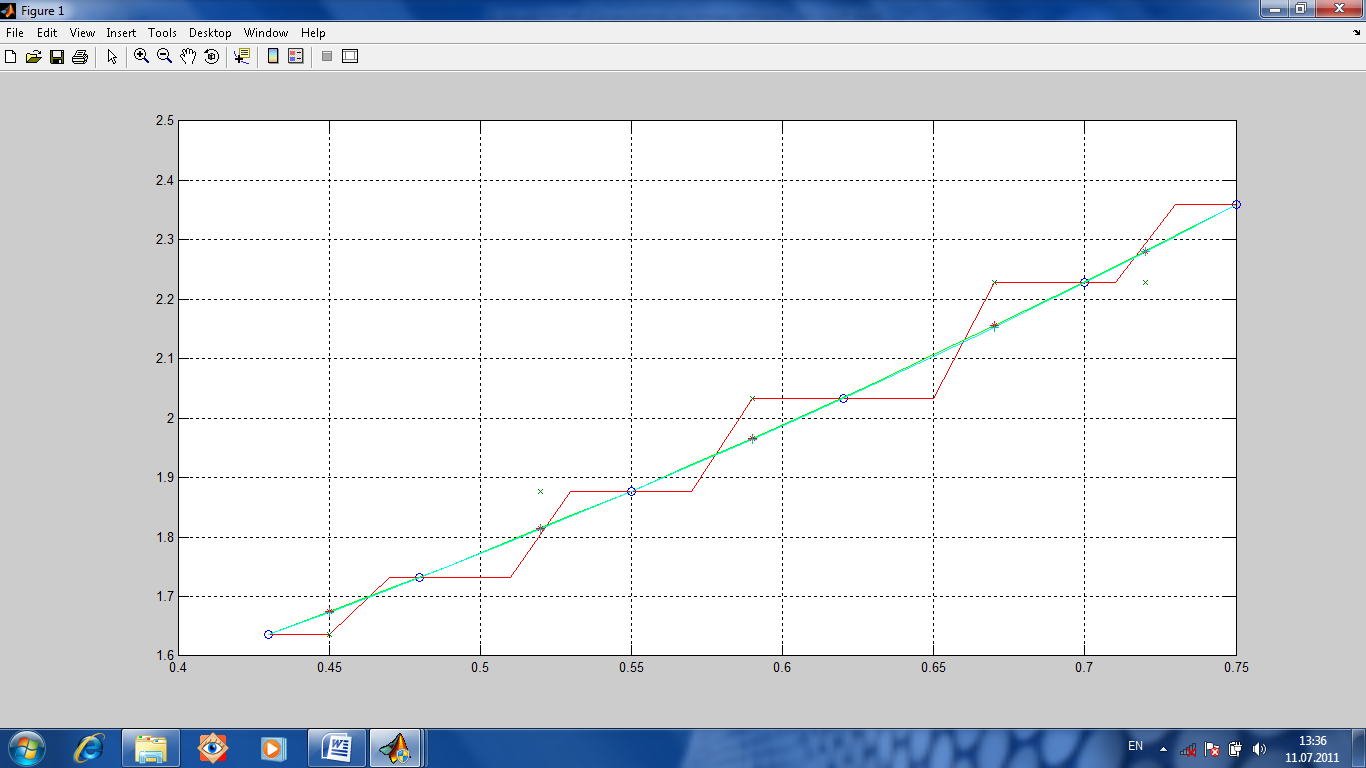
linear линейная интерполяция; spline кубический сплайн; nearest интерполяция по соседним точкам (значение равно значению в ближайшей узловой точке).
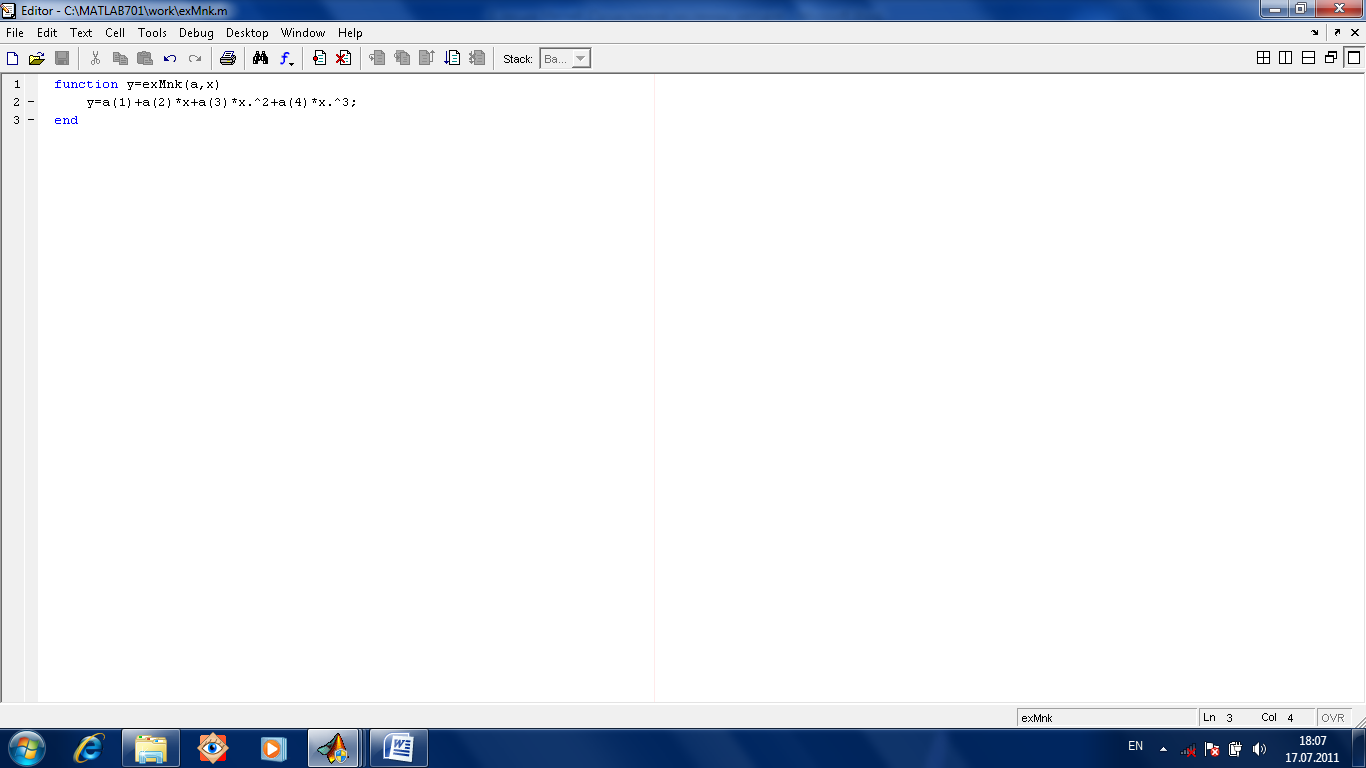
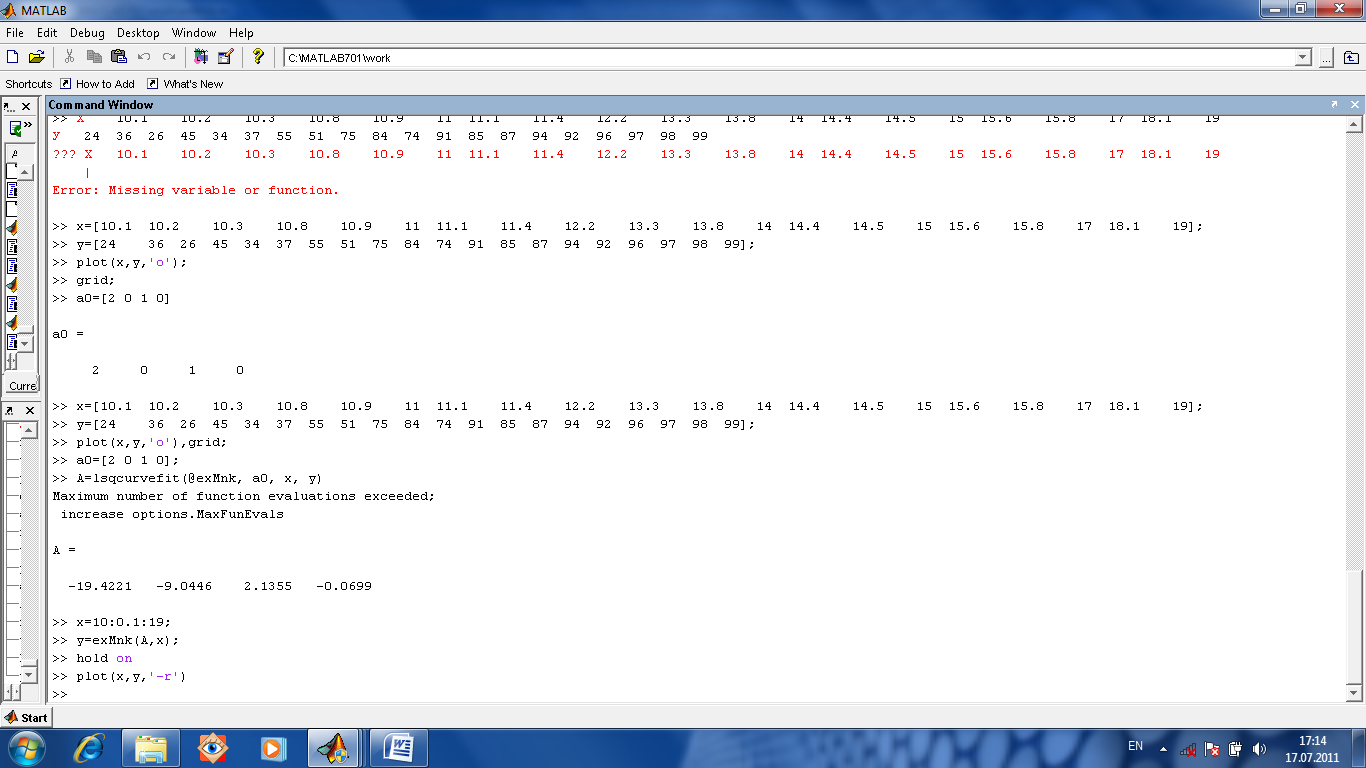
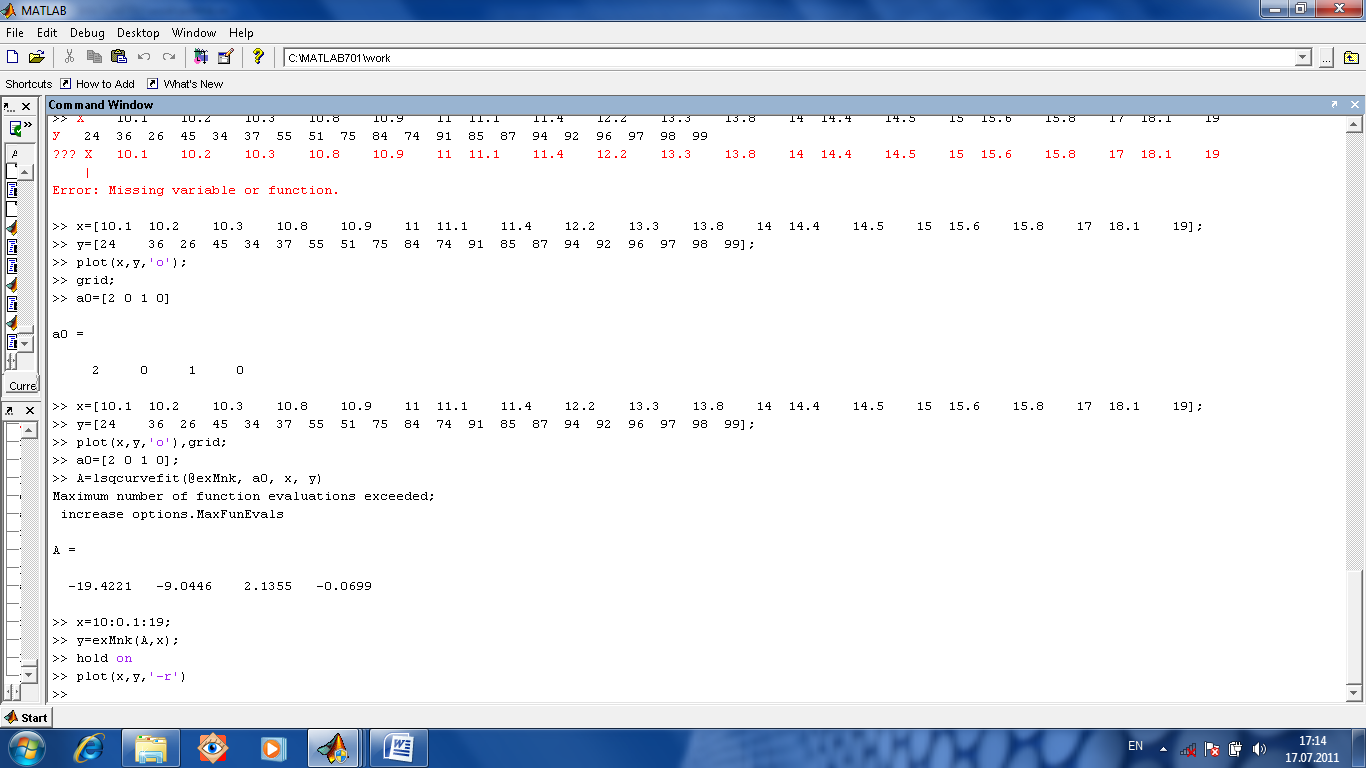
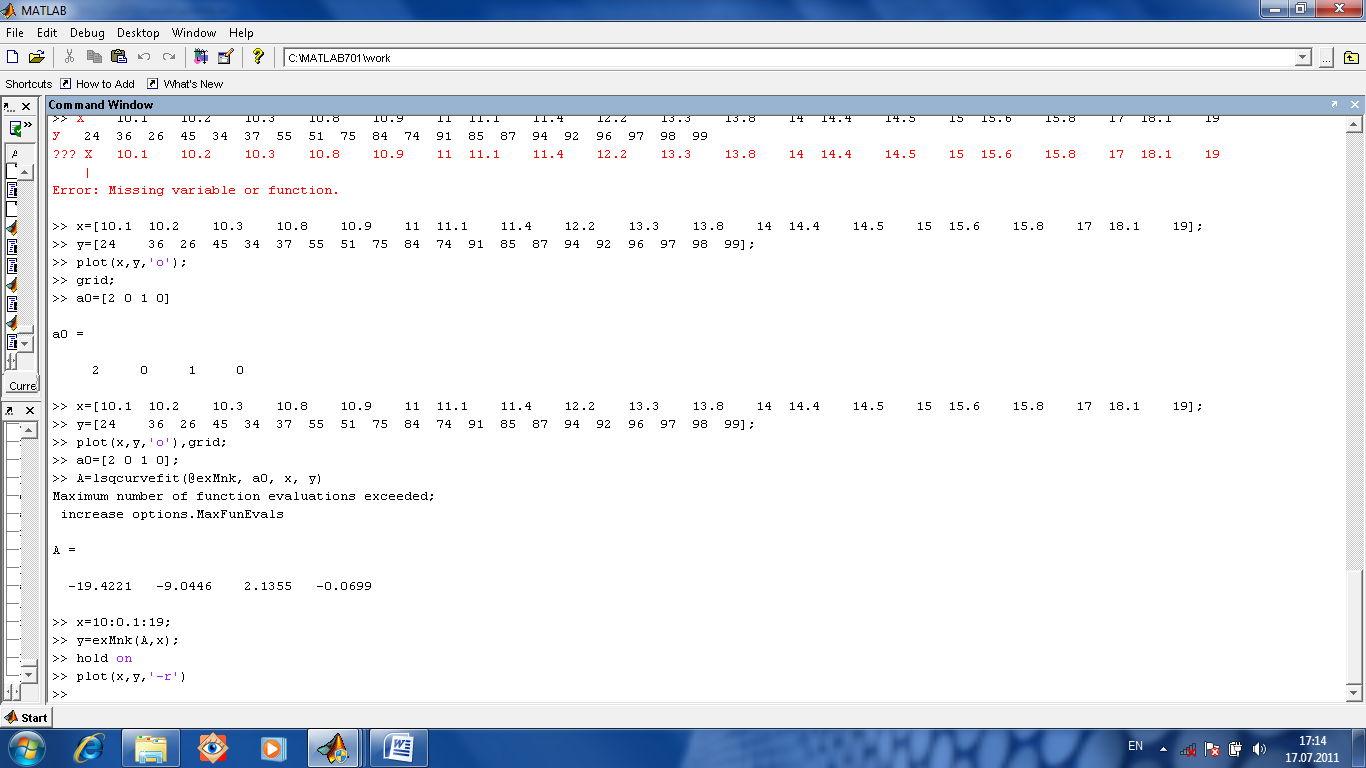
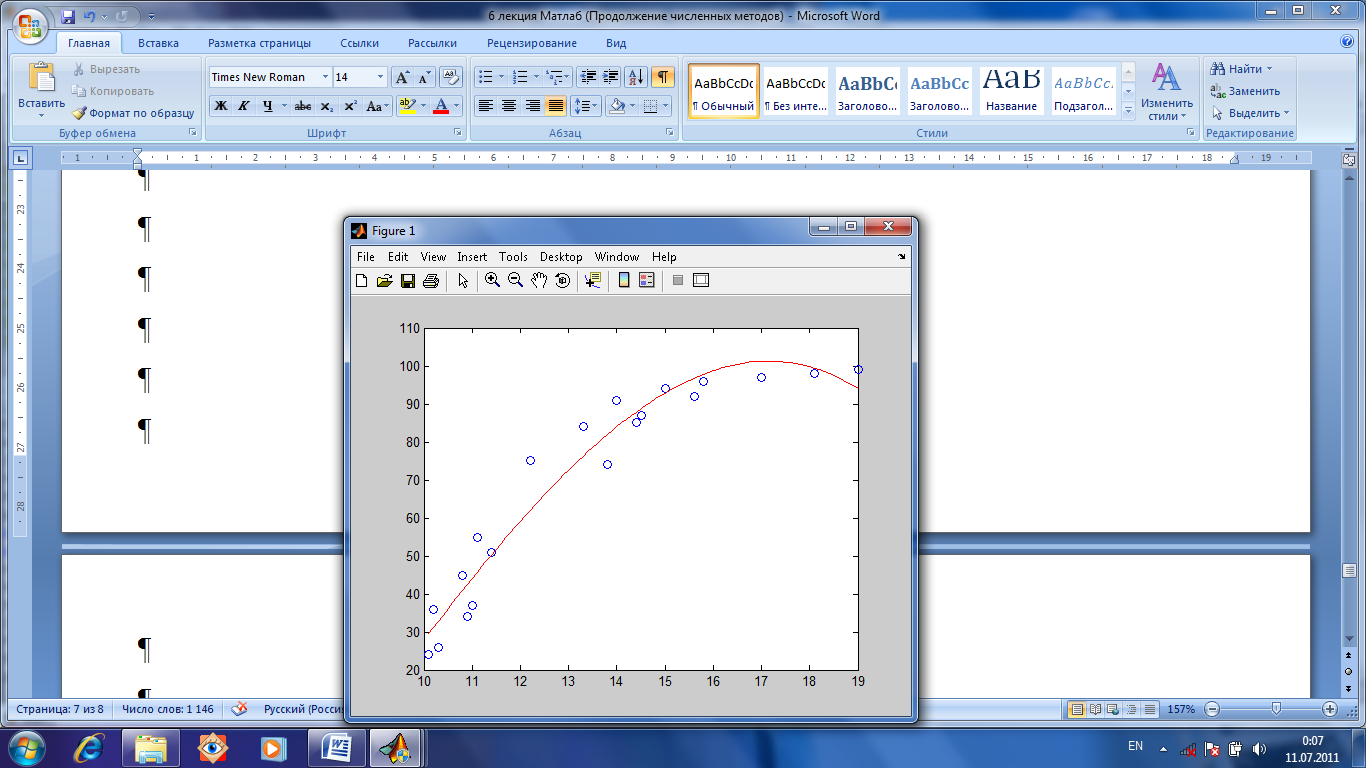
Подбор параметров. Для подбора параметров предназначена функция [res]=lsqcurvefit(fun, a0, x, y, Lx, Rx), где fun имя М-функции, вычисляющей левую часть выражения вида y=f(x, a0, a1, …, ak), параметры которой a0, a1, …, ak неизвестны и их-то и надо найти. Они перечислены в векторе возвращаемых значений res. а0 начальное приближение параметров. x, y экспериментальные данные. Lx, Rx ограничения на параметры вида Lx≤x≤Rx, Lx≤x, x≤Rx.
Пусть, для примера, надо подобрать параметры функции y=a1+a2x+a3x2+a4x3. Пусть даны экспериментальные данные.
|
Х |
10.1 |
10.2 |
10.3 |
10.8 |
10.9 |
11 |
11.1 |
11.4 |
12.2 |
13.3 |
13.8 |
14 |
14.4 |
14.5 |
15 |
15.6 |
15.8 |
17 |
18.1 |
19 |
|
У |
24 |
36 |
26 |
45 |
34 |
37 |
55 |
51 |
75 |
84 |
74 |
91 |
85 |
87 |
94 |
92 |
96 |
97 |
98 |
99 |
Выберем вектор начальных приближений а0=(2, 0, 1,0).