План семестра поурочный по ВычМат-2014 / Занятие-11-Многомерн-Оптимизация / 9 лекция Матлаб (Оптимизация, линейное программирование)

МАТЛАБ. ОПТИМИЗАЦИЯ, ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

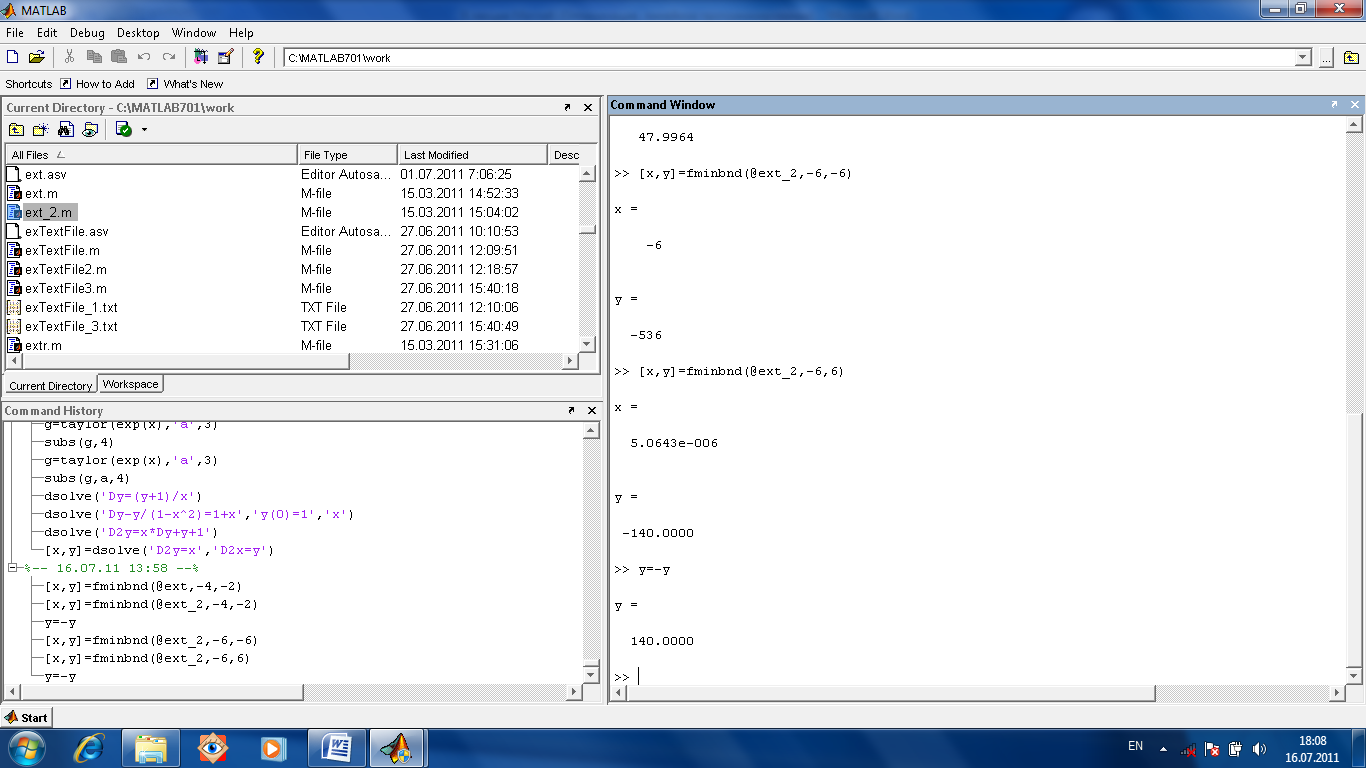
Поиск экстремума функции одной переменной. Поиск локального (в пределах определенного интервала) минимума осуществляет функция [x,y]=fminbnd(имяФункции,границыИнтервала). Если же надо найти локальный минимум, то исследуемую функцию берут с другим знаком и ищут ее минимум, который фактически является ее максимумом. При этом значение функции в максимуме это найденное значение с другим знаком.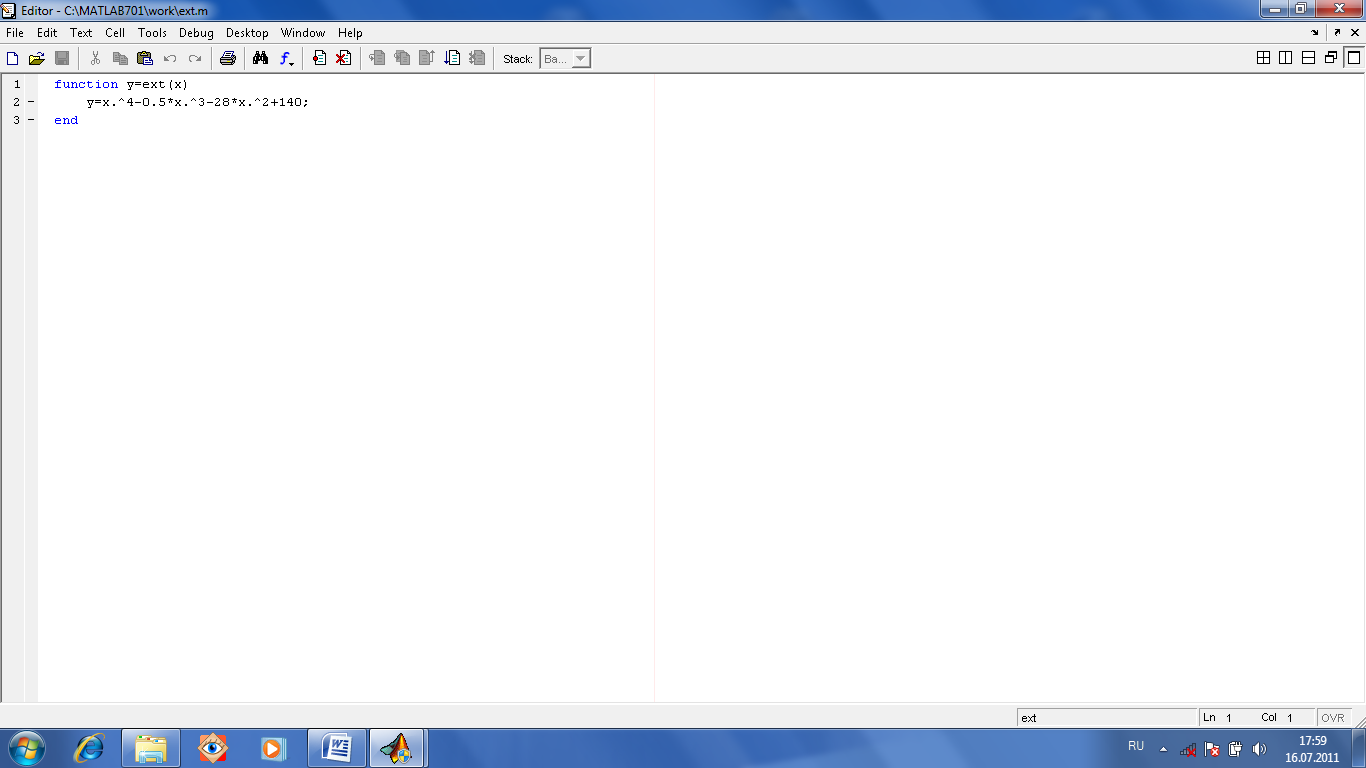

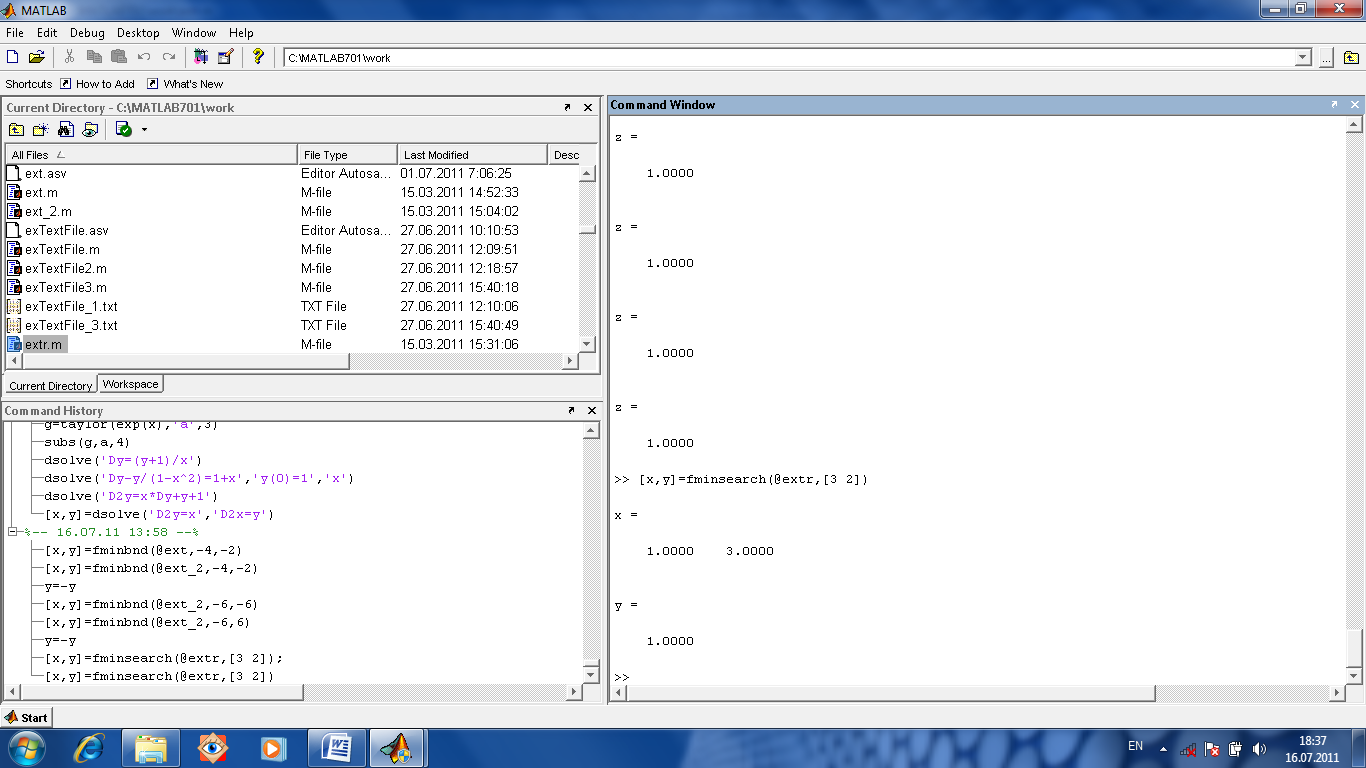
Поиск экстремума функции нескольких переменных. Если функция вычисляется от нескольких переменных, то для поиска ее минимума используется (после приблизительной оценки начальных приближений переменных в предполагаемом минимуме) команда [x,y]=fminsearch(имяФункции, векторНачальныхПриближенийПеременных).

Решение задач линейного программирования. В задачах линейного программирования требуется найти максимум или минимум линейной функции многих переменных при линейных ограничениях в виде равенств или неравенств. Рассмотрим для примера такую задачу.

Пусть функция L(x₁,x₂,x₃,x₄)=x₁+x₂+x₃+x₄ и надо найти ее максимум и соответствующие ее максимуму значения переменных.

Пусть даны ограничения в виде неравенств. x₁≥0, x₂≥0, x₃≥0, x₄≥0.

Пусть также даны еще ограничения в виде неравенств.

3x₁-x₂≤7, x₂-2x₃≤-1, 4x₃-x₄≤3, 5x₁+2x₄≥14.

Для решения задачи линейного программирования (нахождения минимума) используется функция [x, L, f]=linprog(c, A, b, A1, b1,Lx, Rx) где

x вектор значений переменных, полученный в качестве ответа; L значение функции в минимуме;

f параметр, характеризующий вычислительный процесс (если он ноль то решение приостановлено после достижения максимального числа итераций, если положителен то все нормально решено, если отрицателен то решения не найдено);

c функция цели представленная в виде вектора коэффициентов (в нашем случае [1 1 1 -1] но так как нам нужен максимум, а функция [x, L, f]=linprog(c, A, b, A1, b1, Lx, Rx) ищет минимум, то в выражении для функции поменяем знак, поэтому вектор коэффициентов будет [-1 -1 -1 1]);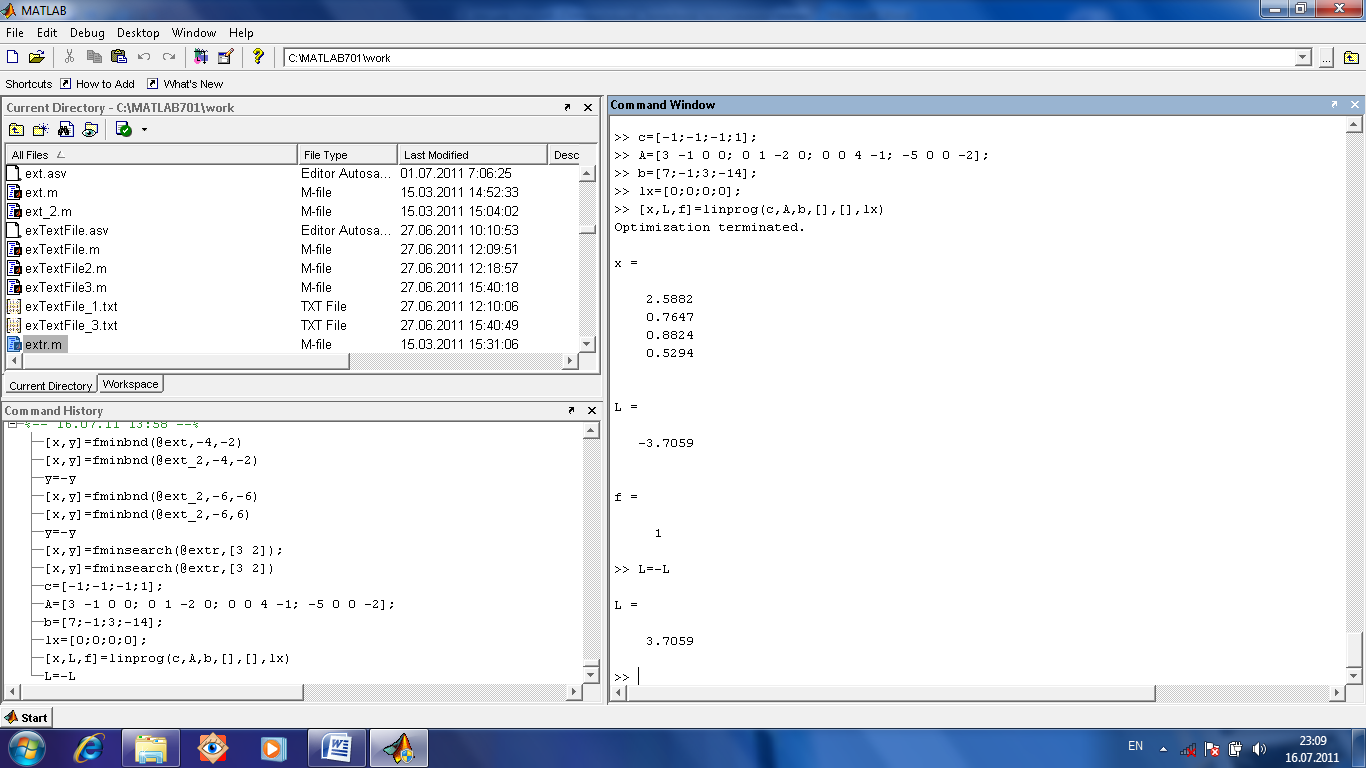

A, b система ограничений, заданная в матричном виде Ax≤b (это в нашей задаче ограничения 3x₁-x₂≤7, x₂-2x₃≤-1, 4x₃-x₄≤3, 5x₁+2x₄≥14, но так как 5x₁+2x₄≥14 не подходит, то надо поменять знак в этом неравенстве и тогда оно будет -5x₁-2x₄≤-14, в таком случае матрица А состоит из коэффициентов (при переменных) в этих неравенствах, а столбец b состоит из правых (не содержащих переменных) частей неравенств;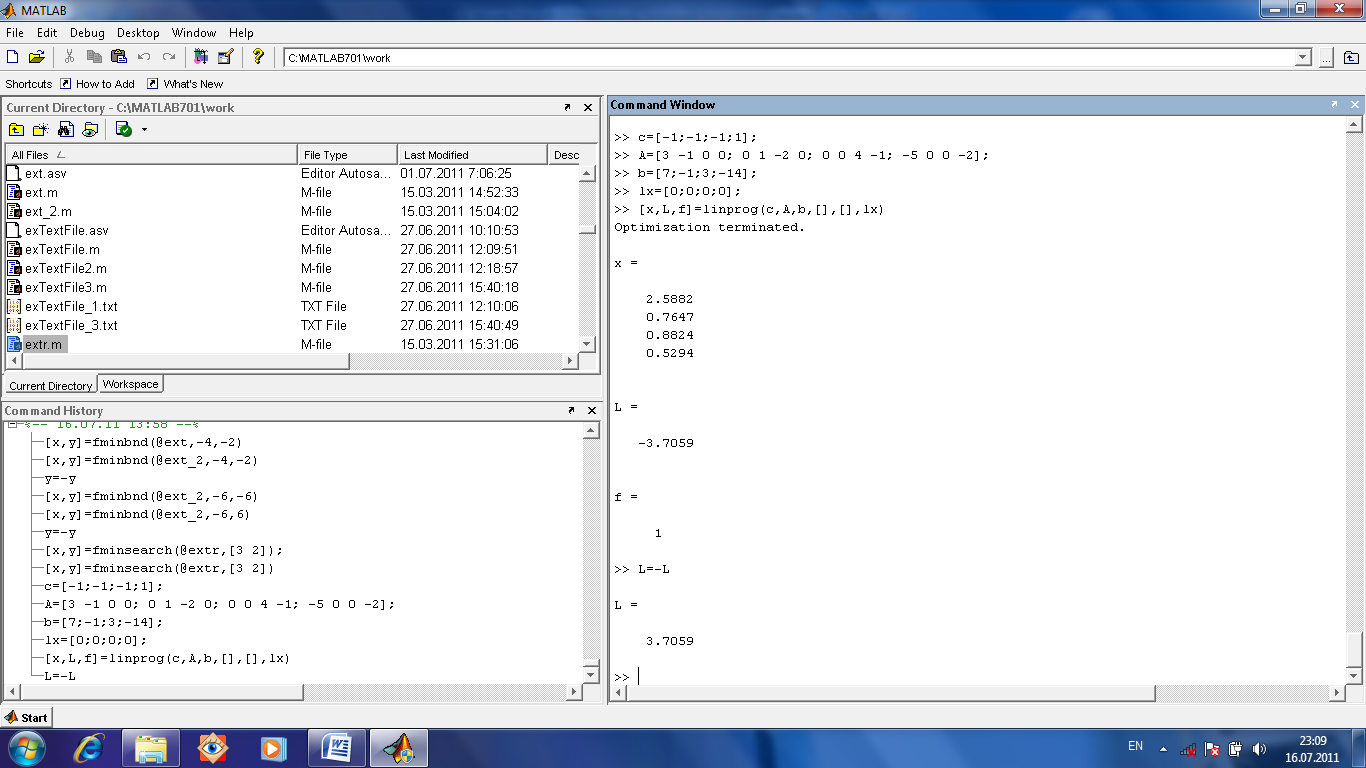

A1, b1 система равенств вида A1x=b (в нашей задаче такой системы ограничений нету, но могла бы быть);

Lx, Rx относятся к ограничениям в виде Lx≤x≤Rx, Lx≤x, x≤Rx (в нашей задаче есть ограничения вида Lx≤x, поэтому вектор Lx будет 0 0 0 0).

При использовании функции linprog в списке аргументов вместо тех, которые не указаны, ставятся пустые квадратные скобки.

Рассмотрим еще пример для тренировки. Пусть дана функция W=x₁+x₂+3x₃-x₄ и надо найти ее максимум. Пусть даны ограничения в виде неравенств.

x₁-5x₂+4x₃≤5, x₁-2x₂-3x₃≤4, x₁+6x₂+5x₃≤4, x₂+x₃≤1. И пусть есть еще ограничения в виде неравенств. x₁≥0, x₂≥0, x₃≥0, x₄≥0.

Решим задачу с помощью функции [x, L, f]=linprog(c, A, b, A1, b1, Lx, Rx). Для ее применения нам надо подготовить аргументы функции. Вектор с коэффициентов функции равен (1 1 3 -1), но так как функция linprog ищет минимум, а нам нужен максимум, то поменяем знак у коэффициентов функции и тогда вектор с будет (-1 -1 -3 1). Матрица А состоит из коэффициентов при переменных в системе неравенств x₁-5x₂+4x₃≤5, x₁-2x₂-3x₃≤4, x₁+6x₂+5x₃≤4, x₂+x₃≤1. Так как все они со знаком ≤ то ничего менять не требуется. Вектор b состоит из правых частей этих же неравенств. Матрица A1 из системы A1х=b1 для нас не актуальна (нет таких условий). Lx, Rx относятся к ограничениям в виде Lx≤x≤Rx, Lx≤x, x≤Rx. У нас есть ограничения в виде неравенств. x₁≥0, x₂≥0, x₃≥0, x₄≥0. Тогда вектор Lx=[0; 0; 0; 0]. Что касается остальных типов ограничений, то так как у нас нет таких ограничений, то для нас они не важны.

Задачи нелинейного программирования. Нелинейная задача отличается от линейной. В ней есть система линейных неравенств Ax≤b, система линейных равенств A1x=b1, система ограничений вида lx≤x≤rx, lx≤x, x≤rx. Однако помимо этих уже знакомых (из линейного программирования) условий, есть еще система нелинейных ограничений вида g1(x)≤0, и система нелинейных равенств g2(x)=0. Для решения задачи нелинейного программирования (после выбора вектора начальных приближений х0) используется функция [x, y, f]=fmincon(F, x0, A, b, A1, b1, Lx, Rx, G), где G это М-функция, вычисляющая левые части нелинейных ограничений g1(x)≤0, g2(x)=0. Если какие-то аргументы не определены, то вместо них в вызове функции ставятся квадратные скобки.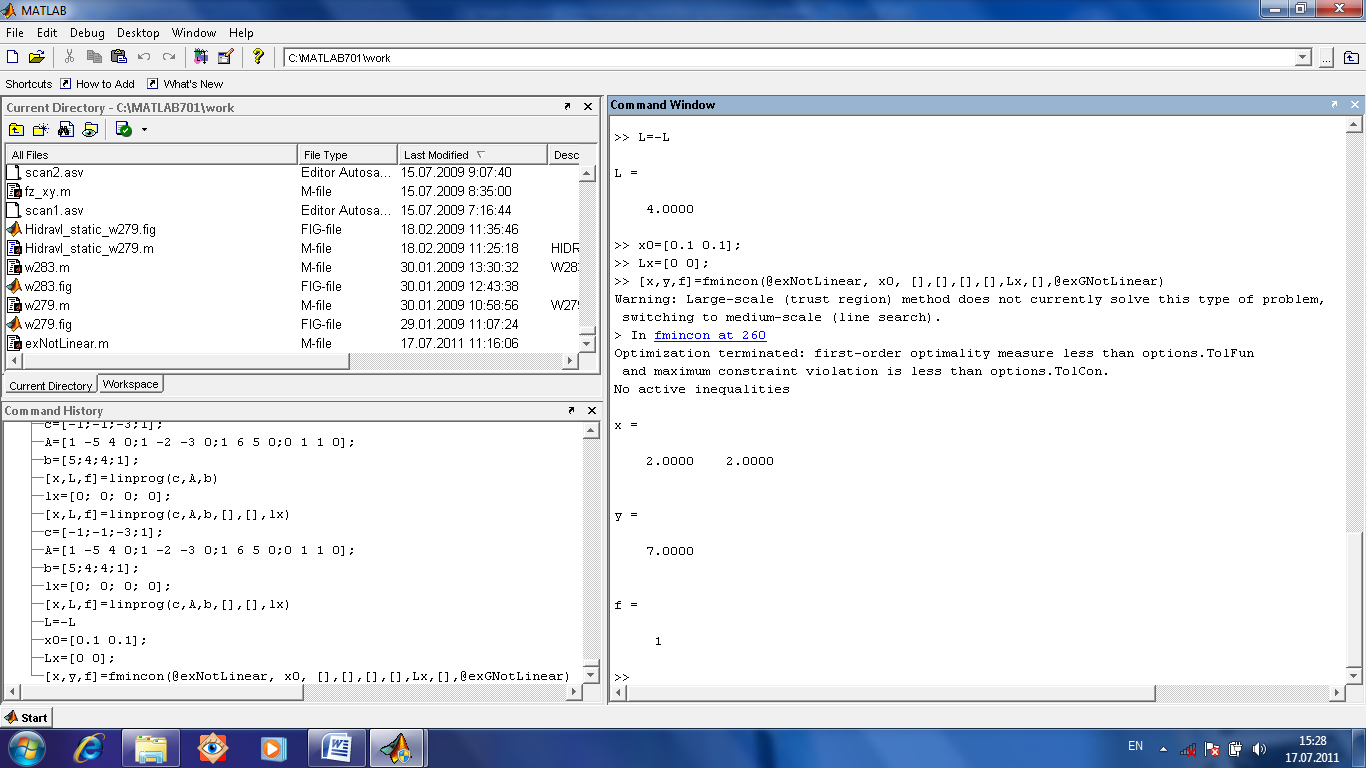

Рассмотрим для примера следующую задачу. пусть дана функция x₁²+x₂²=1 при условии, что x₁x₂=4, x₁≥0, x₂≥0. Вектор начальных приближений примем равным х0=(0.1, 0.1).