
Задание с 04_16
.docxДЗ8: «НЕКОТОРЫЕ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН»
-
Найти среднее число лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, а вероятность выигрыша одного билета равна 0,1. Найти дисперсию числа успехов в данном опыте.
-
Проверяется партия из 10000 изделий. Вероятность того, что изделие окажется бракованным, равна 0,002. Найти математическое ожидание и дисперсию числа бракованных изделий этой партии. Найти вероятность того, что в партии есть хотя бы одно бракованное изделие.
-
Производится стрельба по цели до первого попадания. Вероятность попадания при каждом выстреле равна 0,2. Найти математическое ожидание и дисперсию числа произведенных выстрелов, считая, что:
А) стрелять можно неограниченное число раз;
Б) в наличии есть всего 5 патронов.
-
Игральная кость подбрасывается до первого появления пяти очков. Какова вероятность того, что первое выпадение пятерки произойдет при пятом подбрасывании игральной кости?
-
Некто ожидает телефонный звонок между 19:00 и 20:00. Время ожидания звонка есть непрерывная сл.в.
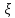 ,
имеющая равномерное распределение на
отрезке
,
имеющая равномерное распределение на
отрезке
 .
Найти вероятность того, что звонок
поступит в промежутке от 19 ч. 22 мин. до
19 ч. 46 мин.
.
Найти вероятность того, что звонок
поступит в промежутке от 19 ч. 22 мин. до
19 ч. 46 мин. -
Про сл.в.
 известно, что она равномерно распределена
на отрезке
известно, что она равномерно распределена
на отрезке
 .
Найти:
.
Найти:
А)
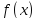 ; Б)
; Б)
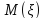 и
и
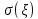 ; В)
; В)
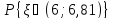 .
.
-
Сл.в.
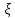 распределена по показательному закону
с параметром
распределена по показательному закону
с параметром
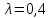 .
Найти плотность и функцию распределения
вероятностей (
.
Найти плотность и функцию распределения
вероятностей ( ),
),
 ,
а также вероятность попаданий значений
сл.в.
,
а также вероятность попаданий значений
сл.в.
 в интервал
в интервал
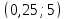 .
. -
Время
 выхода из строя радиостанции подчинено
показательному закону распределения
с плотностью
выхода из строя радиостанции подчинено
показательному закону распределения
с плотностью
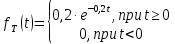 .
.
Найти: функцию распределения
 ,
математическое ожидание и дисперсию
сл.в.
,
математическое ожидание и дисперсию
сл.в.
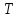 ,
вероятность того, что радиостанция
сохранит работоспособность от 1 до 5
часов работы.
,
вероятность того, что радиостанция
сохранит работоспособность от 1 до 5
часов работы.
-
Определить закон распределения сл.в.
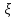 ,
если ее плотность вероятности имеет
вид
,
если ее плотность вероятности имеет
вид
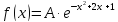 .
.
Найти:
А)
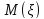 ;
Б)
;
Б)
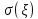 ; В)
значение коэффициента
; В)
значение коэффициента
 ; Г)
; Г)
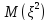 ; Д)
; Д)
 ,
,
Е) вероятность того, что эта сл.в. три
раза из пяти примет значение, попадающее
в интервал
 .
.
-
Случайные ошибки измерения детали подчинены нормальному закону с параметром
 мм. Найти вероятность того, что измерение
детали произведено с ошибкой, не
превосходящей по модулю 25 мм.
мм. Найти вероятность того, что измерение
детали произведено с ошибкой, не
превосходящей по модулю 25 мм. -
Рост взрослых мужчин является случайной величиной
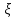 ,
распределенной по нормальному закону:
,
распределенной по нормальному закону:
 .
Найти: плотность вероятности, функцию
распределения этой случайной величины;
вероятность того, что ни один из 3 наудачу
выбранных мужчин не будет иметь рост
менее 180 см.
.
Найти: плотность вероятности, функцию
распределения этой случайной величины;
вероятность того, что ни один из 3 наудачу
выбранных мужчин не будет иметь рост
менее 180 см.
