
КУРСОВАЯ РАБОТА ПО ЛИНЕЙНОЙ АЛГЕБРЕ
.docКУРСОВАЯ РАБОТА ПО ЛИНЕЙНОЙ АЛГЕБРЕ (1 КУРС, 1 СЕМЕСТР)
ВАРИАНТ 19
1. Решить системы: (а)
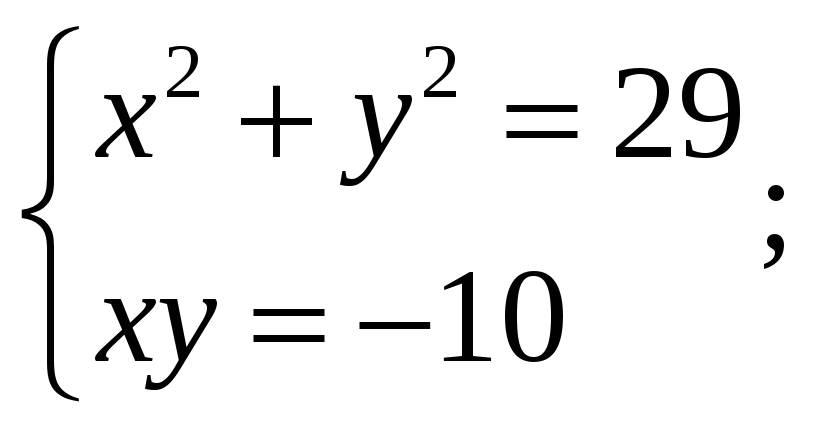 (b)
(b)
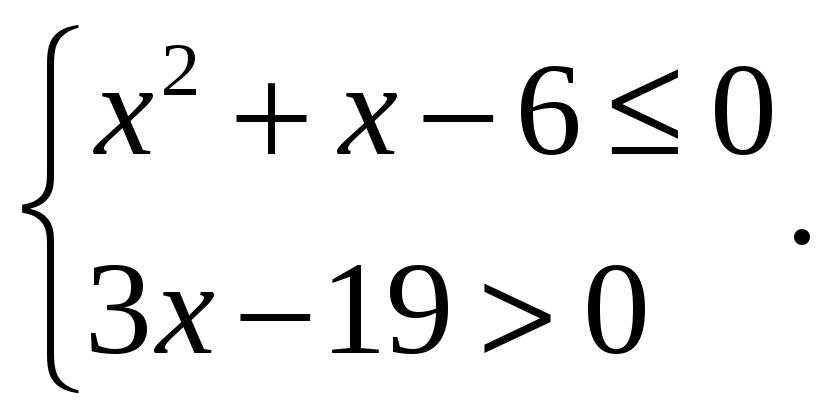
2. Решить уравнения: (a)
![]() (b)
(b)
![]() (c)
(c)![]() (d)
(d)
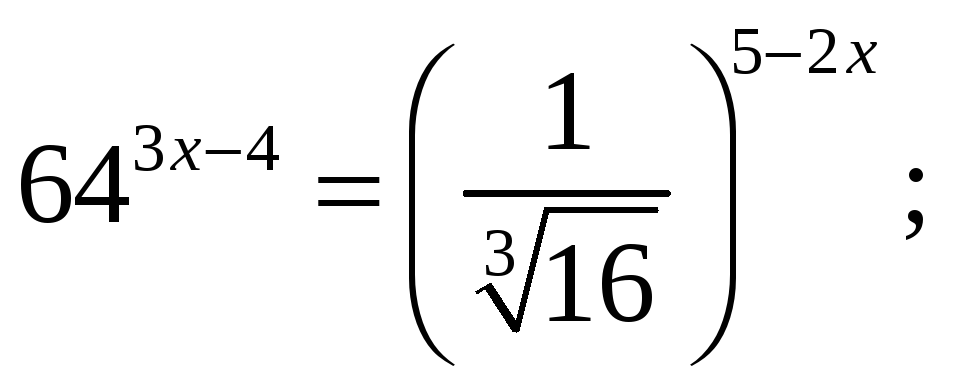 (e)
(e)
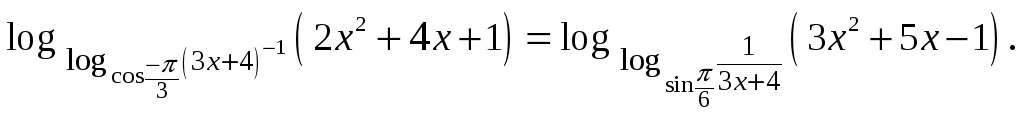
3. Решить неравенства: (a)
![]() (b)
(b)
![]() (c)
(c)
![]()
(d)
![]() (e)
(e)
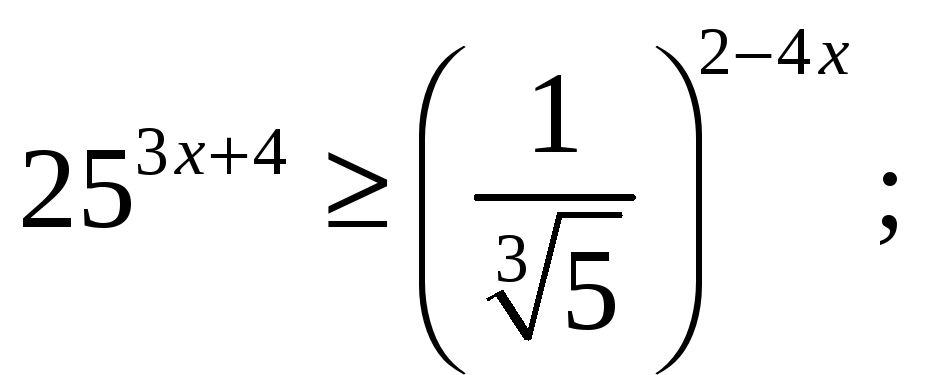 (f)
(f)
![]()
4. Найти область определения функции:
![]()
5. Даны векторы
![]() .
.
Найти: (a)
![]() ;
(b)
;
(b)
![]() ;
(c)
;
(c)
![]() ;
(d)
;
(d)
![]() .
.
6. Даны координаты вершин пирамиды
![]() :
:![]()
![]() .
Найти:
.
Найти:
-
угол между ребрами
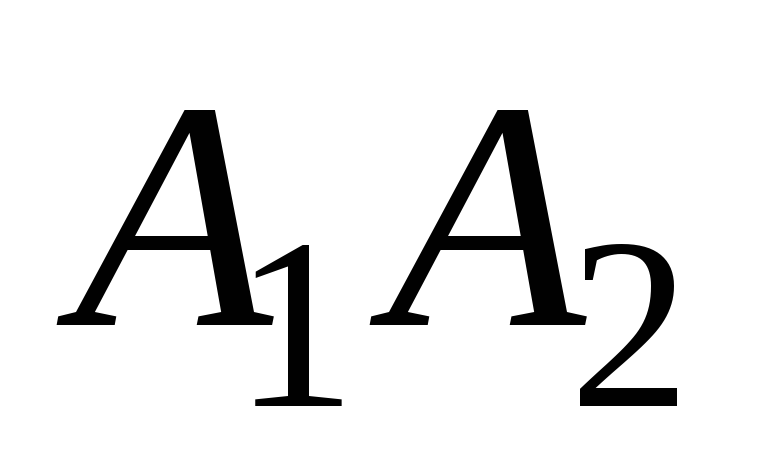 и
и
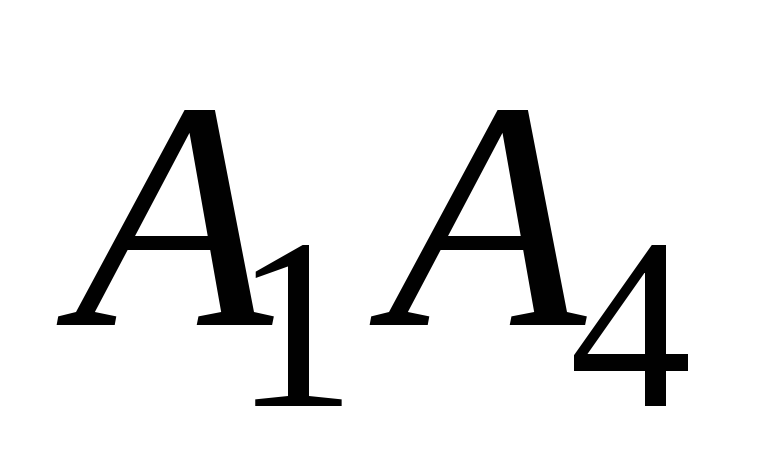 ;
; -
площадь грани
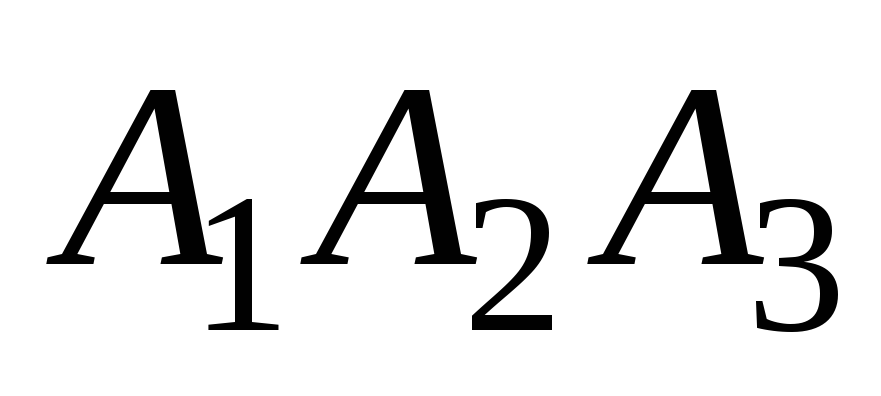 ;
; -
объем пирамиды
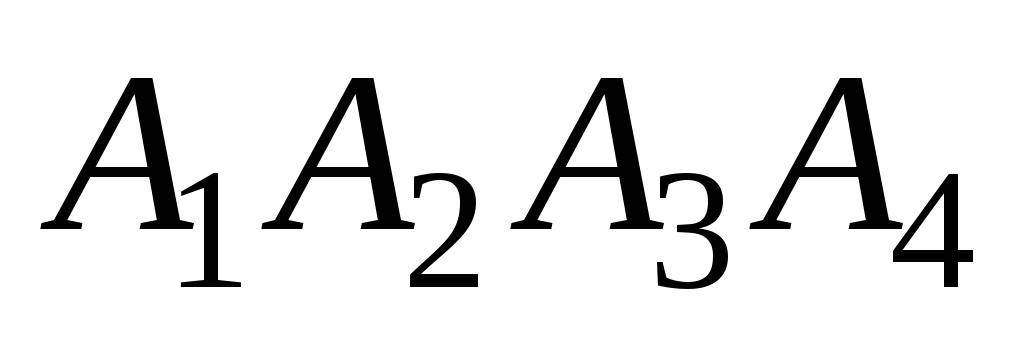 ;
; -
длину высоты
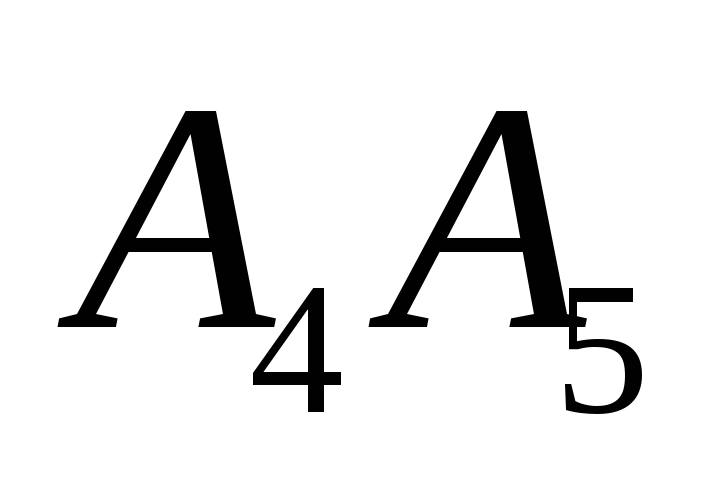 опущенную на грань
опущенную на грань
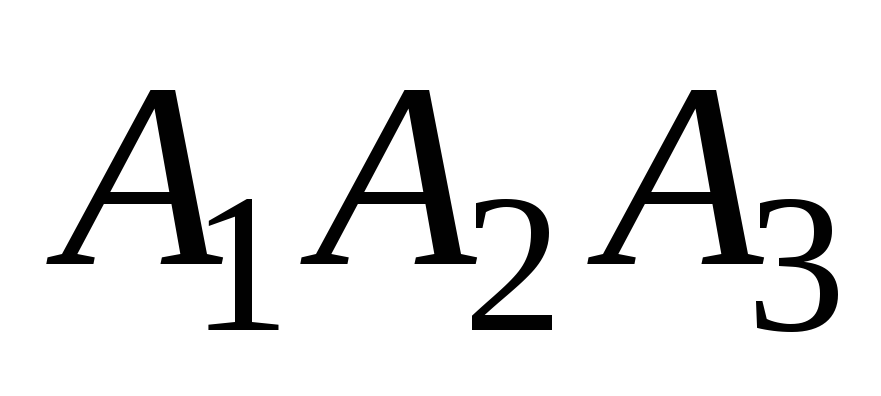 .
.
7. Даны координаты вершины треугольника
![]() :
:
![]() .
.
-
Составить уравнения высоты, биссектрисы и медианы, опущенных из вершины B на сторону AC.
-
Составить уравнение прямой, проходящей через точку C параллельно/перпендикулярно стороне AB.
8. Определить тип кривой, приведя данное уравнение к каноническому виду, и построить ее
-
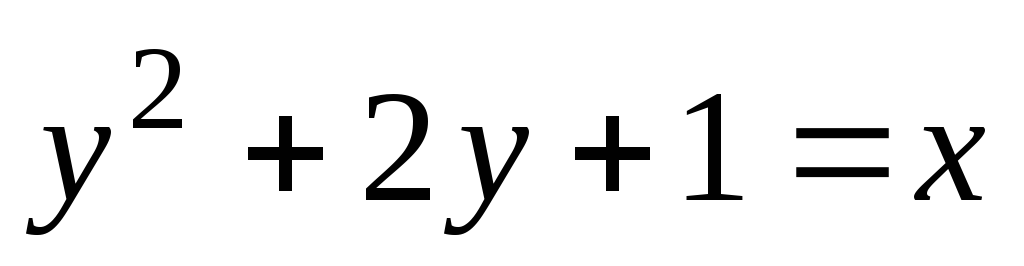 ;
; -
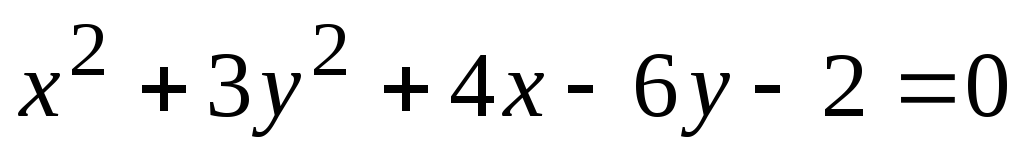 .
.
9. Составить уравнение множества точек,
сумма расстояний которых до двух заданных
![]() и
и
![]() есть величина постоянная, равная 4.
Сделать чертеж.
есть величина постоянная, равная 4.
Сделать чертеж.
10. Даны комплексные числа
![]() .
Найти
.
Найти
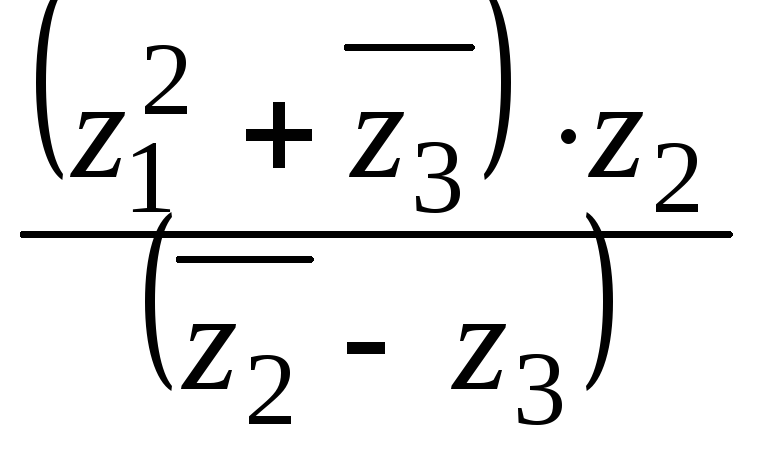 .
.
11. Дано комплексное число
![]() .
.
-
Записать число
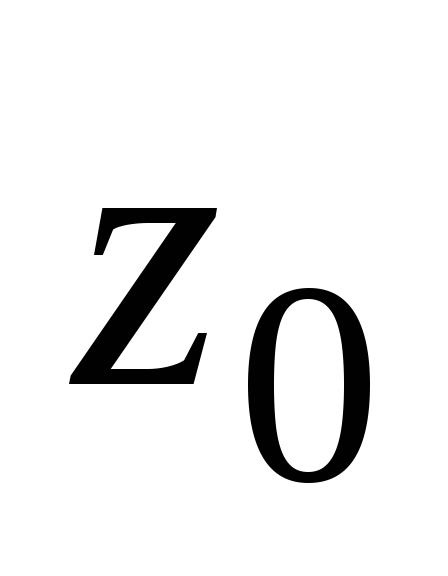 в алгебраической, тригонометрической,
показательных формах;
в алгебраической, тригонометрической,
показательных формах; -
Решить уравнение
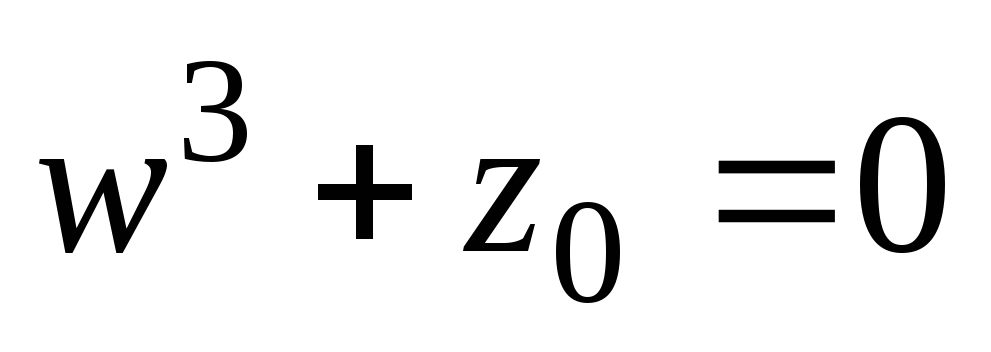 .
.
12. Разложить данные дроби на сумму простейших
(a)
![]() ,
(b)
,
(b)
![]() .
.
13. Вычислить определители матриц
(a)
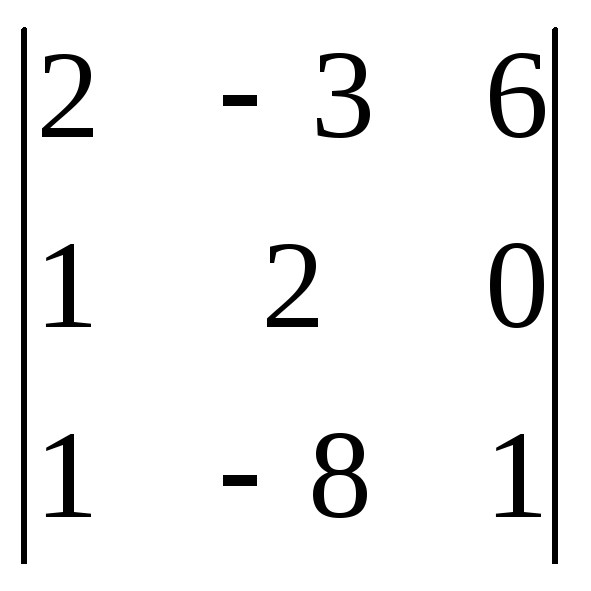 ,
(b)
,
(b)
 .
.
14. Исследовать на совместность и решить системы уравнений:
-
методом Гаусса
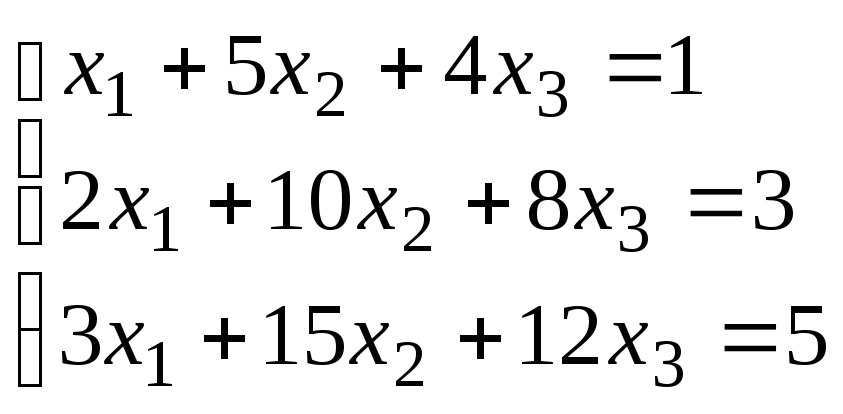 ;
; -
методом Гаусса
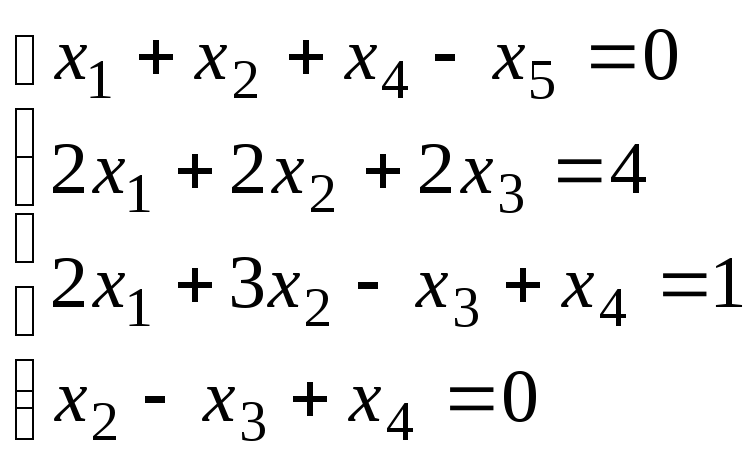 ;
; -
методом Крамера и с помощью обратной матрицы
 .
.
15. Даны матрицы
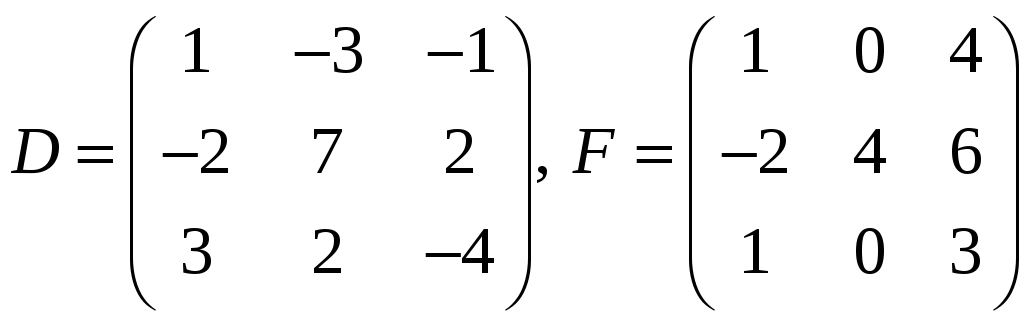 .
.
Решить уравнение
![]() средствами матричного исчисления, при
этом правильность вычисления обратной
матрицы проверить, используя матричное
умножение.
средствами матричного исчисления, при
этом правильность вычисления обратной
матрицы проверить, используя матричное
умножение.
16. Найти собственные значения, собственные и присоединенные векторы матриц:
(a)
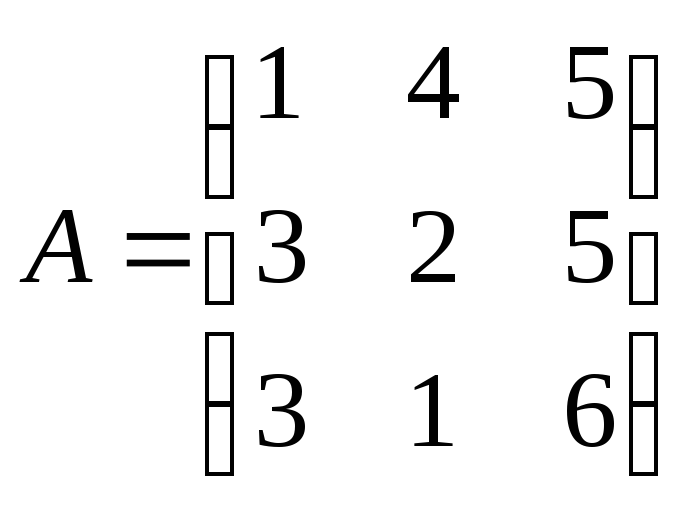 ,
(b)
,
(b)
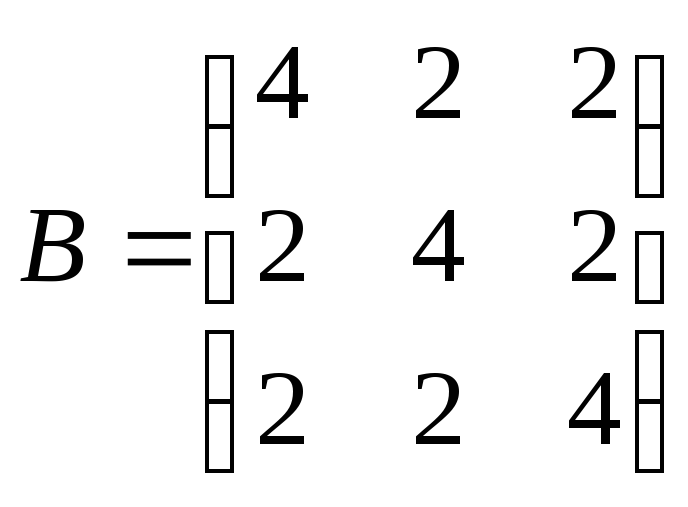 .
.
