
Антенно-фидерные устройства АФУ / практические занятия по курсу антенно-фидерные
.pdf
éS1,1 |
S1,2 |
K S1,m |
|
|
|
S1,m+1 |
KS1,N |
ù |
|
|||||||||
|
|
|||||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
êS |
2,1 |
S2,2 |
K S2,m |
|
|
S2,m+1 |
KS2,N |
ú |
|
|||||||||
|
|
|||||||||||||||||
ê |
|
|
|
M |
|
|
|
|
|
|
|
|
|
M |
|
|
ú |
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
||
ê |
|
S |
|
K S |
|
|
|
|
S |
|
KS |
|
ú |
|
||||
êS |
|
|
|
|
|
|
|
|
ú |
|
||||||||
[S]= ê |
m,1 |
|
|
m,2 |
|
|
m,m |
|
|
|
|
m,m+1 |
|
|
m,N |
ú |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ê- - - - - - - - - - - - - - - - - - - - - - - |
ú |
|
||||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
êSm+1,1 |
Sm+1,2 KSm+1,m |
|
|
Sm+1,m+1 KSm+1,N ú |
|
|||||||||||||
ê |
|
|
|
M |
|
|
|
|
|
|
|
|
|
M |
|
|
ú |
|
ê |
|
S |
|
|
KS |
|
|
|
|
|
S |
|
KS |
|
|
ú |
|
|
êS |
|
|
|
|
|
|
|
|
N ,m+1 |
|
|
ú |
|
|||||
ë |
N ,1 |
|
N ,2 |
|
N ,m |
|
|
|
|
|
|
N ,N |
û |
|
||||
|
|
|
|
|
= é [S1 |
] [S2 |
]ù. |
|
|
|
|
|
||||||
|
|
|
|
|
ëê [S3 |
] [S4 |
]ûú |
|
|
|
|
|
||||||
Тогда окончательная матрица образованного 2N-полюсника будет определяться из выра-
жения
[Sˆ]= [S1 ]- [S2 ]× ([S4 ]- [K ])−1 × [S3 ],
где матрица [K] определяется межсоединениями внутри 2N-полюсника, она имеет ту же размерность, что и матрица [S4 ], лучше всего ее определить из конкретного примера.
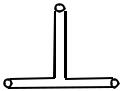
Рассмотрим двухрезонаторный шлейфный фильтр (рис.2).
l l
l 1
Рис.2. Двухрезонаторный шлейфный фильтр
Нумерацию клемм элементарных многополюсников проведем согласно алгоритму, как показано на рис.3.
5 |
6 |
1 |
3 |
4 |
2 |
Рис.3. Разбиение схемы фильтра на элементарные многополюсники
и нумерация клемм согласно алгоритму
PDF created with pdfFactory Pro trial version www.pdffactory.com
Матрица [S] имеет в этом случае вид
|
|
éS |
0 |
|
|
|
|
|
|
S |
|
|
|
0 |
|
|
|
|
|
S |
|
0 |
ù |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
ê |
11 |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ê |
0 S22 |
|
|
|
|
|
|
0 S24 |
0 S26 ú |
|
||||||||||||||||||
|
|
ê- - - - - |
|
- - - - - - - -ú |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
ê |
|
0 |
|
|
|
|
|
|
S33 |
|
|
|
0 S35 |
|
0 |
ú |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
[S]= êS31 |
|
|
|
|
|
|
|
|
|
|
ú, |
|
||||||||||||||||||
|
|
ê |
0 |
S |
42 |
|
|
|
|
|
|
0 |
|
|
S |
44 |
|
|
|
|
|
0 S |
46 |
ú |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
êS51 |
0 |
|
|
|
|
|
|
S53 |
|
|
|
0 S55 |
|
0 ú |
|
|||||||||||||
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
ë |
0 S62 |
|
|
|
|
|
|
0 S64 |
0 S66 û |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[S ]= |
éS11 |
0 ù, [S |
2 |
]= |
éS13 |
|
0 |
|
|
S15 |
|
|
0 ù, |
|
||||||||||||||||
1 |
ê |
|
|
|
ú |
|
|
|
|
|
|
ê |
0 S24 |
|
|
|
|
ú |
|
|||||||||||
|
ë |
0 S22 û |
|
|
|
|
|
|
|
ë |
0 S26 û |
|
||||||||||||||||||
|
éS |
|
0 ù |
|
|
|
|
|
|
|
éS |
|
|
|
0 |
|
S |
|
|
|
0 ù |
|
||||||||
[S3 ]= |
ê |
13 |
|
ú |
|
[S4 |
|
ê |
|
33 |
|
|
|
|
|
|
|
|
|
35 |
|
|
ú |
|
||||||
ê |
0 |
|
S42 ú, |
|
]= |
ê |
0 |
|
|
|
S44 |
0 |
|
S46 ú |
, |
|||||||||||||||
|
êS51 |
0 |
ú |
|
|
|
|
|
|
|
êS53 |
|
|
0 S55 |
|
|
0 ú |
|
||||||||||||
|
ê |
|
|
|
ú |
|
|
|
|
|
|
|
ê |
0 S64 |
|
|
|
|
ú |
|
||||||||||
|
ë |
0 S62 û |
|
|
|
|
|
|
|
ë |
0 S66 û |
|
||||||||||||||||||
матрица [K] - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
5 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
0 |
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
[K ]= 54 |
|
|
|
1 |
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Порядок заполнения матрицы [K]:
1)там, где есть соединение (в нашем случае клемм 3 и 4), ставится единица;
2)там, где стоит нагрузка, ставится диагональный элемент 1 Γi , здесь i - номер клем-
Γi , здесь i - номер клем-
мы.
Пример. Определить матрицу рассеяния шестиполюсника, показанного на рис.4.
|
3 |
|
ρ3, l 3 |
ρ1, l 1 |
ρ1, l 2 |
1 2
Рис.4. Шестиполюсник
PDF created with pdfFactory Pro trial version www.pdffactory.com

Решение. Воспользуемся рекуррентными формулами для определения [S] - матрицы про- извольного 2N-полюсника:
K1 = |
|
|
|
1 |
|
; |
||
1 r1 +1 r2 +K+1 rN |
||||||||
|
|
æ |
2K |
ö |
−2 jθi |
|
|
|
|
|
ç |
÷ |
|
|
|||
Sii |
= |
ç |
|
-1÷e |
|
; |
|
|
ri |
|
|
||||||
|
|
è |
ø |
|
|
|
||
Si, p |
= |
|
|
|
|
2K |
|
|
|
exp(- j(qi |
|
+ qp )); qi |
= |
2p´li |
, j = |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
-1 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ri ´rp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|||||||
(при N = 3 и ρ1 = ρ2 = ρ3 = ρ имеем K1 = ρ 3 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В нашем случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K = |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
|
r1r3 |
|
|
|
; l = l |
|
|
= 0; |
|
|
|
|
|
|
||||||||||||
|
1 r +1 r |
|
+1 r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
2 |
3 |
|
|
2r |
3 |
+ r |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
S = - |
|
|
r1 |
|
; |
|
S |
22 |
= S ; |
|
S |
33 |
= r1 - 2r3 e−2 jθ3 ; |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
11 |
|
|
|
|
|
2r3 |
+ r1 |
|
|
|
|
|
|
11 |
|
|
|
|
2r3 + r1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
S = S |
21 |
= |
|
2r3 |
|
; S = S |
31 |
= |
2 |
r1r3 |
|
e− jθ3 ; |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
12 |
|
|
|
|
|
2r3 + r1 |
|
|
13 |
|
|
|
|
|
2r3 + r1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
S23 = S32 = S13 = S31. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
- r1 |
|
|
|
|
|
|
2r3 |
|
|
|
|
2 |
|
|
e− jθ3 |
ù |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1r3 |
|||||||||||||||||||||||
[S]= |
|
1 |
|
|
|
|
|
ê |
|
|
|
2r |
|
|
|
|
|
|
|
|
|
- r |
|
|
|
2 |
|
e− jθ3 |
ú . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r r |
|||||||||||||||||||||||
|
|
|
|
|
|
|
ê |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
3 |
|
|
|
|
ú |
||||||
|
2r3 + r1 ê2 |
|
|
|
e− jθ3 |
|
2 |
|
|
|
e− jθ3 |
|
(r - 2r |
|
)e−2 jθ3 |
ú |
||||||||||||||||||||||||||||
|
r r |
3 |
|
r r |
3 |
|
|
3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ë |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
û |
|||||||||
Задание. Определить матрицу рассеяния одношлейфного фильтра, показанного на рис.5,а. (Указание: пусть ρ1 = ρ2 = ρ; ρ3 = ρ1, при этом
 Г = 1
Г = 1  3
3
ρ3, l3
ρρ
1 |
2 |
1 |
2 |
а |
|
|
б |
Рис.5. Одношлейфный фильтр: топология (а); представление согласно алгоритму (б)
PDF created with pdfFactory Pro trial version www.pdffactory.com
допустим, что l1 = l2 = 0 , тогда фильтр может быть представлен в виде, показанном на рис.5,б. Далее расчет проводить в соответствии с алгоритмом.)
Литература
1. Силаев Г.М., Брянцев И.С. Применение матрицы и графов к анализу СВЧ- устройств. - М.: Сов. радио, 1973. - С. 5 - 56.
PDF created with pdfFactory Pro trial version www.pdffactory.com
Семинар № 4. Проектирование делителей мощности
Определение геометрических параметров делителей мощности в виде кольцевого и двухшлейфного НО с коэффициентом деления m
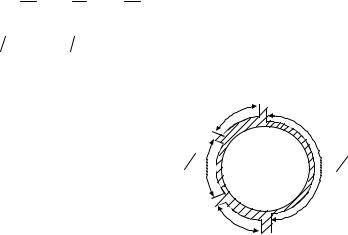
Кольцевой НО показан на рис.1. Общая длина кольца равна 3Λ 2 , длины отрезков ли-
2 , длины отрезков ли-
нии передачи между различными выходами и их волновые сопротивления по входам та-
кого НО будут определяться как
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
+ y2 |
- y2 |
= 0 или Y 2 |
+Y 2 =1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
0 |
|
1 |
2 |
где |
y |
|
= |
1 |
, y = |
1 |
, y |
|
= |
1 |
- проводимости соответствующих отрезков линии передачи; |
||||||||
|
|
0 |
|
r |
0 |
1 |
r |
|
|
2 |
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
Y1 = y1 |
|
y0 ,Y2 = y2 |
y0 |
- так называемые нормированные проводимости. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ρ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Λ 4 |
ρ1 |
|
ρ1 |
3Λ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ0 |
|
ρ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ0 |
4 |
|
Рис.1. Топология кольцевого НО длиной 3Λ/2
Матрица рассеяния кольцевого НО имеет следующий вид:
é 0
[ ] êY
S = - jê 1 êêY2
ë 0
Y1 |
Y2 |
0 |
ù |
0 |
0 |
Y |
ú |
|
|
2 |
ú |
0 |
0 |
-Y1 |
ú |
ú |
|||
Y2 |
-Y1 |
0 |
û |
Принцип работы такого НО легко просматривается из условия сложения сигналов в выходных плечах при возбуждении любого из четырех входов. Как видно из матрицы рас- сеяния, при возбуждении любого входа сигнал поступает только на смежные с ним выхо- ды, а противоположное плечо всегда остается развязанным. Таким образом, представлен- ный тип НО - противонаправленный.
PDF created with pdfFactory Pro trial version www.pdffactory.com
Если нагрузить развязанный выход на согласованную нагрузку, то легко реализуется де- литель мощности. В случае возбуждения входа 1 мощность поступает на выходы 2 и 3, при- чем коэффициент деления мощности связан с параметрами кольцевого НО следующим соот- ношением:
m = |
P |
= |
|
S12 |
|
|
2 |
= |
Y 2 |
(1) |
||
|
|
|
||||||||||
2 |
|
|
|
|
|
|
1 |
. |
||||
|
|
|
|
|
|
|
|
|||||
|
P3 |
|
|
S |
|
|
2 |
|
Y22 |
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
13 |
|
|
|
|
|
|
|
|
С учетом условия идеального согласования (1) имеем
Y = |
|
m |
|
и |
Y = |
|
1 |
|
, |
(2) |
|
|
|||||||||
1 |
|
m +1 |
|
2 |
|
m +1 |
|
|
||
|
|
|
|
|
|
|
||||
тогда матрица рассеяния кольцевого делителя мощности может быть записана в виде
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ù |
|
|
|
|
0 |
|
- j |
|
m |
- |
j |
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
||||||||||
|
m +1 |
|
m +1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|||||
ê |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ú |
|
|
|
|
|||||
ê- j |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
- j |
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
||||
|
m +1 |
|
|
|
|
|
|
m +1 |
|
|
|
|
|||||||||||||||||||
[S]= ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú . |
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|||||
ê- j |
|
|
0 |
|
|
0 |
|
|
|
|
j |
|
|
|
|
ú |
|
|
|
|
|||||||||||
|
m +1 |
|
|
|
|
|
m +1 |
|
|
|
|
||||||||||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ê |
0 |
|
- j |
j |
|
|
|
|
|
|
0 |
|
|
|
|
ú |
|
|
|
|
|||||||||||
ê |
|
|
m +1 |
|
m +1 |
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|||||||||||||
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
||||||
Так, для частного случая m = 1 (гибридное кольцо) имеем |
|
S |
|
|
= |
|
S |
|
|
или Y = Y |
= 1 |
2 |
. |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
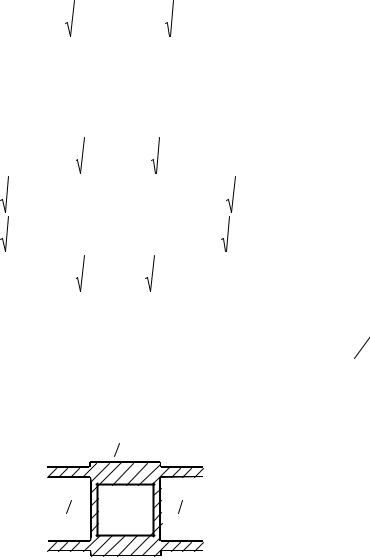
Длины отрезков линии передачи двухшлейфного НО и их волновые сопротивления показаны на рис.2.
ρ0 |
Λ 4 |
|
ρ0 |
1 |
ρ2 |
|
3 |
Λ 4 |
|
Λ 4 |
|
ρ1 |
ρ1 |
||
ρ0 |
ρ2 |
|
ρ0 |
2 |
|
|
4 |
Λ 4
4
Рис.2. Топология двухшлейфного НО
Условие идеального согласования для такого НО запишется в виде
Y12 = Y22 -1,
PDF created with pdfFactory Pro trial version www.pdffactory.com

где Y1 и Y1 - нормированные проводимости соответствующих отрезков линии передач
(Y1 = r0 , Y2 = r0 ). r1 r2
Матрица рассеяния двухшлейфного НО имеет следующий вид:
|
|
|
é 0 |
0 |
j |
Y |
ù |
|
|
|
1 |
ê |
0 |
Y1 |
1 |
ú |
|
[S]= - |
|
ê 0 |
j |
ú |
(3) |
|||
|
|
|
0 |
0 |
||||
|
1+ Y 2 |
ê j Y1 |
ú |
|
||||
1 |
ê |
j |
0 |
0 |
ú |
|
||
|
|
|
ëY1 |
û |
|
|||
Матрица рассеяния (3) позволяет сделать вывод о том, что данный НО является сона-
правленным и сигналы в выходных плечах сдвинуты по фазе относительно друг друга на постоянную величину, равную π 2 . Это является отличительной особенностью двух-
2 . Это является отличительной особенностью двух-
шлейфного НО.
Если нагрузить развязанный выход этого НО на согласованную нагрузку, то, как и в предыдущем случае, легко реализуется на его основе делитель мощности. В случае воз- буждения входа 1 (см. рис.2) мощность поступает на выходы 3 и 4, причем коэффициент деления мощности связан с параметрами двухшлейфного НО следующим соотношением:
m = |
P |
= |
|
S13 |
|
|
2 |
= |
1 |
= |
1 |
|
||
|
|
|
|
|||||||||||
3 |
|
|
|
|
|
|
|
|
|
. |
||||
P4 |
|
S |
|
|
2 |
Y12 |
Y22 |
-1 |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
Отсюда
Y12 = m1 и Y22 = mm+1 ,
матрица рассеяния имеет следующий вид:
|
|
|
é |
0 |
|
0 |
|
|
|
j |
1 |
ù |
|||||
|
|
|
ê |
|
|
|
|
|
|
|
ú |
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
ê |
|
|
|
|
|
|
|
1 |
|
|
m ú |
|||
|
|
|
ê |
0 |
|
0 |
|
|
|
|
j |
ú |
|||||
|
|
m |
|
|
|
|
|
|
|
||||||||
[S]= - |
ê |
|
|
|
|
|
|
|
|
m |
|
|
ú |
||||
|
ê |
|
|
|
1 |
|
|
|
|
|
|
|
ú . |
||||
m +1 |
|
j |
0 |
|
0 |
||||||||||||
|
|
ê |
|
|
|
|
|
|
ú |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
m |
|
||||||||||||
|
|
|
ê |
1 |
|
|
|
|
|
|
|
ú |
|||||
|
|
|
ê |
|
|
j |
0 |
|
0 |
ú |
|||||||
|
|
|
ê |
|
|
|
|
|
ú |
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
m |
|
|
|||||||||||
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
û |
|||
PDF created with pdfFactory Pro trial version www.pdffactory.com

В |
частном |
случае |
гибридного |
двухшлейфного |
мостового |
НО |
(m = 1) имеем
S13 |
|
= |
|
S14 |
|
или Y1 =1, Y2 = |
|
|
|
|
|
2. |
|||||
Проектирование развязанного кольцевого делителя мощности
Равномерное деление мощности. Наиболее широкое распространение в СВЧ- технике получил развязанный кольцевой делитель мощности (рис.3). Его основные досто- инства по сравнению с вышеприведенными делителями мощности - малые габариты, про- стота изготовления, меньшее количество входов. Он не требует применения согласован- ной нагрузки. В СВЧ-технике по отношению к нему применяется термин “бинарный делитель мощности”. Существенным его недостатком является то, что он делит мощность, поступающую на вход 1, только пополам.
|
|
Λ 4 |
|
2 |
B |
ρ1 |
|
ρ0 |
|
||
|
|
||
|
R |
A |
|
|
1 |
||
ρ0 |
C |
ρ0 |
|
ρ1 |
|||
3 |
|
||
|
|
Λ 4
4
Рис.3. Топология развязанного кольцевого делителя мощности
Принцип действия этого делителя заключается в следующем. Если возбуждается вход 1 (см. рис.3), то в силу симметрии сигнал поровну делится между плечами 2 и 3, при этом точки В и С эквипотенциальны и через сопротивление R ток не идет.
Пусть теперь сигнал поступает в плечо 2, тогда в точку С он попадает через сопротив- ление R и через два четвертьволновых отрезка ВА и АС, т.е. в противофазе. При опреде-
ленном выборе R и ρ1 относительно ρ0 можно обеспечить равенство по амплитуде двух указанных сигналов и, следовательно, полную компенсацию энергии в точке С. Таким об- разом, плечи 2 и 3 будут развязаны. При этом половина мощности поступает в плечо 1, а половина рассеивается на сопротивлении R.
Выбор значений R и ρ производится из известных коэффициентов матрицы рассеяния данного шестиполюсника. Воспользуемся только четырьмя коэффициентами:
PDF created with pdfFactory Pro trial version www.pdffactory.com
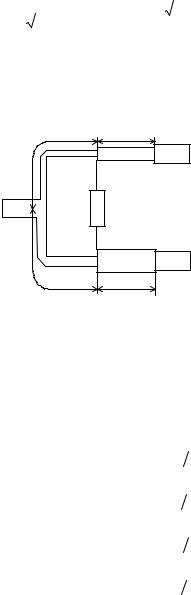
|
1- 2Y 2 |
|
1 |
æ |
1- 2Y 2 |
|
1-Y |
ö |
||
S11 = |
1 |
; S22 |
= S33 = 2 |
ç |
1 |
+ |
|
2 |
÷ |
|
1+Y |
||||||||||
1+ 2Y 2 |
ç |
1+ 2Y 2 |
÷; |
|||||||
|
1 |
|
|
è |
1 |
|
2 |
ø |
||
1 |
æ |
1- 2Y 2 |
|
1-Y |
ö |
|
||
S23 = 2 |
ç |
1 |
- |
|
2 |
÷ |
, |
|
1+Y |
||||||||
ç |
1+ 2Y 2 |
÷ |
||||||
|
è |
1 |
|
2 |
ø |
|
||
где Y1 = ρ0 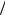 ρ1 и Y2 = 2ρ0
ρ1 и Y2 = 2ρ0 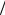 ρ1 .
ρ1 .
Идеальное согласование трех плеч делителя (S11 = S22 = S33 ) и идеальная развязка плеч
делителя 2 и 3 (S23 = 0) получаются при следующих значениях: |
|
|
||||||||
Y = |
1 |
|
,Y =1 |
или r = r |
|
|
и R = 2ρ |
|
. |
|
|
0 |
2 |
0 |
|||||||
|
|
|
||||||||
1 |
2 |
2 |
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
||
Неравномерное деление мощности. Схема кольцевого делителя мощности с развя- занными выходами, способного обеспечить неравномерное деление мощности, показана на рис.4.
θ2 |
θ4 |
2 |
|
|
|
ρ2 |
|
ρ0 |
ρ4 |
|
|
|
|
|
1 |
|
|
ρ0 |
R |
|
ρ3 |
ρ5 |
3 |
|
||
|
|
ρ0 |
θ3 |
θ5 |
|
Рис.4. Топология кольцевого делителя мощности с неравномерным делением
мощности
Электрические длины линий передач делителя равны
q2 |
= |
|
2p´l2 |
, l2 = L2 4; |
|||||
|
|
|
|||||||
|
|
|
|
L2 |
|
|
|||
q |
3 |
= |
|
2p´l3 |
|
, l = L |
3 |
4; |
|
|
|
||||||||
|
|
|
3 |
|
|||||
|
|
|
|
L3 |
|
|
|||
q4 |
= |
|
2p´l4 |
, l4 = L4 4; |
|||||
|
|
|
|||||||
|
|
|
|
L4 |
|
|
|||
q |
5 |
= |
|
2p´l5 |
, l = L |
5 |
4. |
||
|
|
||||||||
|
|
|
5 |
|
|||||
|
|
|
|
L5 |
|
|
|||
Еcли задать коэффициент деления по напряжению Ku = U2/U3, то волновые сопротив-
ления отрезков линий передачи делителя можно записать в виде
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
|
|
; ρ3 = ρ0 |
|
; ρ4 = ρ0 |
|
; |
|
|
Ku (1+ Ku )2 |
||||||||
ρ2 = ρ0 |
(1+ Ku2 ) Ku |
||||||||
Ku |
|||||||||
ρ5 = ρ0 |
|
|
, |
||||||
|
Ku |
||||||||
а сопротивление - как R = ρ0 (1+ Ku2 ) Ku .
Ku .
Пример. Определить геометрические параметры делителя в виде кольцевого НО с ко- эффициентом деления мощности m = 4 на МПЛ с поликоровой подложкой толщиной h = 1
мм, ε = 9,8; частота f = 5 ГГц; входное сопротивление ρ0 = 50 Ом.
Решение. 1. Из соотношений (1) и (2) определим значения нормированных проводи- мостей Y1 и Y2 (см. рис.1):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y = |
4 |
≈ 0,894; |
Y = |
1 ≈ 0,447, |
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
5 |
|
|
|
2 |
5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отсюда.ρ = ρ0 |
≈ 56 Ом; ρ |
2 |
= ρ0 |
≈112 Ом. |
|
|
|
|
|
|
|
|
|
|||||||
1 |
Y1 |
|
|
Y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Воспользуемся графиками зависимости W от ρ и |
|
от h, откуда определим |
||||||||||||||||||
εэф |
||||||||||||||||||||
|
|
|
|
W0 ≈ 0,98 мм; |
W1 ≈ 0,7 мм; |
W2 ≈ 0,09 мм; |
||||||||||||||
|
|
|
|
|
|
|
|
|
= 2,54; |
|
|
= 2,53; |
|
|
|
|
= 2,48. |
|||
|
|
|
|
|
εэф |
0 |
|
|
εэф |
|
εэф |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
3. Используя зависимость Λ = λ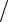

 εэф , определим соответствующие длины волн в ли-
εэф , определим соответствующие длины волн в ли-
ниях передачи:
Λ0 ≈ 2,36 см; Λ1 ≈ 2,37 см; Λ2 ≈ 2,42 см.
4. Определим длину отрезков линий кольца:
l1 = Λ1  4 = 5,9 мм; l2 = Λ2
4 = 5,9 мм; l2 = Λ2  4 = 5,9 мм; l3 = 3Λ1
4 = 5,9 мм; l3 = 3Λ1  4 = 17,7мм.
4 = 17,7мм.
5. Рассчитаем средний, внутренний и наружный диаметры кольца:
d |
ср |
= |
l1 + 2l2 + l3 |
=11,26 мм; |
d |
вм |
= d |
ср |
−W =10,56 мм; |
|
|||||||||
|
|
π |
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
dн = dср +W1 =11,96 мм.
PDF created with pdfFactory Pro trial version www.pdffactory.com
