шпоры металлы / 8

8. Работа и расчет изгибаемых э-тов в упругопластической стадии. Подбор сечений. Работа и расчет изгибаемых элементов с учетом развития пласти­ческих дефор-маций.

После исчерпания упругой работы (рис. 3.12а), в сплошных изгибаемых элементах, выполненных из пластичных сталей, пластические деформации начинают распространяться в глубь сечения (рис. 3.12б), и в предельном состоянии они пронизывают все сечение (рис. 3.12в), образуя так называемый «шарнир пластичности».

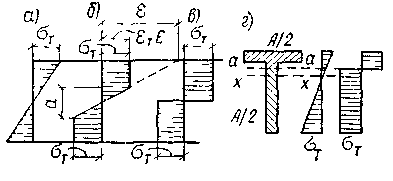
Рис. 3.12.Последовательное изменение эпюры напряжений при изгибе

а — упругое состояние; б — упругопластическое состояние при наличии упругого ядра; в — шар­нир пластичности; г — упругая работа и шарнир пластичности несимметричного сечения.

При образовании шарнира пластичности все фибры сечения нахо­дятся в стадии текучести и, следовательно, их длина может изменяться при постоянном напряжении, вследствие чего изгибаемый элемент мо­жет поворачиваться вокруг нейтральной оси, как вокруг оси шарнира. Работа шарнира пластичности возможна только в направлении дейст­вия предельного момента; при действии изгибающего момента в обрат­ном направлении напряжения уменьшаются, материал снова становится упругим и шарнир пластичности замыкается. В отличие от обычного шарнира в пластическом шарнире момент не равен нулю.

Предполагая сталь идеально упругопластическим материалом и допуская, что напряжения во всех фибрах достигнут пре­дела текучести, можно определить предельное значение момента шар­нира пластичности. Эпюра напряжений такого состояния имеет вид двух прямоугольников с ординатами, равными пределу текучести. Предельный момент внутренних сил определяется из вы­ражения

где S — статический момент половины сечения относительно нейтральной оси. Для сим­метричных сечений нейтральная ось проходит через центр тяжести сечения, в несим­метричных сечениях нейтральная ось делит сечение на две равновеликие части и не совпадает с центром тяжести. Сравнивая формулу (3.21) с обычной формулой M = σ_TW, где М — предельный момент, определенный по упругой стадии работы материа­ла, видим, что 2S играет роль пластического момента сопротивления; W^пл = 2S. Пластический момент сопротивления W^пл больше упругого момента сопротивления W, и разница тем боль-ше, чем больше материала расположе-но около нейтральной оси сечения. Для прямоугольного сечения W^пл =1,5W, для прокатных швеллеров и двутавров при изгибе в плос­кости стенки W^пл = 1,2W, при изгибе в плоскости, параллельной пол­кам, W^пл =1,2 W. Фактическая диаграмма работы материала отличается от идеализи­рованной диаграммы Прандтля, однако эти отличия несущественно ска­зываются на величине предельного пластического момента (не более 1—2 %) и идут в запас прочности. Совместное воздействие нормальных и касательных напряжений ускоряет развитие пластичности, и предельный момент М_пр^Q при нали­чии поперечной силы будет меньше предельного момента М_пр^Q приQ = 0, т. е. т= (М_пр^Q / М_пр⁰) <1. Это же относится и к предельной попереч­ной силе, т.е. n= (Q_пр^M / Q_пр⁰) <1, где Q_пр^M —предельная поперечная сила при одновременном действии момента; Q_пр⁰—предельная поперечная си­ла при М = 0.

Рис. 3.13 Линия перехода материала балки в пластическое состояние.

При совместном действии М и Q условие образования шарнира пла­стичности определяется некоторой функцией Ф величин т и n . Уравнение граничной линии перехода материала в пластическое со­стояние для прямоугольных сечений можно задать в виде окружности т² + n²=1. Для других типов сечения Б. М. Броуде предложил приве­сти его к виду

Ф= т² + n²-amn=1

Для двутавра a≈0,8...0,9.

Точное решение полученного уравнения получается весьма громозд­ким, поэтому для упрощения расчета с до-статочной для практики точ­ностью (с небольшим запасом), согласно СНиП II-23-81, приведенные напряжения проверяют по текучести в точке а, распространение пласти­ческих деформаций по стенке учитывают эквивалентным повышением расчетного сопротивления на 15 %. В общем случае приведенные нап­ряжения в стенке балок при действии нормальных напряжений в двух направлениях σ_х и σ_y и касательных напряженийпроверяют по фор­муле

<³-²³>

При этом каждое из напряжений не должно превышать расчетного сопротивления, т. е.:

σ_x≤R; σ_y≤R;

где σ_х = М_y/I_х — нормальное напряжение, параллельное оси балки; σ_y— напряжения, в местах приложения сосредоточенных нагрузок к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости; τ=QS/It — каса­тельное напряжение; t — толщина стенки; S — статический момент отсеченной части.

Рис. 3.14. Работа изгибаемого элемента под нагрузкой

а—развитие пластических деформаций по длине балки, б— г - напряжения в разных сечениях; д — развитие пластических деформаций в зоне чистого изгиба, е— прогибы балки.

В упругой стадии работы элемента прогибы нарастают пропорцио­нально нагрузке (см. участок о—а рис3.14е), затем при развитии пластических деформаций прогибы быстро растут (участок а—б рис3.14е) и, на­конец, при образовании шарнира пластичности, если не учитывать работу материала в стадии самоупрочнения, прогибы нарастают беспре­дельно (участок б— рис 3.14е).Для разрезных балок дальнейшее увеличение нагрузки невозможно, т. е. наступает предельное состояние первой группы (по несущей спо­собности и непригодности к эксплуатации) вследствие чрезмерного развития пластических деформаций. Для не-разрезных балок образование шарнира пластичности приводит к перераспределению моментов и пони­жению степени статической неопределимости конструкции. Расчет изгибаемых элементов при ограниченном развитии пластичес­ких деформаций. Как уже отмечалось, при образовании шарнира пластичности в се­чении изгибаемого элемента происходят неограниченный рост пласти­ческих деформаций и нарастание прогибов. Эксплуатационные качества конструкции утрачиваются раньше, чем наступает беспредельное нарастание деформаций и исчерпание не­сущей способности, так как остаточные деформации (после снятия на­грузки) получаются столь большими , что конструкция становится непригодной к эксплуатации.

В 1952 г. Н. С. Стрелецкий предложил принимать в качестве крите­рия предельного состояния по непригодности к эксплуатации ограничен­ную пластическую деформацию в сечении. Для практических расчетов принята предельная относительная пластическая деформация в сечении где

Учет пластической работы стали допускается в балках сплошного сечения, несущих статическую нагрузку при касательных напряжениях τ≤R_ср.

Проверка прочности таких балок выполняется по формуле М/с₁W_нт,min≤R_y

где М — изгибающий момент; W_нт,min — момент сопротивления; с₁—коэффициент, учи­тывающий развитие пластических деформаций по сечению. При т≤0,5 R_cp влияние касательных напряжений на развитие пла­стичности несущественно и коэффициент с₁= с. При 0,5 R_cp < τ <0,9 R_cp значения коэффициента с₁ принима-ются по формуле

где α — коэффициент, равный 0,7 для двутавров, изгибаемых в плоскости стенки (для других типов сечения а=0); τ=Q/th — средние касательные напряжения. Коэффициент с зависит от формы сечения и степени развития пла­стических деформаций. При изгибе балки в двух главных плоскостях х и у проверка проч­ности выполняется по формуле

М_х/с_х W_x,нт,_min + M_y/с_у W_y,нт,_min ≤Rγ.

При этом касательные напряже­ния не должны превышать 0,5 R_cv.

Проверка предельного состоя­ния возможна только при распростране­нии пластического течения материа­ла на малой длине изгибаемого эле­мента. При значительной протяжен­ности зоны пластических деформа­ций, например при наличии зоны чи­стого изгиба об­щие прогибы получаются столь зна­чительными, что изгибаемый элемент становится непригодным для эксплуатации раньше, чем пластические деформации в сечении достиг­нут величины .

Поэтому при наличии зоны чистого изгиба вместо коэффициентов с₁,c_х и с_у следует принимать соответст­венно

c_1m = 0,5 (1 + с); с_хт = 0,5 (1+с_х);

с_уn = 0,5 (1 + с_у).