
- •Проектирование антенно-фидерных устройств
- •Методические указания к практическим занятиям по курсу “Антенно-фидерные устройства”
- •Введение
- •Список употребляемых сокращений
- •Семинар № 1. Расчет основных параметров МПЛ
- •Семинар № 2. Определение матриц рассеяния элементарных многополюсников
- •Семинар № 4. Проектирование делителей мощности
- •Семинар № 5. Проектирование коммутаторов и фазовращателей
- •Семинар № 6. Расчет характеристик системы линейных вибраторов и антенн бегущей волны
- •Семинар № 7. Способы возбуждения симметричных вибраторов
- •Семинар № 8. Рупорные антенны
- •Семинар № 9. Расчет линзовых антенн
- •Семинар № 10. Расчет антенн поверхностных волн
- •Семинар № 11. Проектирование линейной ФАР с заданным уровнем боковых лепестков
- •Семинар № 12. Эффективность параболических зеркальных антенн
- •Семинар № 13. Проектирование передающих АФАР
- •Семинар № 14. Проектирование приемных АФАР. Расчет их энергетических параметров
- •Семинар № 15. Влияние амплитудно-фазового разброса на энергетические характеристики АФАР
- •Семинар № 16. Проектирование микрополосковых антенн
- •Семинар № 17. Адаптивные антенные решетки
Семинар № 4. Проектирование делителей мощности
Определение геометрических параметров делителей мощности в виде кольцевого и двухшлейфного НО с коэффициентом деления m
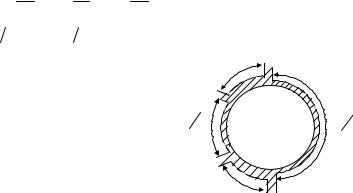
Кольцевой НО показан на рис.1. Общая длина кольца равна 3L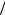 2 , длины отрезков
2 , длины отрезков
линии передачи между различными выходами и их волновые сопротивления по входам такого НО будут определяться как
y12 + y22 - y02 = 0 или Y12 + Y22 = 1,
где y |
0 |
= |
1 , y = |
1 , y |
2 |
= 1 |
- проводимости соответствующих отрезков линии передачи; |
||
|
|
1 |
r1 |
r2 |
|
|
|
||
|
|
|
r0 |
|
|
|
|
||
Y1 = y1 |
y0 ,Y2 = y2 |
y0 - так называемые нормированные проводимости. |
|||||||
|
|
|
|
|
|
|
|
ρ0 |
3 |
|
|
|
|
|
|
|
ρ0 |
|
|
|
|
|
|
|
|
|
1 |
ρ2 |
|
|
|
|
|
|
|
|
Λ 4 |
|
3Λ 4 |
|
|
|
|
|
|
|
ρ1 |
|
ρ1 |
|
|
|
|
|
|
|
ρ0 |
ρ2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
ρ0 |
4 |
Рис.1. Топология кольцевого НО длиной 3Λ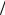 2
2
Матрица рассеяния кольцевого НО имеет следующий вид:
é 0
[ ] êY
S = - jê 1 êêY2 ë 0
Y1 |
Y2 |
0 |
ù |
0 |
0 |
Y |
ú |
|
|
2 |
ú . |
0 |
0 |
-Y1 |
ú |
ú |
|||
Y2 |
-Y1 |
0 |
û |
Принцип работы такого НО легко просматривается из условия сложения сигналов в выходных плечах при возбуждении любого из четырех входов. Как видно из матрицы рассеяния, при возбуждении любого входа сигнал поступает только на смежные с ним выходы, а противоположное плечо всегда остается развязанным. Таким образом, представленный тип НО - противонаправленный.
Если нагрузить развязанный выход на согласованную нагрузку, то легко реализуется делитель мощности. В случае возбуждения входа 1 мощность поступает на выходы 2 и 3,
причем коэффициент деления мощности связан с параметрами кольцевого НО следующим соотношением:
|
P |
|
S12 |
|
|
2 |
|
Y 2 |
|
||
|
|
|
|
|
|
||||||
m = |
2 |
= |
|
|
|
|
|
= |
1 |
. |
(1) |
|
|
|
|
|
|
|
|||||
|
P3 |
|
S |
|
|
2 |
|
Y22 |
|
||
|
|
|
|
|
|
||||||
|
|
|
13 |
|
|
|
|
|
|
|
|
С учетом условия идеального согласования (1) имеем
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
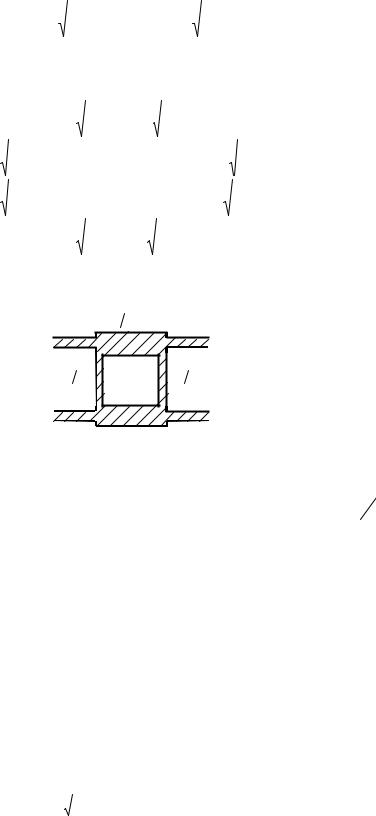
Y = |
|
m |
|
и Y = |
|
1 |
|
, |
(2) |
|
|
||||||||
1 |
|
m +1 |
2 |
|
m +1 |
|
|
||
|
|
|
|
|
|
||||
тогда матрица рассеяния кольцевого делителя мощности может быть записана в виде
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ù |
|
0 |
- j |
|
m |
- j |
|
1 |
|
|
|
0 |
|
||||||
ê |
|
|
|
|
|
|
|
|
|
ú |
|||||||
|
m +1 |
|
m +1 |
|
|
||||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
||||
ê |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ú |
ê- j |
|
|
|
0 |
|
|
|
0 |
|
- |
j |
|
|
|
ú |
||
|
m +1 |
|
|
|
|
|
m +1 |
||||||||||
[S] = ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
ú . |
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||
ê- j |
|
0 |
|
|
|
0 |
|
j |
|
|
ú |
||||||
|
m +1 |
|
|
|
|
|
m +1 |
||||||||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
||||
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
1 |
|
|
|
|
m |
|
|
|
|
|
|
||
ê |
0 |
- j |
|
j |
|
|
|
0 |
|
ú |
|||||||
ê |
|
m +1 |
m +1 |
|
|
|
ú |
||||||||||
ë |
|
|
|
|
|
|
|
|
|
|
|
û |
|||||
ρ0 |
Λ 4 |
|
ρ0 |
1 |
ρ2 |
|
3 |
Λ 4 |
|
Λ 4 |
|
ρ1 |
ρ1 |
||
ρ0 |
ρ2 |
|
ρ0 |
2 |
|
|
4 |
Λ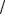 4
4
Рис.2. Топология двух-шлейфного НО
Так, для частного случая m = 1 (гибридное кольцо) имеем |
|
S |
|
= |
|
S |
|
или Y = Y |
= 1 |
|
. |
|
|
|
|
|
|
||||||||
|
|
12 |
|
|
|
13 |
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|||||||
Длины отрезков линии передачи двухшлейфного НО и их волновые сопротивления показаны на рис.2.
Условие идеального согласования для такого НО запишется в виде
|
|
|
|
Y 2 |
= Y 2 |
-1, |
|
|
|
|
1 |
2 |
|
где Y1 и Y2 |
- |
нормированные проводимости соответствующих отрезков ли- |
||||
нии передач (Y = |
r0 |
, Y = |
r0 |
). |
|
|
|
|
|
|
|||
1 |
r1 |
2 |
r2 |
|
|
|
|
|
|
|
|
||
Матрица рассеяния двухшлейфного НО имеет следующий вид:
|
|
|
é 0 |
0 |
j |
Y |
ù |
|
||
|
|
1 |
ê |
0 |
0 |
Y1 |
1 |
ú |
|
|
[S]= - |
|
|
ê |
j |
ú . |
(3) |
||||
|
|
|
|
|
|
|
||||
2 |
ê |
j Y1 |
0 |
0 |
ú |
|
||||
|
1+ Y1 |
ê |
ú |
|
||||||
|
|
|
|
ëY1 |
j |
0 |
0 |
û |
|
|
Матрица рассеяния (3) позволяет сделать вывод о том, что данный НО является
сонаправленным и сигналы в выходных плечах сдвинуты по фазе относительно друг друга на постоянную величину, равную p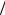 2 . Это является отличительной особенностью
2 . Это является отличительной особенностью
двухшлейфного НО.
Если нагрузить развязанный выход этого НО на согласованную нагрузку, то, как и в предыдущем случае, легко реализуется на его основе делитель мощности. В случае
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
возбуждения входа 1 (см. рис.2) мощность поступает на выходы 3 и 4, причем
коэффициент деления мощности связан с параметрами двухшлейфного НО следующим соотношением:
m = |
P3 |
= |
|
S13 |
|
|
2 |
= |
1 |
= |
1 |
. |
|
|
|
|
|||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
P4 |
|
|
S |
|
|
2 |
|
Y12 |
|
Y22 -1 |
||
|
|
|
|
|
|||||||||
|
|
|
14 |
|
|
|
|
|
|
|
|
||
Отсюда
|
|
|
|
|
|
Y 2 |
= |
|
1 |
|
|
и Y 2 = |
m +1 |
, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
m |
|
|
|
2 |
|
|
|
m |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
матрица рассеяния имеет следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
0 |
0 |
|
|
|
|
j |
1 |
|
|
ù |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ú |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
0 |
0 |
|
|
|
|
|
|
j |
ú |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
[S] |
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
ú |
|
|
|||||||||
|
|
= - |
|
|
|
|
|
|
|
ê |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
ú . |
|
|
||||||||||
|
|
|
m +1 |
|
|
j |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
ú |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
1 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
j |
0 |
|
|
|
0 |
|
|
ú |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
||
В |
частном |
случае |
|
|
|
гибридного |
двухшлейфного |
мостового |
НО |
||||||||||||||||||||||||||||
(m = 1) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S13 |
= |
S14 |
|
|
|
|
|
или Y1 = 1, |
|
Y2 = |
|
2. |
|
|
|
|
||||||||||||||||||
Проектирование развязанного кольцевого делителя мощности |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Λ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
B |
|
|
|
|
ρ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ρ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ρ0 |
|
|
|
|
C |
|
ρ1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Λ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис.3. Топология развязанного кольцевого делителя мощности
Равномерное деление мощности. Наиболее широкое распространение в СВЧ-технике получил развязанный кольцевой делитель мощности (рис.3). Его основные достоинства по сравнению с вышеприведенными делителями мощности - малые габариты, простота изготовления, меньшее количество входов. Он не требует применения согласованной нагрузки. В СВЧ-технике по отношению к нему применяется термин “бинарный делитель мощности”. Существенным его недостатком является то, что он делит мощность, поступающую на вход 1, только пополам.
Принцип действия этого делителя заключается в следующем. Если возбуждается вход 1 (см. рис.3), то в силу симметрии сигнал поровну делится между плечами 2 и 3, при этом точки В и С эквипотенциальны и через сопротивление R ток не идет.
Пусть теперь сигнал поступает в плечо 2, тогда в точку С он попадает через сопротивление R и через два четвертьволновых отрезка ВА и АС, т.е. в противофазе. При определенном выборе R и r1 относительно r0 можно обеспечить равенство по амплитуде
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
двух указанных сигналов и, следовательно, полную компенсацию энергии в точке С. Таким образом, плечи 2 и 3 будут развязаны. При этом половина мощности поступает в плечо 1, а половина рассеивается на сопротивлении R.
Выбор значений R иρ производится из известных коэффициентов матрицы рассеяния данного шестиполюсника. Воспользуемся только четырьмя коэффициентами:
|
1 - 2Y |
2 |
|
|
|
|
|
|
|
1 |
æ |
1 - 2Y |
2 |
|
1 - Y |
ö |
|||||||
S11 = |
1 |
; S22 = S33 = |
|
|
|
|
ç |
|
|
|
1 |
+ |
|
2 |
÷ |
||||||||
1 + 2Y |
2 |
2 |
ç |
1 + 2Y |
2 |
1 + Y2 |
÷; |
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
1 |
|
|
|
ø |
||
|
|
|
|
|
1 |
æ |
1 - 2Y 2 |
|
|
1 - Y |
ö |
|
|
|
|
|
|
||||||
|
S |
23 |
= |
|
ç |
|
1 |
|
- |
|
|
|
2 |
÷ |
, |
|
|
|
|
|
|||
|
2 |
1 + 2Y 2 |
1 |
+ Y2 |
|
|
|
|
|
||||||||||||||
|
|
|
ç |
|
|
÷ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
è |
1 |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
где Y1 = r0 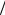 r1 и Y2 = 2r0
r1 и Y2 = 2r0 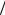 r1 .
r1 .
Идеальное согласование трех плеч делителя (S11 = S22 = S33 ) и идеальная развязка плеч делителя 2 и 3 (S23 = 0) получаются при следующих значениях:
Y = |
1 |
,Y = 1 или |
r |
= r |
|
|
и R = 2r |
|
. |
|
|
2 |
|
||||||||
|
|
|
|
|||||||
1 |
2 |
2 |
1 |
|
0 |
1 |
0 |
|
||
|
|
|
|
|
|
|
|
|
||
Неравномерное деление мощности. Схема кольцевого делителя мощности с развязанными выходами, способного обеспечить неравномерное деление мощности,
показана на рис.4. |
θ2 |
θ4 |
2 |
|
|||
|
|
|
|
|
ρ2 |
ρ4 |
ρ0 |
|
|
||
|
|
|
|
|
1 |
|
|
|
ρ0 |
R |
|
|
ρ3 |
ρ5 |
3 |
|
|
||
|
|
|
ρ0 |
|
θ3 |
θ5 |
|
Рис.4. Топология кольцевого делителя мощности с неравномерным делением мощности
Электрические длины линий передач делителя равны
q2 |
= |
|
2p ´ l2 |
, l2 = L2 4; |
||
|
|
|
||||
|
|
|
L2 |
|||
q3 |
= |
|
2p ´ l3 |
|
, l3 = L3 4; |
|
|
|
|||||
|
|
|
L3 |
|||
q4 |
= |
|
2p ´ l4 |
, l4 = L4 4; |
||
|
|
|
||||
|
|
|
L4 |
|||
q5 |
= |
|
2p ´ l5 |
, l5 = L5 4. |
||
|
|
|||||
|
|
|
L5 |
|||
Ели задать коэффициент деления по напряжению Ku = U2 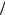 U3 , то волновые
U3 , то волновые
сопротивления отрезков линий передачи делителя можно записать в виде r2 = r0 
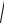 Ku (1 + Ku )2 ; r3 = r0
Ku (1 + Ku )2 ; r3 = r0 
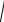 (1 + Ku2 )
(1 + Ku2 )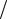 Ku ; r4 = r0
Ku ; r4 = r0 
 Ku ;
Ku ;
r5 = r0 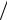

 Ku ,
Ku ,
асопротивление - как R = r0 (1+ Ku2 )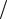 Ku .
Ku .
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
Пример. Определить геометрические параметры делителя в виде кольцевого НО с коэффициентом деления мощности m = 4 на МПЛ с поликоровой подложкой толщиной h = 1 мм, ε = 9,8; частота f = 5 ГГц; входное сопротивление ρ0 = 50 Ом.
Решение. 1. Из соотношений (1) и (2) определим значения нормированных проводимостей Y1 и Y2 (см. рис.1):
|
|
|
|
|
|
Y = 4 |
≈ 0,894; |
Y = 1 |
≈ 0,447, |
||
1 |
5 |
|
2 |
5 |
|
|
|
|
|
||
отсюда. ρ = ρ0 ≈ 56 Ом; |
ρ |
2 |
= ρ0 |
≈ 112 Ом. |
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
Y1 |
|
|
|
Y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
Воспользуемся графиками зависимости W от ρ и |
|
εэф |
от h, откуда определим |
|||||||||||||||||||
|
|
|
|
|
|
W0 ≈ 0,98 мм; |
W1 ≈ 0,7 мм; |
W2 ≈ 0,09 мм; |
|||||||||||||||
|
|
|
|
|
|
|
εэф |
0 |
= 2,54; |
|
|
εэф |
1 |
= 2,53; |
|
εэф |
2 |
= 2,48. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
Используя зависимость |
Λ = λ |
|
|
, |
определим соответствующие длины волн в |
|||||||||||||||||
|
εэф |
||||||||||||||||||||||
линиях передачи: |
|
|
|
Λ0 ≈ 2,36 см; |
Λ1 ≈ 2,37 см; |
Λ2 ≈ 2,42 см . |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
4. |
Определим длину отрезков линий кольца: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
l1 = Λ1 |
4 = 5,9 мм; |
l2 = Λ2 4 = 5,9 мм; l3 = 3Λ1 4 = 17,7 мм . |
|||||||||||||||||||
5. |
Рассчитаем средний, внутренний и наружный диаметры кольца: |
||||||||||||||||||||||
|
|
d |
ср |
= |
l1 + 2l2 + l3 |
=11,26 мм; d |
вм |
= d |
ср |
− W =10,56 мм; |
|||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dн = dср + W1 =11,96 мм .
Задание 1. Определить геометрические параметры делителя в виде: а) кольцевого и б) двухшлейфного НО с коэффициентом деления мощности m = 3 на МПЛ с поликоровой подложкой толщиной h = 0,5 мм (ε = 9,8; частота f = 2 ГГц; входное волновое
сопротивление
ρ0 = 50 Ом).
Задание 2. Определить геометрические параметры кольцевого делителя мощности с коэффициентом деления мощности m = 2 и m = 4 на МПЛ с поликоровой подложкой толщиной h = 0,5 мм (ε = 9,8; частота f = 8 ГГц; входное волновое сопротивление ρ0 = 50 Ом).
Литература
1. Малорацкий Л.Г. Микроминиатюризация элементов и устройств СВЧ. - М.: Сов.
радио, 1976. - С. 157 - 170.
2. Чистюхин В.В. Антенно-фидерные устройства. - М.: МИЭТ, 1997. - С. 17 - 34.
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
