
- •Проектирование антенно-фидерных устройств
- •Методические указания к практическим занятиям по курсу “Антенно-фидерные устройства”
- •Введение
- •Список употребляемых сокращений
- •Семинар № 1. Расчет основных параметров МПЛ
- •Семинар № 2. Определение матриц рассеяния элементарных многополюсников
- •Семинар № 4. Проектирование делителей мощности
- •Семинар № 5. Проектирование коммутаторов и фазовращателей
- •Семинар № 6. Расчет характеристик системы линейных вибраторов и антенн бегущей волны
- •Семинар № 7. Способы возбуждения симметричных вибраторов
- •Семинар № 8. Рупорные антенны
- •Семинар № 9. Расчет линзовых антенн
- •Семинар № 10. Расчет антенн поверхностных волн
- •Семинар № 11. Проектирование линейной ФАР с заданным уровнем боковых лепестков
- •Семинар № 12. Эффективность параболических зеркальных антенн
- •Семинар № 13. Проектирование передающих АФАР
- •Семинар № 14. Проектирование приемных АФАР. Расчет их энергетических параметров
- •Семинар № 15. Влияние амплитудно-фазового разброса на энергетические характеристики АФАР
- •Семинар № 16. Проектирование микрополосковых антенн
- •Семинар № 17. Адаптивные антенные решетки
Семинар № 16. Проектирование микрополосковых антенн
Тенденция к микроминиатюризации радиоэлектронной аппаратуры обусловила необходимость использования печатных микрополосковых антенн. МПА, изготовленные по технологии ГИС, обеспечивают высокую повторяемость размеров, низкую стоимость, минимальные массогабаритные характеристики и малую металлоемкость. Для сравнения:
турникетная антенна на полуволновом вибраторе с рефлектором имеет массу порядка 200 ÷ 300г, аналогичная МПА - порядка 30 г. Подобные сравнения применимы и к занимаемой площади.
МПА способны излучать энергию с линейной, круговой и эллиптической поляризацией, допускают удобные конструктивные решения для обеспечения работы в двух- или многочастотных режимах, легко позволяют объединить несколько элементарных излучателей в один и разместить их на поверхности сложной формы. Кроме того, МПА обладают высокими аэродинамическими, механическими и температурными характеристиками.
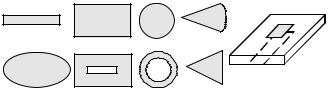
В настоящее время применяется большое число типов элементарных излучателей полосковой конструкции и антенных структур на основе объединения однотипных и разнотипных ЭИ в единой антенной системе. Для примера на рис.1 изображено несколько типов МПА.
Рис.1. Типы микрополосковых антенн
Разнообразие форм свидетельствует о сложности теоретического анализа таких электродинамических структур. Переход от стандартных форм ЭИ к усложненным
геометрическим формам позволяет одновременно решить задачу согласования активной и компенсацию реактивной компонент входного сопротивления ЭИ, обеспечить необходимую поляризацию излучения, удобство сочетания ЭИ в антенной решетке и многое другое. Кроме того, необходимо учитывать, что переход к объемным ИС
представляет для МПА целый ряд интересных возможностей использования третьего измерения. При этом, например, входной полосовой фильтр приемного устройства можно связывать непосредственно с ЭИ или их группой, разводить (поэтажно) входы многоканального устройства с минимумом коммутационных линий, существенно уменьшать паразитное излучение питающих фидеров и т.д. Разумеется, конструкция ЭИ при этом становится трехмерной, и соответственно возрастают трудности ее адекватного описания, составление удобной математической или электродинамической ее модели.
Теория простейшего прямоугольного микрополоскового излучателя (рис.2,а) достаточно сложна. Однако ряд оценочных результатов можно получить на простой модели в виде конечного отрезка регулярной ЛП.
Основное предположение заключается в том, что прямоугольная полосковая антенна представляет собой элементарную антенную решетку из двух излучателей - двух открытых концов МПЛ (рис.2,б). Эти излучатели соединены между собой отрезком регулярной низкоомной ЛП длиной примерно L ≈ Λ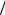 2 (в общем случае L ≈ n Λ
2 (в общем случае L ≈ n Λ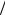 2 , n = 1,2,Κ
2 , n = 1,2,Κ
, где Λ - длина волны в регулярной МПЛ) и шириной W. Достоинство такого подхода - простота и наглядность модели, недостаток заключается в том, что эта модель применима только к ЭИ прямоугольной формы.
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

|
W |
d |
|
ρ0 |
|
|
|
|
|
|
|
|
|
W |
|
ε |
d |
|
L |
|
L |
б) |
в) |
|
а) |
Рис.2. Прямоугольная МПА: а - проекция МПА; б - эквивалентная схема МПА в виде двух щелевых антенн; в - распределение полей и токов по МПА
При построении модели МПА в виде отрезка эквивалентной ЛП предполагается, что ЭИ можно рассматривать в виде одномерной резонирующей структуры, не имеющей вариаций электромагнитного поля по толщине и ширине элемента. При этом предполагается, что в линии распространяется квазиТ-волна и что электромагнитное поле полностью сосредоточено под полосковым проводником шириной W. Если волна, падая на разомкнутый конец ЛП, целиком отражается от него, то данная неоднородность представляет для падающей волны чистую реактивность. Свободный конец линии имеет потери на излучение и преобразует падающую волну в поверхностную волну подложки. Поэтому его можно описать через эквивалентную проводимость G + jB в виде
параллельного соединения активной проводимости G, учитывающей потери на излучение и преобразование, и реактивной проводимости B, учитывающей реактивную энергию поля, запасаемую вблизи неоднородности в высших нераспространяющихся типах волн, возникающих при падении основной волны на край структуры. Для эффективного санкционированного излучения требуется, чтобы излучатель был резонансным, т.е. его эффективная длина должна составлять целое число полуволн в структуре L » n L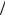 2 .
2 .
Рассмотрим случай n = 1.
Распределение краевых электрических полей МПА представлено на рис.2,в. Поскольку длина ЭИ L приблизительно равна L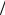 2 , то нормальные составляющие этих
2 , то нормальные составляющие этих
полей (продольные кромки) находятся в противофазе, а возбуждаемые ими поля излучения в направлении, поперечном к плоскости ЭИ, уничтожаются. Эти составляющие дают малый вклад в излучение и в дальнейшем не учитываются. Тангенциальные
составляющие полей у больших краев синфазны и в поперечном направлении формируют максимум излучения. В результате прямоугольный ЭИ представляется в виде двух гипотетических синфазно возбуждаемых щелевых источников, расположенных в металлическом основании, с равномерным распределением электрического поля вдоль поверхности каждой щели (рис.2,в). Ширина щелей принимается равной толщине d подложки, их длина равна W, а расстояние между щелями L » L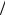 2 . Дальнейшее
2 . Дальнейшее
определение характеристик ЭИ проводится по стандартной процедуре анализа апертурных антенн.
Рассмотрим характеристики излучения одиночной щели. Компоненты электрического поля определяются из следующих соотношений:
|
|
|
|
|
|
Eθ = 0 ; |
|
|
|
|
||
|
|
e− jk0r |
|
sin[(k |
0 |
d 2)sin qcos j]sin[(k W 2)cos q] |
|
|||||
Eϕ = - jU 0 k0W |
|
|
|
|
|
|
|
0 |
|
. |
||
2pr |
|
|
(k0d 2)sin qcos j(k0W 2)cos q |
|||||||||
|
|
|
|
|
||||||||
Проводимость излучения щели: |
|
|
|
|
|
|
|
|
|
|
||
|
ì (W 2l0 )2 ×10−1, |
W l0 < 0,35; |
|
|||||||||
G = |
ïW 120l |
0 |
-1 60p2 , |
W l |
0 |
Î(0,35 ¸ 2); |
|
|
||||
|
í |
|
|
|
|
|
|
|
|
|||
|
ï |
|
|
W 120l0 , |
W l0 > 2. |
|
||||||
|
î |
|
|
|
||||||||
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Пусть L - эквивалентное линейное удлинение ЭИ на каждом из его концов, тогда эквивалентная реактивная проводимость определяется как B = wC = Y0 tg(hDL)» Y0hDL , где
h = 2p
 eэф
eэф  l0 ; Y0 - волновая проводимость МПЛ,
l0 ; Y0 - волновая проводимость МПЛ,
|
|
|
Y = |
|
|
|
1 |
|
|
ìW |
|
+1,393 + 0,667 lné |
W |
+ 1,444ùü |
для |
W |
>>1. |
|||||||
|
|
|
e |
|
|
|||||||||||||||||||
|
|
|
эф |
|
|
|
í |
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
ê |
|
|
úý |
|
|
d |
|
||||
|
|
|
|
|
|
120p î d |
|
|
|
ë d |
ûþ |
|
|
|
||||||||||
Значение |
L можно аппроксимировать следующей формулой: |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
DL |
|
= 0,412 |
eэф + 0,3 |
|
W + 0,264d |
, |
|
(1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
eэф - 0,258 |
W + 0,8d |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
é |
|
æ |
|
|
|
d ö |
− |
|
1 ù |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где e |
эф |
= |
0,5êe +1 + (e -1)ç1 |
+12 |
|
|
÷ |
|
|
|
|
ú . |
|
|
|
|
(2) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ê |
|
è |
|
|
W ø |
|
|
|
|
ú |
|
|
|
|
|
|
|
|
||||
|
|
|
ê |
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|||||
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
Для расстояний, не очень близких к центру ЭИ, полная входная проводимость ЭИ
определяется формулой |
2G |
, где x0 |
- расстояние от одного из концов |
Y1(x0 )» cos2 (nx ) |
0
линейного резонатора до точки запитки.
Значение ширины ЭИ определяется из соотношения
|
|
|
|
с ée +1ù− |
1 |
|
|||
|
W = |
|
|
2 |
; |
||||
|
|
|
|
ê |
ú |
|
|||
|
|
|
|
|
|||||
|
|
2 fp ë |
2 û |
|
|
||||
L = |
с |
|
|
|
|
± 2DL . |
|
|
|
2 fp |
|
|
|
|
|
|
|||
|
e |
|
|
|
|||||
|
|
эф |
|
|
|
||||
Диаграмма направленности ЭИ в Е-плоскости имеет вид:
|
|
F |
|
= |
sin u |
cos uL |
, |
|
u = |
k0d |
cos q, |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
E |
|
|
u |
|
|
|
d |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в Н-плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin v |
|
|
|
|
|
|
|
k0W |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
= |
|
sin q, v = |
cos q . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
v |
|
|
|
|
|
|
|
|
2 |
|
|
|
||
Ширина ДН в Е-плоскости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
ì7,03[3(k |
|
|
|
|
|
]−1 ü |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
Dq |
E0,5 |
= 2 cos−1 |
0 |
L)2 |
+ (k W )2 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
|
|
|
|
|
0 |
ý |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
é |
|
|
|
k W |
ù |
− |
1 |
ü |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 cos−1 |
ï |
|
|
|
2 |
ï |
|
|
|
|
|
|
|
|||||||||
в Н-плоскости: Dq |
|
|
|
= |
í2 1 |
|
+ |
|
0 |
|
|
|
|
ý . |
|
|
|
|
|
|
|
|||||||||
H 0,5 |
|
ú |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ï |
ê |
|
|
2 |
ï |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
û |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
Добротность ЭИ: Q = Qизл |
Rп |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Rизл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
где Qизл = (с |
|
) 4 fp d ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
eэф |
Rп = Rизл + Rд + Rом , |
|
|
|
|
|
|
|
||||||||||||||||||||||
здесь Rизл =1 G ; Rом = 0,00027 |
|
Qизл2 (L W ). |
|
|
|
|
|
|
|
|||||||||||||||||||||
fp |
|
|
|
|
|
|
|
|||||||||||||||||||||||
В диэлектрике: h = |
Rизл |
´100% , где η - КПД излучателя. |
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Rп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ширина полосы частот:
(3)
(4)
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

|
DW = |
S - |
1 |
|
, где KстU < S . |
|
|
|
|
|
|||
|
|
|||||
|
|
Q S |
|
|||
Для определения КНД применяют следующие формулы: |
||||||
D » 6,6 |
при W << l0 ; D » |
8W при W >> l0 . |
||||
|
|
|
|
|
|
l0 |
Коэффициент усиления: Gэф = hD . |
|
|||||
Пример. Определить |
геометрические |
параметры МПА для частоты |
||||
fp = 6 ГГц, e = 9,8, d =1мм .
Решение. 1. Воспользуемся формулой (3) для определения ширины излучателя (см.
рис.2):
|
3 ×108 |
|
|
|
é9,8 +1ù |
− |
1 |
|
|
|
|
|
|
|
|
|
|
||
W = |
|
|
2 |
|
= 0,0107 м |
=10,7 мм . |
|||||||||||||
2 × 6 ×10 |
9 |
ê |
2 |
ú |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ë |
û |
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. По формуле (2) рассчитаем значение eэф : |
|
|
|
|
|
|
|
|
|||||||||||
|
é |
|
|
|
|
|
|
|
æ |
|
|
1 |
ö |
− |
1 |
ù |
|
||
|
ê |
|
|
|
|
|
|
|
|
|
|
2 |
ú |
|
|||||
eэф = 0,5ê9,8 |
+ |
1 + |
(9,8 - |
1)ç1 |
+12 |
|
|
÷ |
|
|
ú |
» 8,42 . |
|||||||
10,7 |
|
|
|||||||||||||||||
|
ê |
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
ú |
|
|||
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
3. В нашем случае характер торцевой нагрузки емкостной, поэтому предварительно рассчитываем по формуле (1) значение L :
DL = 0,412 8,42 + 0,3 10,7 + 0,264 » 0,42 мм 8,42 - 0,258 10,7 + 0,8
и по формуле (4) - значение длины излучателя (из-за характера нагрузки в формуле берем знак “−”):
L = |
|
3 ×108 |
- 2 × 0,42 ×10 |
−3 » 7,78 мм. |
|
|
× 6 ×109 |
× 2,9 |
|||
2 |
|
|
|||
Задание 1. Рассчитать геометрические параметры микрополос-ковой прямоугольной
антенны и определить точку подключения подводящей линии с волновым сопротивлением r0 =100 Ом на частоте fp = 4 ГГц, e = 2,6, d = 2 мм.
Задание 2. Рассчитать геометрические параметры и электрические характеристики
(ширину |
ДН, |
добротность |
и КНД) прямоугольной МПЛ на частоте |
fp = 2,5 ГГц, |
e = 9,8, |
tg d »10−4 ; |
d =1мм. |
Литература
1. Нефедов Е.И., Козловский В.В., Згурский А.В. Микрополосковые излучающие и резонансные устройства. - Киев: Техника, 1990. - С. 95 - 124.
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
