Семинар № 14. Проектирование приемных АФАР. Расчет их энергетических параметров
Энергетический потенциал приемных АФАР определяется соотношением
Ппрм = S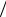эф 
Tэф ,
где Sэф - эффективная площадь антенны; Tэф - шумовая температура АФАР (в градусах
Кельвина), приведенная к раскрыву решетки.
Эффективная площадь АФАР связана с ее геометрической площадью S через коэффициент использования поверхности σ , определяемый в свою очередь амплитудно- фазовыми характеристиками ее тракта, требуемым уровнем боковых лепестков и допустимыми потерями потенциала на краях сектора сканирования A: Sэф = SσA .
Значение σ изменяется, как правило, от 0,1 до 0,8 и определяется сектором сканирования решетки и соответственно ДН ее элементов, значение A обычно равно 1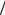
2 .
Тогда Sэф = 12 Sσ .
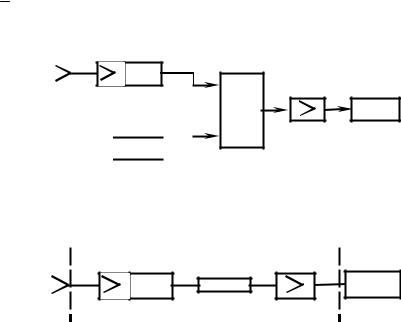
Простейшая структурная схема приемной АФАР приведена на рис.1. kш1,k p1
ФВ |
kш 2 |
,k p2 |
|
ΣN |
ПРМ |
ФВ 
|
Рис.1. Структурная схема приемной АФАР |
T0 |
Tпрм |
k |
|
,k p1 |
k |
|
,k |
p2 L3 |
|
L1 |
ш1 |
ФВ |
L2 |
ш 2 |
|
ПРМ |
|
|
|
|
|
|
|
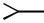
Рис.2. Структурная схема приемного канала АФАР
Для вычисления Tэф необходимо изобразить путь прохождения |
сигнала от |
каждого канала до приемника (рис.2). На рис.2: |
|
- величина L1 определяется потерями в соединительном кабеле (излучателя с МШУ), |
|
потерями в фильтре на входе МШУ, сумма которых обычно составляет |
0,5 ÷1,5 дБ ( |
1,1 ÷1,4 отн. ед.); |
|
-значение kш1 ≈ kш2 (условие стандартизации и унификации) определяется
коэффициентом шума МШУ и имеет достаточно широкий диапазон значений - от 1 до 7 дБ (1,25 ÷ 5 отн. ед.);
- |
значение |
k р1 ≈ k р2 (коэффициенты |
усиления соответствующих МШУ на рис.2) |
составляет обычно 15 ÷ 30 дБ ( 30 ÷1000 отн. ед.); |
|||
- |
величина |
L2 включает потери в |
фазовращателе, юстировочном фазовращателе, |
сумматоре и соединительных кабелях, обычно L2 составляет3 ÷ 5 дБ ( 2 ÷ 3 отн. ед.);
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
- величина L3 , равная примерно 0,5 дБ (1,1 отн. ед.), определяется потерями в
соединительном кабеле;
- значение Tпрм (собственная шумовая температура приемника, К) достигает величины
1000 К.
Для схемы приемной АФАР, изображенной на рис.1, эффективная шумовая температура, приведенная к ее входу, определяется формулой
|
|
|
|
pвх |
|
|
= T (L -1)+ T |
(k |
|
|
-1)+ T |
(L |
2 |
-1)L |
|
|||||||||||||||
T = |
|
ш |
|
|
ш1 |
|
|
1 |
|
+ |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
эф |
|
kDf |
|
|
0 |
1 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
k р1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ T |
|
(kш 2 -1)L1L2 |
+ T |
(L3 −1)L1L2 |
+ T |
|
L1L2 L3 |
, |
|
(1) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
0 |
|
|
|
k р1 |
|
|
0 |
|
|
k р1k р2 |
|
|
|
|
прм |
|
k р1k р2 |
|
||||||||||||
где pшвх - мощность |
|
шума |
|
|
на |
входе |
|
АФАР, |
Вт; |
|
k |
|
- постоянная Больцмана, |
|||||||||||||||||
k =1,38 ×10−23 Дж К ; f - рабочая полоса частот, Гц. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Преобразуем формулу (1) к следующему виду: |
|
|
|
|
|
|
|
|||||||||||||||||||||||
T = T |
(k |
ш1 |
L -1)+ T |
(L2 -1)L1 |
|
+ T |
0 |
(kш 2 -1)L1L2 |
|
+ |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
эф |
0 |
|
|
|
1 |
|
0 |
|
|
k р1 |
|
|
|
|
|
|
|
|
k р1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
+ T |
(L3 −1)L1L2 |
+ T |
|
|
|
L1L2 L3 |
. |
|
|
|
|
(2) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
k р1k р2 |
|
|
прм |
|
k р1k р2 |
|
|
|
|
|
|
|
||||||||
Из анализа формулы (2) с учетом проведенных выше оценок составляющих ее величин можно сделать следующие выводы. При больших значениях коэффициента усиления МШУ ( k p »100 ¸1000 ) наибольший вклад в Tэф вносят коэффициент шума
МШУ, который однозначно определяется kш используемого транзистора, и потери L1 ,
связанные с потерями в соединительном кабеле и фильтре на входе МШУ. Тогда, по сути, можно использовать для расчетов только первые три члена суммы:
|
|
|
|
|
|
|
|
|
|
Tэф = T0 (kшΣ -1), |
||
где k |
шΣ |
= k |
ш1 |
L |
+ |
(L2 -1)L1 |
+ |
(kш 2 -1)L1L2 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
k р1 |
|
k р1 |
|
|
||||
|
|
|
|
|
|
|
|
|
||||
Остальные |
два слагаемых |
пренебрежимо |
малы. Кроме того, при значениях |
|||||||||
k p1 » 500 ¸1000 |
можно с |
достаточной степенью |
точности |
считать, что kшΣ » kш1L1 и |
||||||||
Tэф = 290(kш1L1 -1) [К]. |
|
|
|
|
|
|
||||||
|
|
Однако при значениях |
k р1 » k р2 » 10 ¸15 |
дБ (10 ÷ 30 |
отн. ед.) такое упрощение |
|||||||
формулы (2) уже недопустимо. В этом случае существенную роль будут играть потери в ФВ и сумматоре. Проведем следующее вычисление:
|
|
|
|
k |
|
L L |
2 |
|
L |
|
|
æ |
|
L |
2 |
ö |
||
k |
шΣ |
= k |
L + |
|
ш1 1 |
- |
|
1 |
» k |
L |
ç1 |
+ |
|
|
÷ . |
|||
|
|
|
k |
|
k |
|
|
|||||||||||
|
|
ш1 1 |
|
k |
|
|
|
|
|
ш1 1 |
ç |
|
|
|
÷ |
|||
|
|
|
|
|
|
р1 |
|
|
|
р1 |
|
|
è |
|
|
р1 |
ø |
|
Пример. Рассчитать эффективную шумовую температуру на входе приемной АФАР, имеющей следующие параметры входящих в нее блоков и устройств: потери в кабеле от излучателя до модуля L1′ » 0,3 дБ; потери в полосе пропускания полосно-
пропускающего фильтра на входе модуля L′′ » 0,7 дБ; коэффициент шума МШУ k |
ш |
£ 2 дБ; |
1 |
|
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
коэффициент усиления МШУ k р ³ 20 дБ в рабочей полосе частот; суммарные потери в выходном тракте приемного канала L2 » 4 дБ.
Решение. С учетом того, что значение k р МШУ достаточно велико, для расчета Tэф воспользуемся выражениями (3) и (4). В формулу (4) подставим значение L1 = L1′ + L1′′ =1 дБ. Прежде чем производить расчеты, необходимо все заданные величины перевести в разы. Тогда L1 »1,25; kш »1,58 ; k р »100 ; L2 » 2,5 . Значение kшΣ будет равно
kшΣ =1,58 ×1,25 + (2,5100-1) ×1,25 » 2.
Окончательно Tэф = 290 × (2 -1)= 290 К.
Задание. Спроектировать приемную АФАР с сектором сканирования Dqск = ±25ο
на частоте f = 5,3 ГГц, |
обладающую |
энергетическим потенциалом Ппрм ³ 4 см2 К . |
Ширина главного лепестка Dq0,5 » 4,5ο , |
уровень боковых лепестков t ≤ −17 дБ, параметры |
|
МШУ: k р ³17 дБ и kш £ 2,5 |
дБ. Нарисовать схему проектируемой АФАР и обосновать ее. |
|
Примечание: при проектировании использовать материалы семинара №13.
Литература
1. Чистюхин В.В. Антенно-фидерные устройства. - М.: МИЭТ, 1997. - С. 193 - 201.
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
Семинар № 15. Влияние амплитудно-фазового разброса на энергетические характеристики АФАР
Особенности дискретного фазирования элементов. Известно, что при создании
современных АФАР для управления положением луча используются дискретные фазовращатели, с помощью которых фаза возбуждения в каждом излучателе может быть изменена только скачком на величину ΔΦ , называемую дискретом фазирования. Обычно
DF = 2p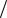
2 p , где p - целое число, определяющее количество разрядов фазовращателя.
Важнейшим преимуществом дискретного фазирующего устройства по сравнению с плавным (аналоговым) является улучшенная стабильность. Это объясняется тем, что
управляющие устройства работают в режиме переключения с использованием только двух крайних областей их характеристик. Другим преимуществом дискретного фазирующего устройства является удобство управления им с помощью ЭВМ.
При дискретном фазировании решетки в направлении q0 , j0 для каждого излучателя рассчитывается точное (идеальное) значение фазы Fп0 по формуле
Fп0 = -k(dxn sin q0 cos j0 + dyn sin q0 sin j0 ),
где k = 2p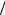
l - волновое число; dxn , dyn - координаты n-го излучателя в решетке. Заметим, что идеальное значение Fп0 округляется до ближайшего дискретного
значения Fп :
Fп = DFEæç0,5 + Fп0 DFö÷ = Fп0 - dFп ,
èø
где E(x) - операция выделения целой части числа x; dFп = dFп (Fп0 )= Fп0 - Fп - систематическая фазовая ошибка из-за дискретности фазирования, зависимость этой ошибки от значения “идеальной” фазы Fп0 представляет функцию с периодом ΔΦ (см.
[1], стр. 206, рис.2.81).
С учетом вышесказанного множитель направленности любой дискретно-
фазируемой решетки может быть представлен в виде
N
F(q, j)= å In e j(φn +Φпо )e− jδΦп , n=1
где fп = -k(dxn sin qcos j + dyn sin qsin j).
После ряда преобразований [1] выражение для множителя решетки принимает
вид
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
F(q,j)= åСmFΣm (q,j), |
|||
|
|
|
|
|
m=−∞ |
|
|
|
N |
|
|
||||||
где FΣm (q,j)= å |
|
In |
|
exp{j[fn + Fпо (1+ 2pm DF)]}, |
(1) |
|
||
|
|
|
||||||
n=1 |
|
|
|
Cm = |
(-1)m sin(DF 2) |
. |
|
(2) |
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
(DF 2)+ mp |
|
|
|
Этот множитель представляет собой бесконечную сумму |
парциальных ДН FΣm (q,j), |
|||||||
главный вес в которой имеет нулевой член FΣ0 (q,j), |
характеризующий ДН решетки с |
|||||||
идеальным фазированием. Однако главный максимум |
этой ДН уменьшен в |
|||||||
С0 = (sin(DF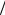
2))
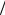(DF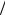
2) раз, что свидетельствует о снижении коэффициента направленного
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
действия. Другие слагаемые в (1) дают дополнительное паразитное излучение из-за дискретности фазирования. С уменьшением дискрета фазы до нуля интенсивность паразитных составляющих стремится к нулю.
Паразитные лепестки заметного уровня характерны лишь для линейных и плоских АФАР с дискретным фазированием. В неплоских решетках происходит своеобразное рассеяние мощности паразитных ДН в широкой зоне углов. Аналогичного
эффекта можно добиться для линейных и плоских решеток путем создания нелинейного начального фазового распределения - фазовой подставки. Естественно, что начальное фазовое распределение должно компенсироваться ФВ при сканировании.
Снижение коэффициента использования поверхности АФАР с дискретным фазированием описывается приближенной формулой
|
|
A = |
sin2 |
(DF 2) |
, |
|
|
|
|
|
DF 2 |
|
|
|
|||
|
|
|
|
|
|
|
||
справедливой как при наличии начальной фазовой подставки, так и при ее отсутствии. |
|
|||||||
Пример. |
Рассчитать |
уровень |
|
паразитных |
максимумов |
при |
||
m = 1; ±2 в плоской АФАР для величин дискрета фазирования DF = p 2; p 4 . |
|
|||||||
Решение. Абсолютный уровень паразитных максимумов определяется значением коэффициента Cm (см. формулу (2)). Подставив в выражение (2) заданные значения m и
ΔΦ , рассчитаем искомые величины, которые сведем в таблицу (расчеты проведем по мощности):
|
m |
|
|
|
ΔΦ |
|||
|
p 2, дБ |
|
|
|
p 4, дБ |
|||
|
|
|
|
|
||||
|
1 |
А1 = -10,4 |
|
|
|
А1 = -15,8 |
||
|
−1 |
А−1 = -14,9 |
|
|
|
А−1 = -20,2 |
||
|
2 |
А2 = -20 |
|
|
|
А2 = -24,8 |
||
|
−2 |
А−2 = -17,8 |
|
|
|
А−2 = -23,7 |
||
Значение Аm |
|
|
|
|
|
|
|
|
вычисляется |
по формуле |
|
|
|
|
|||
|
|
А = 10lg |
|
C |
m |
|
2 . |
|
|
|
|
|
|||||
|
|
m |
|
|
|
|
||
Рассмотрим несколько иной подход к учету влияния дискретного фазирования на энергетику АФАР. В ФВ, имеющем дискретность управления в p бит (разрядов), фаза может устанавливаться до нужной величины с остаточной ошибкой:
- максимальной фазовой a = ± p |
; |
|
|
|
|
|
|
|
|
|
|
2 p |
|
|
|
|
p |
|
|
|
|
|
|
- среднеквадратичной фазовой aскв |
= ± |
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
× |
2 p |
|
|
|
|
||||
|
|
3 |
|
|
|
|
|
||||
Анализ показывает, что уменьшение усиления |
|
G антенной решетки может быть |
|||||||||
рассчитано по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
DG » aскв2 |
= |
1 |
p2 |
. |
|||||
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
22 p |
||
Точность наведения луча при дискретном фазировании. В моноимпульсных
радиолокационных станциях точное определение направления на цель обеспечивается с помощью разностной ДН, следовательно, определенный интерес представляет оценка точности установки нулевого положения ДН. При использовании ФВ с квантованием
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com
фазы положение нуля может смещаться с дискретностью, зависящей от степени дискретности ФВ.
Для заданного направления сканирования q0 ошибка наведения луча антенной
решетки и соответственно нуля разностной диаграммы δθ |
может быть рассчитана по |
||||||
формуле |
|
|
4 |
|
2p |
|
|
dqcos q0 |
= |
|
|
, |
(3) |
||
p(d |
l)N 2 |
|
2 p |
||||
|
|
|
|
|
|||
где d - межэлементное расстояние в решетке; λ - рабочая длина волны; N - количество излучателей решетки в плоскости отклонения луча; p - количество разрядов используемого ФВ.
Уравнение (3) можно выразить через ширину луча с использованием известного
соотношения: Dq0,5ск = |
|
51οl |
, где |
Dq0,5ск |
- ширина луча антенной решетки в |
|||
|
dN cos q0 |
|||||||
направлении q0 . Тогда |
|
|
|
|
|
|
||
|
|
|
dq |
|
9 |
|
||
|
|
|
|
|
= |
. |
||
|
|
|
|
Dq0,5ск |
N × 2 p |
|||
Задание 1. Рассчитать уменьшение усиления АФАР, используя два подхода для величины дискрета ФВ: DF = p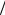
2; p
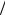4 .
Задание 2. Оценить точность выставки луча для АФАР со следующими параметрами:
Dq0,5X = 5ο; Dq0,5Y =1ο; q0 = ±30ο; l =10 см; p = 3 .
Литература
1. Чистюхин В.В. Антенно-фидерные устройства. - М.: МИЭТ, 1997. - С. 205 - 215.
PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com