
- •Модуляция цифровым сигналом
- •Частотная модуляция (манипуляция) Frequency Shift Keying (fsk))
- •– Длительность импульса, соответствующая одному биту,
- •Частотная модуляция (манипуляция) Frequency Shift Keying (fsk))
- •– Длительность импульса, соответствующая одному биту,
- •2. Фазовая манипуляция (Phase shift keying – psk)
- •Амплитудно-фазовая манипуляция
Модуляция цифровым сигналом
Частотная модуляция (манипуляция) Frequency Shift Keying (FSK))
При
частотной модуляции знаку «0» соответствует
частота
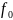 =
=
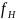 -
-
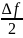 ,
знаку «1» - частота
,
знаку «1» - частота
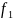 =
+
,
где
– несущая частота,
=
+
,
где
– несущая частота,
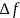 - сдвиг частот. Параметры модуляции FSK:
- сдвиг частот. Параметры модуляции FSK:
сдвиг (разность) частот = - ,
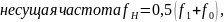
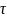 – длительность
импульса, соответствующая одному биту,
– длительность
импульса, соответствующая одному биту,индекс частотой модуляции m = .
При
аналоговом видеосигнале m
=
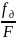 ,
где
,
где
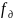 – девиация частоты, то есть, максимальное
отклонение частоты от несущей
,
F
– частота видеосигнала. При цифровом
видеосигнале девиация частоты
=
,
частота видеосигнала (тактовая частота)
– девиация частоты, то есть, максимальное
отклонение частоты от несущей
,
F
– частота видеосигнала. При цифровом
видеосигнале девиация частоты
=
,
частота видеосигнала (тактовая частота)
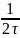 .
.
Допустим,
цифровое сообщение: 10011010 – рис. 1.
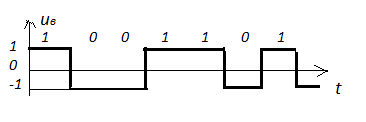
Рис. 1. Напряжение видеосигнала
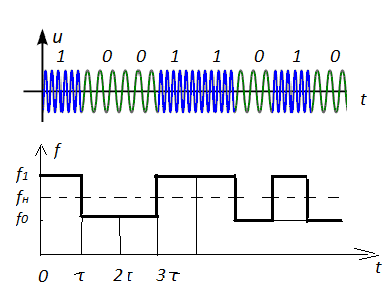
Рис. 2. Напряжение радиосигнала и зависимость частоты от времени.
На рис.2 представлен радиосигнал с частотной манипуляцией последовательность символов.
Спектр радиосигнала с частотой манипуляцией
На
рис. 3 показан спектр колебаний несущей
частоты, модулированной последовательностью
прямоугольных импульсов длительностью
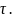 Огибающая спектральная плотности
мощности S(f)
подчиняется формуле
Огибающая спектральная плотности
мощности S(f)
подчиняется формуле
S
(f)
=
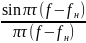 .
.
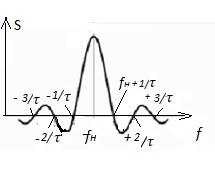
Рис. 3. Спектр колебаний частоты , модулированной непериодической последовательностью прямоугольных импульсов длительностью .
Спектр
радиосигнала с цифровой частотной
манипуляцией определяется как сумма
двух спектров. В процессе передачи
сообщений постоянно меняется частота:
или
.
Один спектр сосредоточен вблизи частоты
,
другой – вблизи частоты
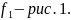
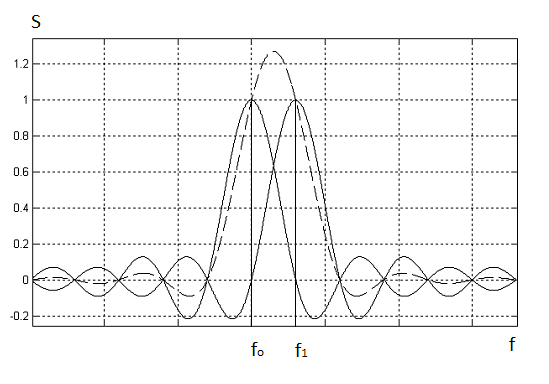
Рис. 4. Формирование спектра MSK сигнала
(S – спектральная плотность мощности).
Спектр
мощности радиосигнала одной частоты
содержит центральный лепесток шириной
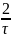 и
боковые лепестки ширин
и
боковые лепестки ширин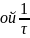 каждый. Суммарный спектр FSK
радиосигнала показан на рис.4 пунктиром.
Если выбрать сдвиг частот
=
каждый. Суммарный спектр FSK
радиосигнала показан на рис.4 пунктиром.
Если выбрать сдвиг частот
=
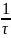 , то при суммировании спектров боковые
лепестки уменьшатся, при этом индекс
модуляции m
=1. Как следует из рис.1, ширина центрального
лепестка суммарного спектра при таком
индексе равна
, то при суммировании спектров боковые
лепестки уменьшатся, при этом индекс
модуляции m
=1. Как следует из рис.1, ширина центрального
лепестка суммарного спектра при таком
индексе равна
 .
.
Варианты частотной манипуляции
Частотная манипуляция с минимальным сдвигом MSK (Minimum shift keying).
Возникает
задача – нельзя ли уменьшить ширину
основного лепестка спектра путем
сближения частот
и
.
Рассмотрим, насколько близки могут быть
эти частоты, чтобы функции
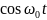 и
и
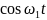 оставались независимы, то есть были
ортогональными. Условие ортогональности
функций
оставались независимы, то есть были
ортогональными. Условие ортогональности
функций
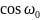 t
и
t
и
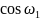 t:
t:
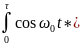 =
0.
=
0.
Решением этого уравнения является условие
= 0,5 F n, где n = 0, 1,2,…
Минимальный
сдвиг, при котором функци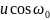 t
и
t
не коррелированы,
t
и
t
не коррелированы,
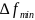 =
=
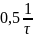 . В этом случае, индекс модуляции m
= 0.5.
. В этом случае, индекс модуляции m
= 0.5.
Можно
заметить, что ширина основного лепестка
спектра мощности радиосигнала MSK равна
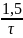 ,
в то время, как в модуляции FSK
ширина равна
.
,
в то время, как в модуляции FSK
ширина равна
.
На рис. 2 показано напряжение радиосигнала, в котором мгновенная фаза высокочастотных колебаний плавно изменяется с течением времени. Именно такого изменения фазы добиваются при формировании радиосигнала. В противном случае, при переключении частоты от к и обратно мгновенная фаза изменяется скачкообразно, что приводит к появлению в спектре радиосигнала высших гармоник этих частот и увеличению величины боковых лепестков. При желании подчеркнуть непрерывность фазы радиосигнала метод частотной манипуляции обозначают как CPFSK (Continuous phase FSK).
Гауссовская частотная манипуляция с минимальным сдвигом GMSK (Gaussian minimum Shift Keying)
При использовании манипуляции MSK минимизируется ширина основного лепестка спектра радиосигнала. Для снижения ширины основного лепестка и уменьшении боковых лепестков предложена частотная манипуляция GMSK с минимальным сдвигом и низкочастотным фильтром, сглаживающим импульсы видеосигнала. Фильтрация осуществляется фильтром Гаусса, амплитудно-частотная характеристика которого описывается выражением
K(f)
= exp[-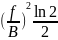 ],
],
где B – полоса пропускания фильтра Гаусса.
Параметр
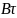 определяет
уровень боковых лепестков , его типичные
значения - десятые доли единицы. При
уменьшении параметра
боковые лепестки спектра радиосигнала
становятся меньше,
однако его малые значения существенно
сглаживают импульсы видеосигнала, что
увеличивает ошибки при отделении
логической 1 от логического 0 в приемнике.
определяет
уровень боковых лепестков , его типичные
значения - десятые доли единицы. При
уменьшении параметра
боковые лепестки спектра радиосигнала
становятся меньше,
однако его малые значения существенно
сглаживают импульсы видеосигнала, что
увеличивает ошибки при отделении
логической 1 от логического 0 в приемнике.
Модуляйия цифровым сигналом
