Скляр в пересказе Орешкина

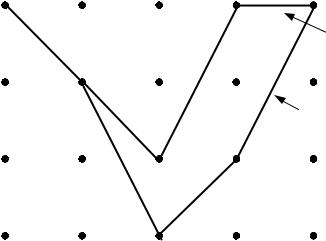
шую метрику; такой путь называется выживающим. Отбор выживающих путей выполня-

ется для каждого состояния. Таким образом, декодер углубляется в решетку, принимая решения путем исключения менее вероятных путей. Предварительный отказ от маловеро-

ятных путей упрощает процесс декодирования. Отметим, что задачу отбора оптимальных путей можно выразить как выбор кодового слова с максимальной метрикой правдопо-

добия или минимальной метрикой расстояния.

На рис.7.10 представлен пример декодирования Витерби, передаваемая последова-

тельность U и принимаемая последовательность Z. Если выбирать из двух вариантов пу-

тей, сошедшихся в одной точке, более коротким и, следовательно, более правдоподобным является путь с меньшей метрикой. В точке t5 придется рассмотреть по паре путей в каж-

дой из четырех возможных точек, выбрать наиболее короткий путь для каждой пары, по-

сле чего останутся ("выживут") только четыре пути из восьми, на следующем шаге опера-

ция выбора повторяется.

c = 01

01(0)

01(0)

d = 11

Рис.7.10. Декодирование Витерби

101

Примеры задач

Пример 7.1. Нужно создать код обнаружения ошибок (4,3) положительной чет-

ности, причем символ четности должен располагаться на крайней левой позиции кодового слова. Какие ошибки может обнаружить код? Вычислите вероятность необнаруженной ошибки сообщения, предполагая, что все символьные ошибки являются независимыми событиями и вероятность ошибки в канальном символе равна р = 10–3.

Решение.

Код может выявлять все комбинации с одной или тремя ошибками. Вероятность необнаруженной ошибки равна вероятности появления где-либо в кодовом слове двух или четырех ошибок.

Всего восемь различных сообщений с положительной четностью.

Пример 7.2. Сравните вероятность ошибки в сообщении для двух каналов связи -

обычного и использующего кодирование с коррекцией ошибок. Пусть некодированная

ние кода с коррекцией ошибок (15,11), предоставляющего возможность исправления лю-

бых 1-битовых ошибочных комбинаций кода в блоке из 15 бит. Будем считать, что демо-

дулятор принимает жесткие решения и передает демодулированный код прямо на декодер, который, в свою очередь, определяет исходное сообщение.

102

Решение.

Пусть pu Q2Eb / N0 и pc Q2Ec / N0 - соответственно вероятности символьных

ошибок в канале без кодирования и с кодированием, где Eb / N0 - отношение энергии бита к спектральной плотности мощности шума, Ec / N0 - отношение энергии кодированного бита к спектральной плотности мощности шума.

Без кодирования:

Для Q(x) используется следующее приближение:

Вероятность того, что некодированный блок сообщений PMu будет принят с ошиб-

кой, равна 1 минус произведение вероятностей того, что каждый бит будет обнаружен правильно. Таким образом,

Вероятность ошибки, по крайней мере, в одном из 11 бит

С кодированием: допустим, рассматриваемая система - это система связи реального времени, где задержки недопустимы, а скорость передачи канальных символов, или ско-

рость передачи кодированных битов, равна Rc = 15/11 скорости некодированной передачи.

Rc 48001511 6545 [бит/с]

и

Для каждого кодового бита значение Eb / N0 меньше, чем в случае с некодирован-

ными битами данных. Это объясняется тем, что скорость передачи канальных битов воз-

росла, а мощность передатчика при этом не изменилась.

Сравнивая вероятности, можно видеть, что вследствие внесения избыточности ве-

роятность ошибки в канальном бите уменьшилась. За то же время и с теми же номиналь-

ными мощностями нужно обнаружить большее число битов; повышение производитель-

ности в результате кодирования еще не очевидно. Вычислим теперь частоту появления

ошибок в кодированном сообщении PMc .

Суммирование начинается с j = 2, поскольку код позволяет исправлять все 1-

битовые ошибки в блоках из n = 15 бит. Достаточно хорошее приближение можно полу-

чить, используя только первый член суммы.

Сравнивая результативные выражения, можно видеть, что вследствие применения кода с коррекцией ошибок вероятность ошибки сообщения была уменьшена примерно в

58 раз.

Пример 7.3. С помощью полиномиального генератора g( X ) 1 X X 3 получите систематическое кодовое слово из набора кодовых слов (7, 4) для вектора сообщения m = 1101.

Решение.

Итак,

n 7, k 4, n k 3.

Информационное слово 1101 представим в виде полинома m(X ) 1 X 2 X 3 .

Подвинем разряды нашего сообщения влево.

Нам нужно из 1101 сделать 1101000, т.е. дописать справа три нуля, для этого мы

умножаем наш полином сообщения на X n k

X n k m( X ) X 3 (1 X 2 X 3 ) X 3 X 5 X 6 .

Любое кодовое слово должно без остатка делиться на полином генератора. Разде-

лив X n k m( X ) на g(X), можно записать следующее:

Значит, нашему слову X n k m( X ) для того чтобы быть кодовым, не хватает рассчи-

танного остатка. Прибавим этот остаток и получим результативное кодовое слово

U( X ) p(X ) X 3m(X ) 1 X 3 X 5 X 6 ;

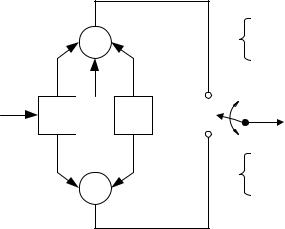
Пример 7.4. Закодировать сообщение m = 101, используя кодер на рис.7.11.

Рис.7.11. Сверточный кодер (степень кодирования 1/2, K = 3)

Решение.

У кодера есть начальное состояние, допустим, 0, т.е. во всех разрядах сдвигового регистра до начала кодирования находится нуль.

В первый такт на вход кодера поступает первый бит 1, и внутри кодера появляется

100.Суммируя разряды в соответствии со связями сумматоров, получим: u1 = 1, u2 = 1.

Во второй такт на вход кодера поступает 0; все, что было внутри, сдвигается и по-

лучаем в разрядах сдвигового регистра 010. Суммируем, получаем: u1 = 1, u2 = 0.

В третий такт на вход кодера поступает 1; все, что было внутри, сдвигается и полу-

чаем в разрядах сдвигового регистра 101. Суммируем, получаем: u1 = 0, u2 = 0.

На выходе мы получим U = 11.10.00.

Пример 7.5. Оценить возможности блочного кода (10,5) к исправлению ошибок.

Решение.

Воспользуемся пределом Хэмминга: n – k = 5, отсюда

довательно, код может исправить не более двух ошибок.

105

Пример 7.6. Выяснить, является ли полином g( X ) X 3 X 1 генератором для

циклического кода (7,5).

Решение.

Представленный полином может являться генератором для кода (7,5).

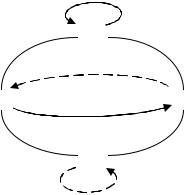
Пример 7.7. Связи для трехразрядного сверточного кодера заданы как g1 010 и g2 101. Изобразите диаграмму состояний для такого кодера.

Решение.

Для данного кодера диаграмма состояний имеет вид:

Примем за начальное состояние нули во всех разрядах сдвигового регистра. В слу-

чае прихода нуля в регистре сдвига будет три нуля и на выходе сумматоров будут нули. В

случае прихода единицы в сдвиговом регистре будет 100 и согласно связям сумматоров на выходе будет 01. Изобразим это на диаграмме состояний, в состоянии кодер может при-

нять либо нуль (сплошная линия), либо единицу (пунктирная линия), что переведет кодер либо в состояние 00, либо в состояние 10. "По пути" кодер сформирует на выходе сумма-

торов соответствующий кодовый символ. Эта процедура аналогична для всех возможных состояний.

106

Контрольные вопросы

1.Для чего применяется канальное кодирование?

2.На каком принципе основано канальное кодирование?

3.Перечислите известные вам методы канального кодирования.

4.Что такое матрица Адамара?

5.Что такое расстояние Хэмминга?

6.В чем заключается разница между блочными и неблочными кодами?

7.В чем состоит ключевая разница между диаграммой состояний и древовидной диаграммой?

8.На каком принципе основан алгоритм Витерби?

107

Литература

1. Скляр Б. Цифровая связь. Теоретические основы и практическое применение:

пер. с англ. - 2-е изд., испр. - М.: Вильямс, 2007. - 1104 с.

2. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: Высшая школа, 2005. -

464 с.

3.Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Дрофа, 2006. - 720 с.

4.Корниенко А.И. Теоретические основы передачи и обработки сигналов. - М.:

МИЭТ, 1996. - 227 с.

5. Сергиенко А.Б. Цифровая обработка сигналов: учеб. пособие. -

3-е изд. - М.: БХВ-Петербург, 2011. - 768 с.

6. Прокис Дж. Цифровая связь. - М.: Радио и связь, 2000. - 800 с.

108