
- •Проектирование антенно-фидерных устройств
- •Введение
- •Список употребляемых сокращений
- •Семинар № 1. Расчет основных параметров МПЛ
- •Семинар № 4. Проектирование делителей мощности
- •Семинар № 8. Рупорные антенны
- •Семинар № 9. Расчет линзовых антенн
- •Семинар № 10. Расчет антенн поверхностных волн
- •Семинар № 13. Проектирование передающих АФАР
- •Семинар № 17. Адаптивные антенные решетки
- •Содержание
Семинар № 10. Расчет антенн поверхностных волн
К антеннам поверхностных волн следует в первую очередь отнести спиральные и диэлектрические антенны.
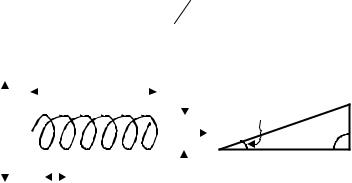
Спиральная антенна представляет собой отрезок спирали из металлической проволоки либо ленты, вдоль которого распространяется замедленная (или поверхностная) бегущая волна (рис.1). Спираль с шагом S и диаметром D имеет длину витка L и угол намотки α . Общая
длина спирали l = nS , где n - число витков. Возбуждающее устройство состоит из экрана диаметром Dэ ≥ λ2 и питающего фидера. Экран
препятствует затеканию тока на внешнюю поверхность коаксиального фидера и выполняет роль рефлектора, ослабляющего излучение в заднюю полусферу.
|
|
|
|
|
|
|
|
|
l = nS |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
э |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
L |
|||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
z |
πD |
|||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис.1. Цилиндрическая спиральная |
|
|||||||||
|
|
|
|
|
|
|
|
|
антенна (а) и развертка ее витка (б) |
|
|||||||||
Вдоль витка проволоки распространяется бегущая волна тока с коэффициентом замедления pi , а вдоль оси системы - замедленная бегущая волна с коэффициентом замедления p. Легко видеть, что p = pi  sin α .
sin α .
Направленные свойства спирали зависят от соотношения ее размеров и длины волны. С практической точки зрения представляет интерес режим осевого излучения, когда L λ. В этом случае вдоль
оси спирали распространяется волна Ti , а вдоль провода спирали возникает бегущая волна тока, коэффициент замедления которой в
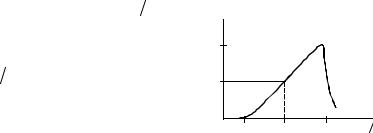
диапазоне |
длин волн |
0,7 < λ L <1,3 |
pi |
|
|
|
||||
изменяется линейно, как показано на |
|
|
|
|||||||
|
|
|
|
|||||||
рис.2, т.е. в |
этом |
диапазоне |
1,6 |
|
|
|
||||
частот |
|
длина |
волны |
тока |
|
|
|
|
||
Λi = λ pi |
= const . |
|
|
Максимум |
1,3 |
|
|
|
||
диаграммы |
направленности |
антенны |
|
|
|
|||||
ориентирован вдоль оси z, а поле имеет |
1 |
|
|
|
||||||
эллиптическую поляризацию [1]. |
0,7 |
1 |
1,3 |
λ L |
||||||
Как показывают расчеты, один |
Рис.2. Частотная зависимость |
|||||||||
виток |
спирали |
обладает |
слабой |
|||||||
направленностью. |
|
|
Обострение |
коэффициента замедления волны |
||||||
диаграммы |
|
|
обеспечивается |
тока в проводе спирали |
||||||
совокупностью витков, т.е. спиральную |
|
|
|
|
||||||
антенну можно представить как линейную систему с осевым |
||||||||||
излучением. Число витков выбирается в переделах |
3 < n <12 . При |
|||||||||
n < 3 |
поле в антенне |
не |
успевает сформироваться, |
а при |
n >12 |
|||||
последующие витки уже не вносят вклад в излучение, поскольку ток в |
||||||||||
них исчезающе мал. |
|
|
|
|
|
|
|
|
||
Существуют два режима осевого излучения: режим круговой |
||||||||||
поляризации и режим максимального КНД. |
|
|
|
|||||||
Рассмотрим режим круговой поляризации. |
|
|
|
|||||||
Сложение полей отдельных витков в дальней зоне вдоль оси имеет |
||||||||||
место при условии, что ток в каждом последующем витке отстает по |
||||||||||
фазе от тока в предыдущем витке на угол φ, определяемый выражением |
||||||||||
|
|
|
|
φ − kS = 2π. |
|
|
|
(1) |
||
В формуле (1) учтено, что поле от предыдущего витка на пути к |
||||||||||
последующему витку приобретает фазовый набег |
kS . С |
другой |
||||||||
стороны, волна тока приобретает на одном витке фазовый набег |
|
|||||||||
φ = kpi L . |
|
(2) |
Подставляя (2) в (1), находим |
|
|
kpL = kS + 2π |
или pL = S + λ . |
(3) |
Из формулы (3) легко получить угол намотки спирали, соответствующий режиму круговой поляризации:
|
pi = |
S + λ |
= |
S |
+ |
λ |
= sin α + |
λ . |
(4) |
||
|
L |
L |
L |
||||||||
|
λ |
|
|
|
|
|
L |
|
|||
Как правило, при |
=1 pi |
1,3 , |
при этом |
sin α =1,3 −1 = 0,3 , а |
|||||||
|
L |
|
|
|
|
|
|
|
|
|
|
α=17o .
Врежиме максимального КНД (оптимальный режим) необходимо, чтобы первый и последний витки спирали излучали в противофазе, т.е. чтобы обеспечивалось равенство
φn − nkS = 2πn + π. |
(5) |
|||||
Учитывая, что фазовый сдвиг последнего витка определяется как |
|
|||||
φn = kpi оптL , |
(6) |
|||||
из формул (5) и (6) легко получить |
λ |
|
|
|||
|
S + λ + |
|
||||
pi опт = |
2n |
. |
(7) |
|||
|
||||||
L |
|
|||||
|
|
|
|
|
||
Формула (7) позволяет определить оптимальный угол намотки спирали:
|
p |
− λ |
|||
sin αопт = |
iопт |
|
L |
, откуда αопт 12o . |
|
|
|
|
|||
1 + |
λ |
|
|||
2l |
|||||
|
|
||||
В режиме максимального КНД поле оси антенны поляризовано эллиптически, но близко к кругу ( χ > 0,5 ).
ДН спиральной антенны рассчитывается по формуле для линейной системы с осевым излучением
F(θ)= fв(θ)f (θ), (8)
где fв (θ) - ДН одного витка;
|
sin |
nk |
(pL − S cos θ) |
|
|||
|
|
|
|
|
|||
|
|
2 |
|
|
|||
f (θ)= |
|
|
|
- |
|||
|
|
|
k |
|
|||
|
|
|
|
|
|||
|
n sin |
|
|
(pL − S cos θ) |
|
||
|
|
||||||
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
множитель направленности системы; p = pi  sin α - коэффициент
sin α - коэффициент
замедления волны вдоль оси спирали.
Из формулы (8) следуют соотношения для расчета электрических параметров спиральной антенны (при α =12 ÷17o ):
∆θ0,5 |
52 |
λ |
λ |
; |
D0 =15 |
l |
|
L |
2 |
Zвх |
=140 |
L |
, [Ом]. |
(9) |
|
L |
l |
λ |
|
|
; |
λ |
|||||||||
|
|
|
|
|
λ |
|
|
|
0,7 < λ <1,3L . |
||||||
Рабочий диапазон определяется из условия |
|
||||||||||||||
Диаметр экрана выбирается в пределах (1,0 ÷ 1,6)l. |
|
|
|
|
|||||||||||
Достоинствами |
|
|
спиральных |
|
антенн |
являются |
простота |
||||||||
конструкции, |
широкая |
полоса |
рабочих |
частот ( λmax λmin =1,7 ), |
|||||||||||
недостатком |
- невозможность |
получения для |
одиночной |
спирали |
|||||||||||
ширины ДН меньше 25o . Для обострения ДН применяют решетку из |
||||||||
спиралей. |
Для |
получения |
сверхшироких |
рабочих |
полос |
частот |
||
( λmax λmin > 3 ) |
применяют |
конические |
спиральные |
антенны. |
||||
Широкополосность достигается за счет того, что работает та часть |
||||||||
конической спирали, где выполняется условие λ L . |
|
|
|
|||||
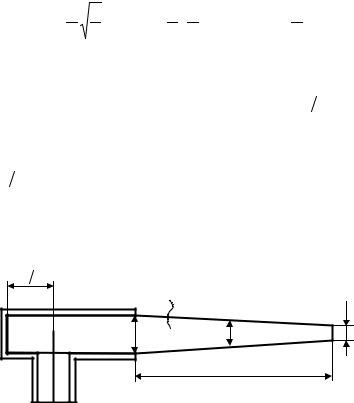
Диэлектрическая антенна представляет собой диэлектрический |
||||||||
стержень, выходящий из круглого волновода. Конструкция антенны |
||||||||
показана на рис.3. |
|
|
|
|
|
|
|
|
Λ 4 |
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
max |
|
ср |
|
|
d |
|
|
|
|
|
|
|
|
||
|
|
|
d |
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
Рис.3. Конструкция стержневой диэлектрической антенны
Принцип работы антенны состоит в том, что вдоль стержня распространяется волна HE11 (основной тип), фазовая скорость которой
зависит от ε , d, λ . Волна HE11 вызывает поляризацию диэлектрика.
При этом поляризационные токи могут рассматриваться как элементарные излучатели, сдвинутые относительно друг друга по фазе,

как в бегущей волне. Поле излучения всей антенны равно сумме полей излучения элементарных излучателей (как в линейной системе):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(θ)= f1(θ)f (θ), |
|
|
|
(10) |
||||||||
|
|
|
|
|
|
sin |
kL |
|
(p −cos θ) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где |
f (θ)= |
|
|
2 |
|
- множитель направленности; L - длина |
|||||||||||||||||||||
|
|
kL |
(p −cos θ) |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
f1(θ) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
стержня; p - коэффициент замедления волны в стержне; |
- ДН |
||||||||||||||||||||||||||
элементарного излучателя. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Зависимость 1 p от d λ для различных ε представлена на рис.4. |
||||||||||||||||||||||||||
Для |
|
уменьшения отражения |
от конца антенны |
стержень |
делают |
||||||||||||||||||||||
1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коническим, |
при |
|
|
этом |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε=2 |
|
|
|
|
dmax = λ |
π(ε −1), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0,8 |
|
|
|
|
|
3 |
|
|
|
dmin = 0,63dmax . |
|
|
|
|
|||||||||||||
0,6 |
|
|
|
|
|
|
|
|
Порядок |
|
|
расчета |
|||||||||||||||
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||
0,4 |
|
|
|
|
|
|
|
|
диэлектрической |
|
|
антенны |
|||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
||||||||||||||||||
0,2 |
|
|
|
|
|
|
|
следующий: |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
30 |
|
|
|
|
|
λ , |
||||||||||||||||
|
|
|
|
|
|
|
|
1) |
задаются |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε ; |
|
|
|
|
|
|
0 |
0,2 |
0,4 0,6 0,8 1,0 |
d λ |
|
|
|
|
|
|||||||||||||||||||
2) |
определяются |
||||||||||||||||||||||||||
|
|
|
Рис.4. Частотная |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
dmin и dmax ; |
|
|
|
|
|
||||||||||||||||
зависимость коэффициента |
|
|
3) |
по |
|
графику |
|||||||||||||||||||||
|
|
|
замедления волны |
|
|
|
рис.4 находятся pmin |
и |
pmax ; |
||||||||||||||||||
|
|
|
|
|
|
в стержне |
|
|
|
4) |
определяется |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pопт = (pmax + pmin ) |
2 ; |
|
|
|||
5)используя pопт , определяющий оптимальную
длину стержня, при которой обеспечивается максимум КНД, определяют
Lопт = |
λ |
|
2(pопт −1); |
(11) |

6) определяют электрические параметры антенны из условий
|
∆θo0,5 60o |
λ |
; |
D0 = (7 ÷8) |
L |
. |
(12) |
|
|
|
|||||
|
|
L |
|
λ |
|
||
Пример 1. Цилиндрическая спиральная антенна с углом намотки |
|||||||
α =14o |
предназначена для работы |
в диапазоне λ =10 ÷15 |
см. |
||||
Определить диаметр витков D, при котором в спирали обеспечивается |
|||||||
режим осевого излучения. |
|
|
|
|
|||
Решение. 1. Находим λср = (15 +10) 2 =12,5 см. |
|
||||||
2. В режиме осевого излучения L = λср =12,5 см. |
|
||||||
3. |
Из развертки спирали (рис.1,б) имеем cos α = πD L , откуда |
||||||
D = Lπ cos α = 3,8 см.
Пример 2. Определить геометрические размеры цилиндрической спиральной антенны, обеспечивающей в режиме круговой поляризации
D0 =15 на длине волны λ =15 см. |
|
|
|
|
|||||||||||||||
Решение. 1. Задаемся pi |
=1,3 (в соответствии с рис.2). |
|
|||||||||||||||||
2. |
Полагаем L = λ =15 см. |
|
|
|
|
|
|
|
|
||||||||||
3. |
По формуле (3) находим S = pi L − λ =1,3 15 −15 = 4,5 см. |
||||||||||||||||||
4. |
Из развертки спирали находим |
|
|
|
|
||||||||||||||
|
|
|
D = |
|
L |
cos α = |
|
15 |
cos17o = 4,6 см. |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|||
5. |
По формуле (9) определяем |
|
|
|
|
||||||||||||||
|
l = nS = |
|
D |
0 |
λ |
|
λ 2 |
= |
15 15 |
=15 см, откуда |
n 3 . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
15 |
|
|
|
15 |
|
|
|
||||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|||||||
Пример 3. |
|
|
Рассчитать |
|
|
|
относительную |
длину |
L λ |
||||||||||
диэлектрической |
антенны |
из |
|
полистирола ( ε = 2,6 ) диаметром |
|||||||||||||||
d = 0,5λ и определить ее параметры излучения. |
|
|
|||||||||||||||||
Решение. 1. По графику |
|
рис.4 находим 1 p = 0,7 , |
откуда |
||||||||||||||||
pопт =1,43 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
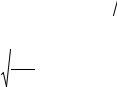
2. |
По формуле (11) определяем L λ = |
|
1 |
=1,16 . |
|||||
2(p −1) |
|||||||||
3. |
По формулам (12) получаем |
|
|
|
|
|
|
||
|
∆θo0,5 60o |
|
|
|
|
L |
= 7,5 ×1,16 =8,7. |
||
|
1 |
= 55,7o; |
D0 |
= 7,5 |
|||||
|
|
|
|||||||
|
1,16 |
|
|
|
|
λ |
|||
Задание 1. Определить геометрические размеры и параметры излучения цилиндрической спирали, обеспечивающей в оптимальном
режиме D0 = 20 на длине волны λ =10 см.
Задание 2. Рассчитать оптимальную коническую диэлектрическую антенну из полистирола ( ε = 2,6 ), работающую на длине волны
λ = 7 см.
Литература
1. Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. - М.: Сов. радио, 1974. - С. 309 - 328; 393 - 399.
Семинар № 11. Проектирование линейной ФАР
сзаданным уровнем боковых лепестков
Сцелью уменьшения УБЛ в ФАР применяется неравномерное амплитудное возбуждение типа “косинус на пьедестале”:
I (z)=1 + ∆cos(2πz L), |
|
z |
|
≤ L 2 , |
(1) |
|
|
||||
где I (z) - амплитудное возбуждение |
|
вдоль антенны; z - |
текущая |
||
координата; ∆ - параметр, определяющий относительное уменьшение возбуждения на краю антенны; L - геометрическая длина антенны.
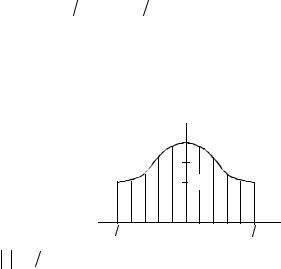
Распределение для данной зависимости I (z) показано на рис.1.
Раскладывая косинус |
в сумму |
I (z) |
|
|
|
|
двух |
экспонент, |
приведем |
1 + ∆ |
|
|
|
амплитудное распределение к сумме |
|
1 |
|
|
||
трех равномерных распределений с |
|
|
|
|||
линейно |
меняющимися |
фазовыми |
|
1 − ∆ |
|
|
сдвигами, являющихся членами ряда |
|
|
|
|
||
Фурье: |
|
|
|
|
|
|
|
|
L 2 |
|
0 |
L 2 |
z |
1 |
|
|
I (z)= ∑an e jnξkz , |
z ≤ L 2 , |
|
n=−1 |
Рис.1. Амплитудное рас- |
|
пределение ФАР типа |
||
|
||
|
“косинус на пьедестале” |
|
где коэффициенты |
равны a0 =1, |
a1 = a−1 = ∆ 2 , а коэффициенты замедления ξ = λ
2 , а коэффициенты замедления ξ = λ L .
L .
Множитель направленности, соответствующий распределению (1), определяется суммой:
1 |
sin(φ0 − nπ) |
|
|
||||
F(θ)= ∑ an |
, |
(2) |
|||||
φ |
0 |
− nπ |
|
||||
n=−1 |
|
|
|
|
|
||
где φ0 = 0,5kL cos θ.
Метод, с помощью которого был получен множитель |
||||||||
направленности (2), в теории антенн называется методом парциальных |
||||||||
ДН. Согласно этому методу каждому члену ряда, представляющего |
||||||||
амплитудно-фазовое распределение антенны, соответствует своя |
||||||||
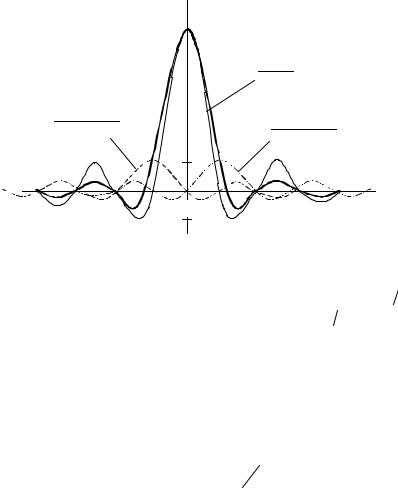
парциальная ДН. Суммирование трех парциальных ДН, входящих в (2), |
||||||||
показано на рис.2 для случая ∆ = 0,4 . |
|
|
|
|
|
|||
|
|
|
F (θ) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
sin φ0 |
|
|
|
|
|
|
|
|
φ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin φ |
0 |
+ π |
φ |
|
− π |
|||
|
|
|
sin |
0 |
|
|||
φ0 + π |
|
|
|
|
|
|||
|
φ |
0 |
− π |
|
||||
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2π |
−π 0 π |
2π |
|
|
|
φ0 |
|
|
|
|
−0,2 |
|
|
|
|
|
Рис.2. Снижение УБЛ при спадающем амплитудном |
|
|||||||
|
|
|
распределении |
|
|
|
|
|
Из рис.2 видно, что добавление к основной ДН вида (sin φ0 ) φ0 |
||||||||
двух сдвинутых на ± π поправочных ДН с амплитудой ∆ 2 приводит к |
||||||||
резкому уменьшению УБЛ, сопровождающемуся некоторым |
||||||||
расширением главного лепестка. |
|
|
|
|
|
|||
Изменяя значение ∆ , можно |
снизить уровень |
наибольшего |
||||||
бокового лепестка (в дБ) до значений |
|
|
|
|
|
|||
t ≈ −(13 +13∆ + 22∆2 ). |
(3) |
При этом ширина луча по половинной мощности
∆θ0,5 ≈ (1 + 0,636∆2 ) 51o λ |
L |
, |
(4) |
|
|
|
где множитель в скобках представляет собой так называемый коэффициент расширения луча.
Расширение главного лепестка приводит к снижению КНД с нижней оценкой
D = |
|
D0 |
, |
|
2 |
||
1 |
+ 0,5∆ |
|
|
где D0 - КНД антенны с равномерным амплитудным распределением.
Одной из ключевых задач при проектировании линейных (плоских) антенных решеток является грамотный (оптимальный) выбор межэлементного расстояния. Этим объясняется стремление разработчика максимально “растянуть” межэлементное расстояние, что однозначно минимизирует количество каналов (излучателей) и удешевляет проектируемую систему. Препятствием этому является возможность появления побочного дифракционного максимума в секторе обзора (сканирования).
При применении ненаправленных (изотропных) излучателей формула для расчета межэлементного расстояния имеет следующий вид:
dmax ≤ |
|
|
λ |
, |
|
|
|
|
|||
1 |
+ sin θск |
||||
|
|
||||
где θск - предельный угол сканирования антенной решетки (угол θ
отсчитывается от нормали к плоскости решетки); λ - длина волны. Эта формула предполагает, что для выбранного межэлементного
расстояния дифракционный максимум вообще не появится в “видимой” области.
Однако в случае применения направленных излучателей, что обычно имеет место на практике, формула для межэлементного расстояния трансформируется в следующую:
dmax ≤ |
λ |
, |
(5) |
|
|
||||
sin θд + sin θск |
||||
|
|
|
где θд - направление дифракционного максимума.
Применение этой формулы обусловлено теоремой перемножения в теории антенн, в соответствии с которой полная ДН антенной решетки есть произведение ДН одного элемента на множитель направленности решетки. В связи с этим становится справедливым следующее
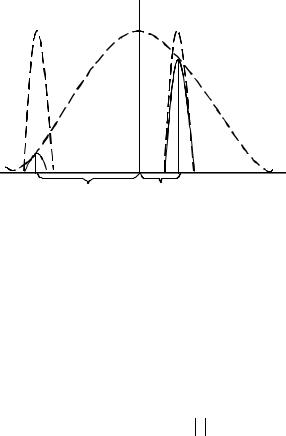
утверждение: если один элемент имеет незначительное излучение в направлении побочного максимума решетки, то последний окажется подавленным, как показано на рис.3.
|
F(θ,ϕ) |
|
1 |
θд |
θ |
θск |
|
Рис.3. Влияние ДН элементов ФАР на уровень основного |
|
луча и дифракционного максимума |
|
Формула (5) имеет очень важное значение при проектировании антенных решеток с малым сектором сканирования ( θск ≤ 30o ÷ 40o ).
Пример 1. Выбрать вид амплитудно-фазового распределения для линейной антенной решетки с заданным уровнем максимального бокового излучения t ≤ −20 ; 25; 30 дБ. Для каждого случая оценить коэффициент в формуле определения ширины луча по половинной мощности и коэффициент уменьшения КНД.
Решение. 1. Для решения поставленной задачи воспользуемся распределением (1) типа “косинус на пьедестале”
I (z)=1 + ∆cos(2πz L), z ≤ L
L), z ≤ L 2 .
2 .
Значение ∆ (уменьшение амплитуды возбуждения на краю антенны) определяем из выражения (3):
t ≈ −(13 +13∆ + 22∆2 ),

т. е.
22∆2 +13∆ +13 = 20; 25; 30 .
Решая квадратное уравнение для каждого случая, находим
∆1 = 0,34; ∆2 = 0,5; ∆3 =0,63 .
Соответствующие распределения имеют следующий вид:
I1 (z)=1 + 0,34 cos(2πz L); I2 (z)=1 + 0,5 cos(2πz L);
I3 (z)=1 + 0,63cos(2πz L).
L).
2.Для равноамплитудного распределения формула, определяющая ширину главного лепестка, имеет следующий вид:
|
Aλ |
|
o |
∆θ = |
|
, |
где A ≈ 51 . |
L |
Для определения коэффициента A в каждом случае воспользуемся формулой (4). Коэффициент A определяется как
|
A ≈ (1 + 0,636∆2 ) 51o . |
|
Отсюда A ≈ 54,7o; |
A ≈ 59o; |
A ≈ 63,8o . |
1 |
2 |
3 |
3. Значение КНД может быть записано в виде
D = βD0 ,
где β ≈1 (1 + 0,5∆2 ). Тогда β1 ≈ 0,945; β2 ≈ 0,89; β3 ≈ 0,84 .
(1 + 0,5∆2 ). Тогда β1 ≈ 0,945; β2 ≈ 0,89; β3 ≈ 0,84 .
Для других типов амплитудных распределений (например, “парабола на пьедестале”, “линейное спадающее к краям” и т.д.)
значения ∆i , Ai , βi можно взять из таблиц, которые имеются в
соответствующих справочниках по антенной технике.
Пример 2. Спроектировать антенную решетку с сектором сканирования ∆θск = ±30o с максимальным уровнем боковых лепестков t ≤ −22 дБ. Определить значения ∆ , A , β и dmax . Считать,
что ДН излучателя подчиняется закону f (θ)= cosα(θ).

Решение. 1. При проектировании АР предполагается, что ее усиление меняется в секторе сканирования на величину порядка –3 дБ, т.е. обычно падение усиления на краю сектора сканирования составляет эту величину. Учитывая, что усиление пропорционально квадрату амплитуды, а также то, что падение усиления всей АР на краю сектора сканирования определяется ДН излучателя, можно записать
f 2 (θ)= 0,5 , т.е. cos2α (30o )= 0,5 .
Отсюда находим значение α :
α= 1 (lg 0,5 )≈ 2,5; f (θ)= cos2,5 (θ). 2 lg cos 30°
2.Воспользуемся формулой (5) для определения dmax :
dmax ≤ |
λ |
. |
|
|
|||
sin θд + sin θск |
|||
|
|
При определения θд вспомним, что при этом значении угла
возникший дифракционный максимум должен “подавляться” ДН элемента до заданного уровня t ≈ −22 дБ, что составляет по мощности величину порядка 0,006. Тогда можем записать
cos5 (θд )= 0,006; θд = arccos(5 0,006 )≈ 69o .
Окончательно вычислим значение dmax :
dmax ≤ |
λ |
≈ 0,7λ . |
|
|
|||
sin 69o + sin 30o |
|||
3. Значения ∆ , A , |
|
||
β найдем по методике, приведенной в |
|||
предыдущем примере:
∆ ≈ 0,41; A ≈ 56,4o; β ≈ 0,92 .
Допустим, что проектируется плоская решетка. Усиление элемента может быть оценено по формуле

g0 = |
4πSэф |
= |
4πdmax2 σ |
, где |
σ ≈ 0,7 . |
|
λ2 |
λ2 |
|||||
|
|
|
|
Тогда
g0 = 4π(0,7λλ2)2 0,7 ≈ 4,3 ед.
Задание 1. Спроектировать антенную решетку с сектором
сканирования ∆θск |
= ±15o , |
с |
максимальным УБЛ t ≤ −18 дБ. |
Определить значения |
∆ , A , β |
и |
dmax . Считать, что ДН излучателя |
подчиняется закону f (θ)= cosα(θ).
Задание 2. Выбрать вид амплитудного распределения для линейной антенной решетки с заданным УБЛ t ≤ −17 ; − 35 дБ. Для каждого случая оценить коэффициент в формуле определения ширины луча по половинной мощности Ai и коэффициент уменьшения КНД βi .
Литература
1. Сазонов Д.М. Антенны и устройства СВЧ. - М.: Высшая школа, 1988. - С. 283 - 296; 292 - 298.
2. Чистюхин В.В. Антенно-фидерные устройства. - М.: МИЭТ, 1997. - С. 170 - 175.

Семинар № 12. Эффективность параболических зеркальных антенн
Эффективность параболических зеркальных антенн определяется в основном их коэффициентом направленного действия, который в свою очередь может быть определен формулой
D = |
4πS |
σ, |
(1) |
2 |
|||
|
λ |
|
|
где S - площадь возбуждаемой поверхности; λ - рабочая длина волны;
σ - суммарный коэффициент использования площади антенны. Суммарный КИП антенны определяется через произведение всех
коэффициентов, влияющих на эффективность работы ПЗА. Рассмотрим эти коэффициенты более подробно.
Апертурный коэффициент использования kа . Рассмотрим
раскрыв параболоида как излучающую поверхность. Во многих практических случаях распределение поля в раскрыве антенны может считаться синфазным и осесимметричным. Достаточно часто амплитуду поля можно аппроксимировать параболическим распределением с пьедесталом:
E(R)=1− ∆(R R )2 |
, |
(2) |
0 |
|
|
где R - текущий радиус-вектор от центра плоскости раскрыва антенны до любой точки плоскости раскрыва; R0 - радиус плоскости раскрыва;
∆ - уменьшение поля на краю раскрыва.
Для апертурного коэффициента использования антенны с параболическим распределением можно записать следующее выражение:
kа = |
1 |
− ∆ + 1 |
4 |
∆2 |
|
||
|
|
|
|
. |
(3) |
||
1 |
− ∆ + 1 |
3 |
∆2 |
||||
Коэффициент перехвата ko . |
|
|
|
||||
Обозначим |
полную мощность, |
||||||
излученную облучателем, через PΣ , а мощность, попадающую на зеркало антенны, через Pп . Тогда коэффициент

ko = Pп PΣ
характеризует эффективность канализации энергии облучателя на зеркало антенны и называется коэффициентом перехвата. Для хорошо
спроектированной ПЗА этот коэффициент имеет значение ko ≈ 0,95 .
Затенение раскрыва антенны. Пусть часть раскрыва антенны затенена какими-либо предметами (облучатель, питающая фидерная
линия, элементы крепления облучателя и т. д.). Обозначим через Sз затененную часть раскрыва антенны. Будем считать, что поле на незатененной части раскрыва S − Sз остается таким же, как если бы
затенения не существовало, а поле на затененной части было бы равно нулю. Такое предположение достаточно точно, если характерные размеры затенения поверхности превосходят λ .
Обозначим через kз коэффициент, характеризующий уменьшение
КНД антенны из-за затенения части ее раскрыва. Предполагая распределение поля в раскрыве антенны параболическим на пьедестале (см. формулу (2)), можно записать:
|
|
|
|
η2 |
|
2 |
|
k |
з |
= 1 |
− |
|
|
, |
(4) |
|
|||||||
|
|
|
1 − ∆ 2 |
|
|
|
|
|
|
|
|
|
|
|
где η = Rобл  R0 ; Rобл - характерный размер раскрыва облучателя.
R0 ; Rобл - характерный размер раскрыва облучателя.
Для оптимального облучения, когда поле на краю антенны составляет около 30% от поля в центре антенны, формула (4)
приобретает вид: |
|
kз = (1 −1.5η2 )2 . |
(5) |
Рассмотрим теперь эффект затенения, даваемый линией питания, расположенной в раскрыве антенны. Обозначив ширину линии через t,
можно записать (для t << R0 ):
|
|
t 1 − ∆ 3 |
2 |
|
|||
|
− |
|
(6) |
||||
|
|
|
|||||
kз = 1 |
πR0 1 − ∆ 2 |
. |
|||||
|
|
|
|
||||
Для случая оптимального возбуждения (1 − ∆ ≈ 0,3) имеем: |
|
||||||

|
|
t |
2 |
|
|
− 0,37 |
|
(7) |
|
kз = 1 |
R0 |
. |
||
|
|
|
|
Интерференция поля антенны и поля облучателя. При определении поля антенны в главном направлении обычно учитывается только излучение токов, текущих по поверхности параболоида. В ряде случаев, однако, необходимо учитывать также задний лепесток диаграммы облучателя. Интерференция этих двух полей приводит к изменению (увеличению или уменьшению) эффективности антенны.
Коэффициент kинт , учитывающий эту интерференцию, определяется
равенством |
|
kинт = [1 + Dобл D Fобл (π) e jφ ]2 , |
(8) |
где Dобл и D - коэффициенты направленного действия облучателя и антенны соответственно; Fобл (π) - уровень поля облучателя в заднем направлении; φ- угол сдвига фаз между полями антенны и облучателя.
Расчеты показывают, что для высоконаправленных антенн коэффициент kинт колеблется в зависимости от фазы φ в пределах
0,994 ÷ 1,006. Однако в случае сравнительно слабонаправленных параболических антенн, встречающихся часто в метровом и дециметровом диапазонах волн, где к тому же применяются вибраторные облучатели с невысоким защитным действием, учет
коэффициента kинт становится необходимым.
Фазовый фронт облучателя (точность установки облучателя по фокальной оси). В раскрыве антенны волна будет плоской, если фазовый фронт облучателя является точно сферическим и фазовый центр облучателя совмещен с фокусом параболоида. На практике, однако, фронт волны облучателя вблизи поверхности зеркала часто существенно отличается от сферического и, кроме того, возможна неточность в установке облучателя. Все это приводит к ухудшению эффективности антенны.
Если принять максимально допустимую величину искажения фазы в раскрыве равной π 8 , точность установки облучателя по фокальной оси определяется неравенством
8 , точность установки облучателя по фокальной оси определяется неравенством

∆f < |
λ |
|
32 sin 2 (φ0 2), |
(9) |
где φ0 - угол между фокальной осью и прямой, проведенной из фокуса
к кромке параболоида.
Из (9) видно, что необходимая точность установки облучателя уменьшается с ростом фокусного расстояния. В случае короткофокусных антенн необходимая точность установки облучателя
весьма высока. Так, при |
2φ0 =180o облучатель должен |
быть |
установлен с точностью |
± λ 16 . Поэтому целесообразно |
при |
разработке антенны обеспечить возможность перемещения облучателя вдоль оси, что дает возможность экспериментальным путем выбрать оптимальное место установки.
Точность обработки поверхности антенны. Отклонения формы поверхности зеркала от параболической приводят к нарушению синфазности поля в раскрыве антенны и ухудшают ее эффективность. Требования к точности выполнения поверхности зеркала можно получить, исходя из необходимой точности обеспечения синфазности поля в раскрыве. Обычно считают достаточным обеспечить
синфазность возбуждения раскрыва с точностью ± π 8 . При этом
8 . При этом
потери коэффициента усиления антенны не превосходят нескольких процентов.
Если распределение фазы в раскрыве антенны можно считать случайной величиной, то потери коэффициента усиления антенны определяются формулой
~2
kнт = e−φ ,
~
где φ - среднеквадратическое отклонение фазы в раскрыве от ее
среднего значения.
Для длиннофокусных антенн, когда можно считать, что cos(φ0  2)≈1, получаем:
2)≈1, получаем:
~ |
2 |
~ |
2 |
|
kнт = e−(4πδn λ) |
|
= e−158(δn λ) |
, |
(10) |

~
где δn - среднеквадратическое отклонение поверхности от расчетной.
Фазу поля в раскрыве (или распределение отклонений зеркала) при анализе обычно считают распределенной по нормальному закону.
Поэтому допуск на точность изготовления поверхности зеркала δдоп
связан со среднеквадратическим |
отклонением |
соотношением |
||||||||
~ |
|
|
|
|
ϕ |
|
< π 8 получаем: |
|
||
δдоп = 2,6δ . При этом из условия |
|
|
||||||||
|
δn |
|
< |
|
λ |
|
. |
(11) |
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||
|
|
32 cos(φ0 |
2) |
|||||||
|
|
|
|
|
|
|||||
Эффективность параболической антенны. В реальных условиях при расчете коэффициента направленного действия антенны необходимо учитывать не только распределение поля в раскрыве антенны и утечку энергии облучателя за края зеркала, но и ряд других факторов, влияющих на эффективность антенны. Если коэффициенты
kз , kинт , ko , kнт мало отличаются от единицы, коэффициент использования поверхности антенны может быть определен по формуле
σ = kаko kзkинтkнт . |
(12) |
В силу рассмотренных причин |
полный коэффициент |
использования параболической антенны с обычным, например, рупорным облучателем на практике не превосходит 0,5 ÷ 0,6. Коэффициент использования может быть увеличен до 0,65 ÷ 0,7 и более путем применения специальных облучателей с ДН, близкой к столообразной.
Пример. Спроектировать параболическую зеркальную антенну с коэффициентом усиления G = 40 дБ на частоте f =10 ГГц с уровнем
боковых лепестков, не превышающих –22 дБ. Считать распределение поля по раскрыву параболическим. Величина фокуса параболы равна
его радиусу ( F = R0 ).
Решение. 1. Оценим размер раскрыва параболы, исходя из того, что G ≈ D и ориентировочно суммарный КИП σ = 0,7 (см. формулу
(1)):
G = D =10000 ед. G = 4λπ2S σ,
отсюда
S= λ2 G ≈10200 см2 ,
4π σ
тогда R0 ≈ 57 см.
2. Используя формулу для параболического распределения поля по раскрыву E(R)=1− ∆(R R0 )2 из табл. 5.1, [1, с.113] найдем значение
R0 )2 из табл. 5.1, [1, с.113] найдем значение
∆≈ 0,65 .
3.Параболическая антенна - длиннофокусная, тогда
(φ0 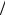 2)= R0
2)= R0  2F = 0,5 ,
2F = 0,5 ,
отсюда φ0 ≈ 53o .
4.По формуле (3) рассчитаем апертурный КИП антенны:
1− 0,66 + 0,435 4
=0,435 ≈ 0,92 .1 − 0,66 +
3
5.Значение коэффициента перехвата ko примем равным 0,95.
6.При заданном УБЛ примем Rобл ≈ 2λ , тогда
η= Rобл  R0 ≈ 0,15; kз′ = (1 −1,5η2 )2 ≈ 0,93 .
R0 ≈ 0,15; kз′ = (1 −1,5η2 )2 ≈ 0,93 .
Предположим, что имеется волновод, питающий облучатель, шириной
t = λ и три тяги шириной t = λ 2 :
2 :
kз′′ = (1 − 0,37 λ R0 )2 ≈ 0,945; kз′′′= (1 − 0,37 λ
R0 )2 ≈ 0,945; kз′′′= (1 − 0,37 λ 2R0 )2 ≈ 0,97;
2R0 )2 ≈ 0,97;
k&з = kз′kз′′(kз′′′)3 ≈ 0,8.
Здесь использованы формулы (4) - (7).
7. Для вычисления kинт по формуле (8) потребуем, чтобы уровень заднего облучения не превышал значения Fобл (π)≤ −20 дБ. Тогда
kинт = 1 ± 0,01 18 104 2 = 10,,00089992 ≈1.
8. Прежде чем рассчитывать коэффициент kнт , оценим необходимую точность выполнения нашей параболы по формуле (11):
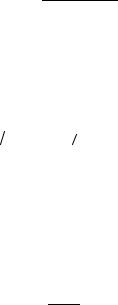
δn < 32 cosλ(φ0  2).
2).
Из формулы видно, что вблизи центра параболоида ( φ = 0 ) необходимая точность выполнения зеркала максимальна:
δn ≈ ±λ 32 ≈ ±0,093 мм.
32 ≈ ±0,093 мм.
На краю параболы δn ≈ ±1,05 |
мм. С |
учетом этих значений и |
|
~ |
, используя формулу (10), получим: |
||
соотношения δn ≈ 2,6δn |
|||
~ |
2 |
2 |
|
kнт = e−158 (δn λ) = e−158 |
(1 2,6 30) |
= e−0,026 = 0,97 . |
|
9.Окончательно суммарный КИП проектируемой ПЗА равен:
σ= kаko kзkинтkнт ≈ 0,68 .
10.Площадь раскрыва зеркала:
S = πR2 |
= |
Gλ2 |
= |
|
104 9 |
≈1,2 10 |
4 см2 ; R ≈ 60 см. |
|
|
||||||
0 |
12,56 0,6 |
|
7,54 |
|
0 |
||
|
|
|
|
||||
11. Для определения ширины луча проектируемой ПЗА воспользуемся табл. 5.1, [1, с.113]:
∆θ0,5 ≈ 65oλ =1,625o.
D
Задание. Спроектировать и оценить точность изготовления параболической зеркальной антенны с коэффициентом усиления G = 27 дБ на частоте f = 3 ГГц с уровнем боковых лепестков, не
превышающим 25 дБ. Считать распределение поля по раскрыву параболическим. Величина фокуса параболы равна F = R0  2 .
2 .
Литература
1. Кочержевский Г.Н., Ерохин Г.А. Козырев Н.Д. Антенно-
фидерные устройства. - М.: Радио и связь,1989. - С. 133.
2. Айзенберг Г.З., Ямпольский В.Г. Антенны УКВ. - М: Связь, 1977. - Т. 1. - С. 325 - 326.
