9.3. Методы измерений.

Основное уравнение измерений мощности шумов имеет два неизвестных и . Именно поэтому значения мощности шумов и их отношений определяют методом совокупных измерений мощностей нескольких источников шумового излучения - генераторов шума (ГШ) по схемам рис. 9.1.а), б).

Рис.9.1 Измерение коэффициента шума .

а) -Измерение у ИЧ коэффициент шума

б) - Измерить неизвестную мощность генератора .

Измерения выполняют по процедуре, которую называют метод 2х отсчетов.

Имеется в виду, что измеряются два значения известной мощности шумов, выдаваемых мерами – генераторами шума и .

Рассмотрим обе задачи в совокупности на примере задачи 2.

Поскольку все мощности шумов можно выразить соответствующими температурами, то показания приемников можно записать.

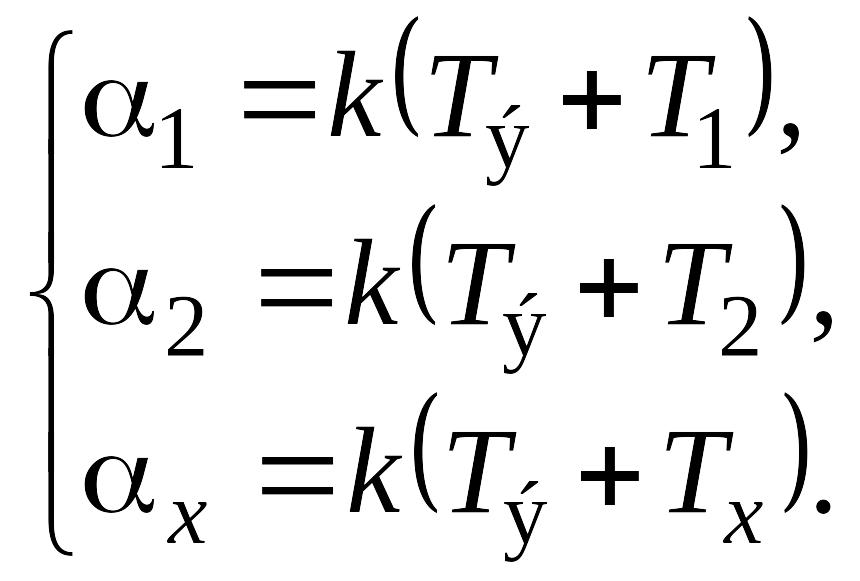(9.19)

Решая систему первых двух уравнений получаем

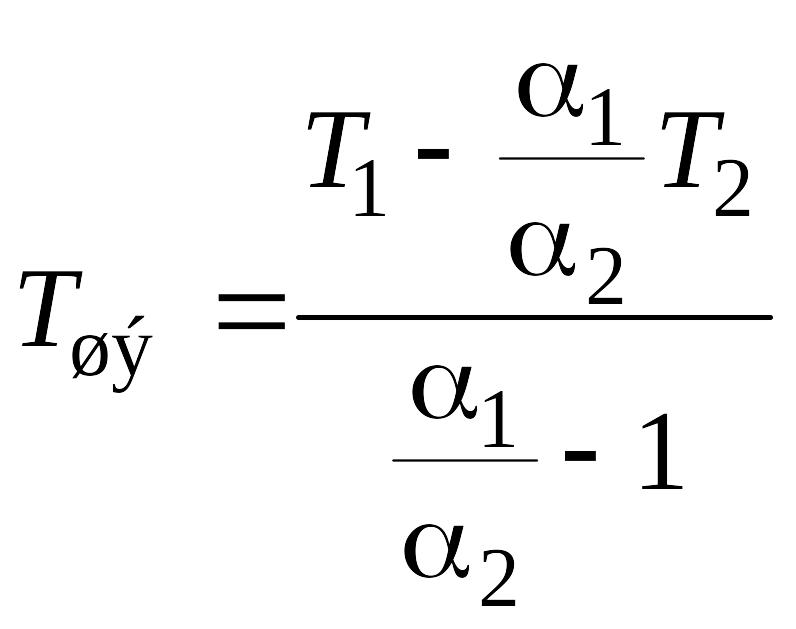. (9.20)

Это решение задачи №1.

Учитывая, что , если при измерении специально установить , то

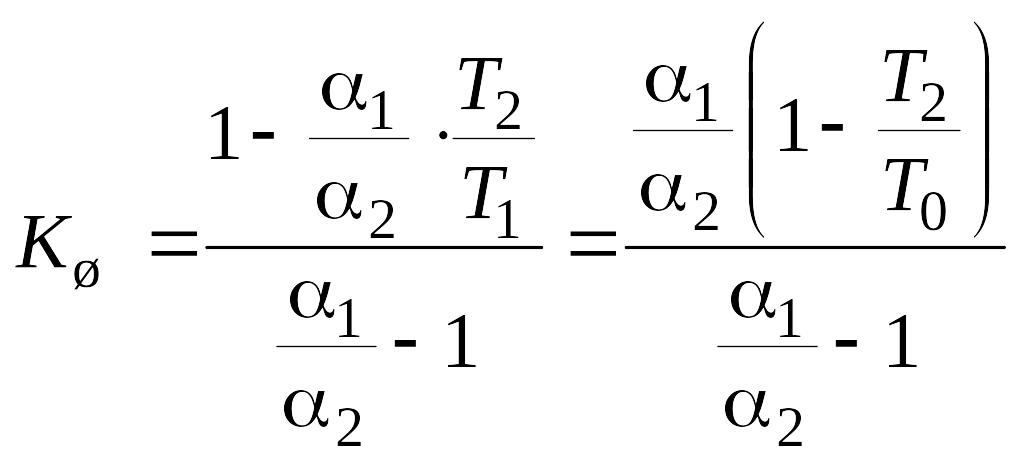. (9.21)

Таким образом, для измерения необходимы два ГШ, один из которых находится при стандартной температуре , а другой - при известной температуре .

Решая систему всех трех уравнений получим

. (9.22)

Это решение задачи №2.

Эту процедуру измерений можно записать в виде системы уравнений для мощностей , , , поступающих на вход измерителя мощности шумов, который выдает отсчеты показаний , , .

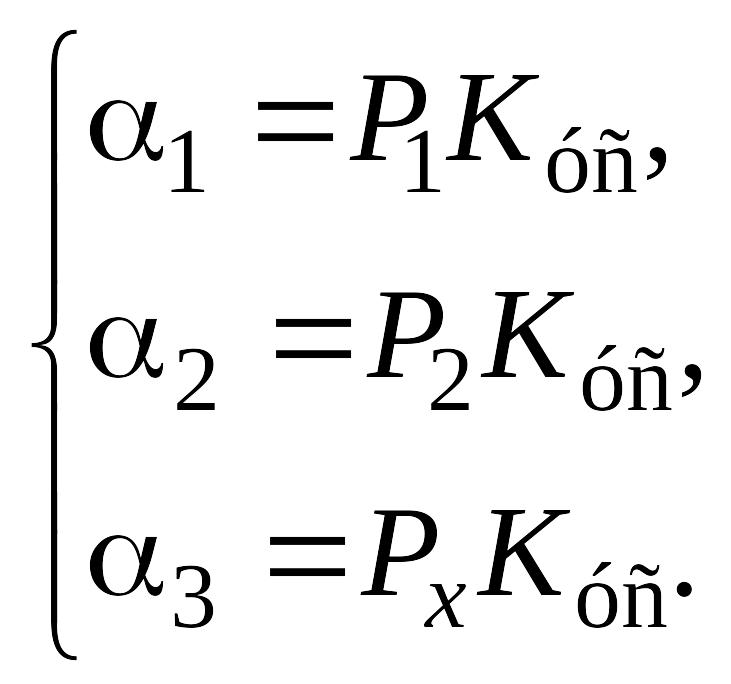или (9.23)

Из первых двух уравнений получаем решение для и , если считать, что и ,

или , (9.24)

где - мощность шумов, вносимая испытуемым 4х полюсником.

Описанный метод 2х отсчетов имеет недостаток, связанный с тем, что не учтены собственные шумы приемника – измерителя мощности, которые присутствуют даже в том случае, когда на его вход не поступает какой-либо шум от испытуемого устройства или испытуемых ГШ. При наличии шумов приемника уравнения следовало бы записать и решать в следующем виде:

(9.25)

Решение системы 2х уравнений при наличии шумов с температурой дает, считая что ,

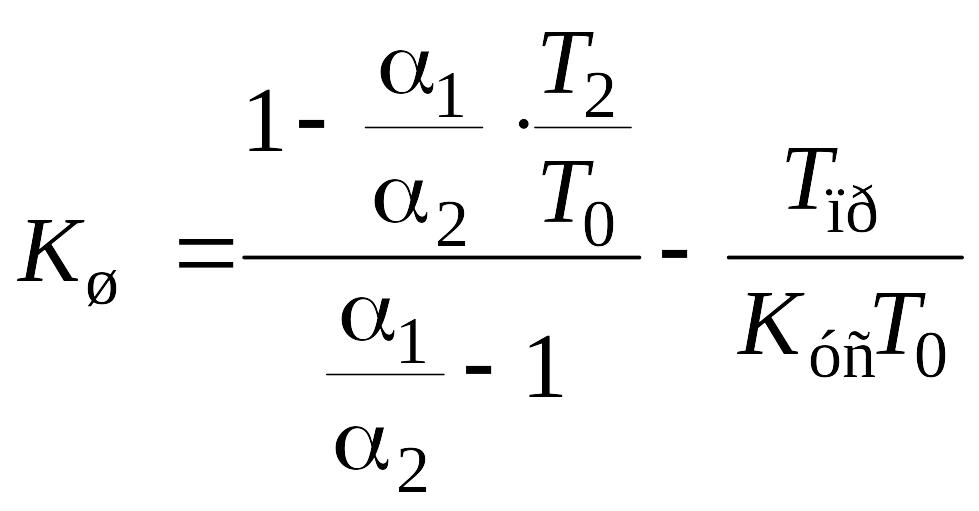; (9.26)

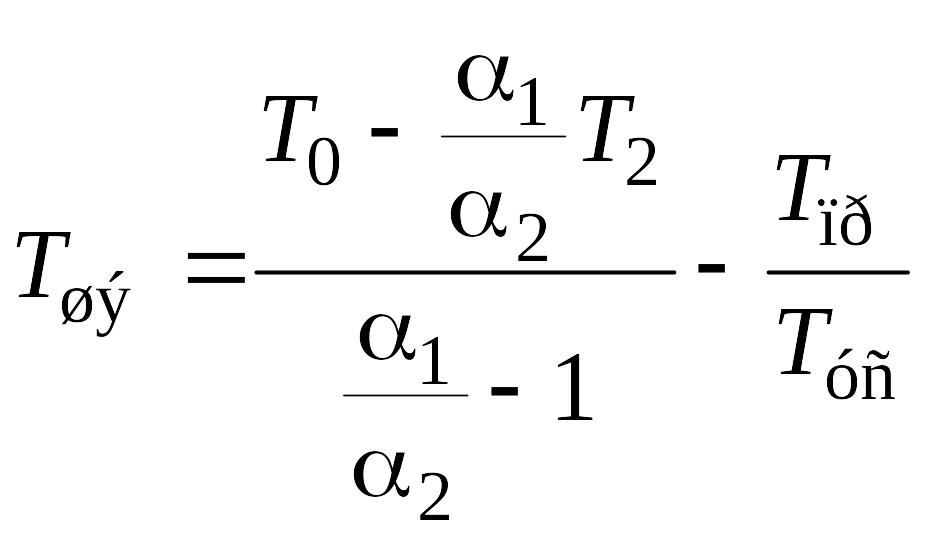. (9.27)

Таким образом, если неизвестны (как это чаще всего бывает) шумы приемник (измерителя мощности), измеряя и методом двух отсчетов, допускается абсолютная систематическая погрешность и относительное

(9.28)

или, что то же самое,

, (9.29)

. (9.30)

Для значений , рассчитанных по уравнениям, не учитывающим шумы приемника, допускается абсолютная систематическая погрешность

(9.31)

и относительная погрешность из-за не учета

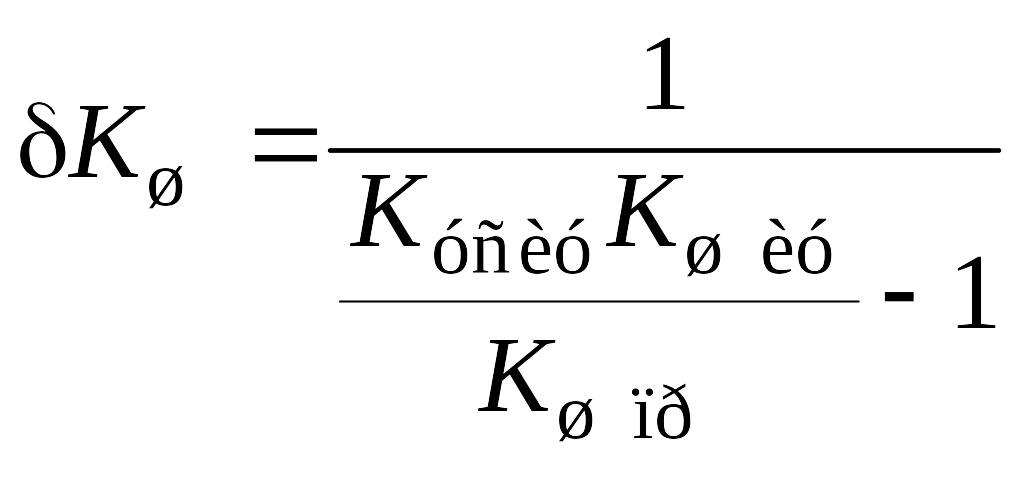. (9.32)

Из полученных соотношений следуют выводы:

1. При неизвестных и не исключенных процедурой измерений шумах приемника погрешности результатов измерений методом двух отсчетов тем меньше, чем больше испытуемого устройства и чем меньше собственные шумы приемника.

2. Чем меньше отношение коэффициента шума приемника к коэффициенту шума испытуемого устройства, тем меньше погрешность измерения .

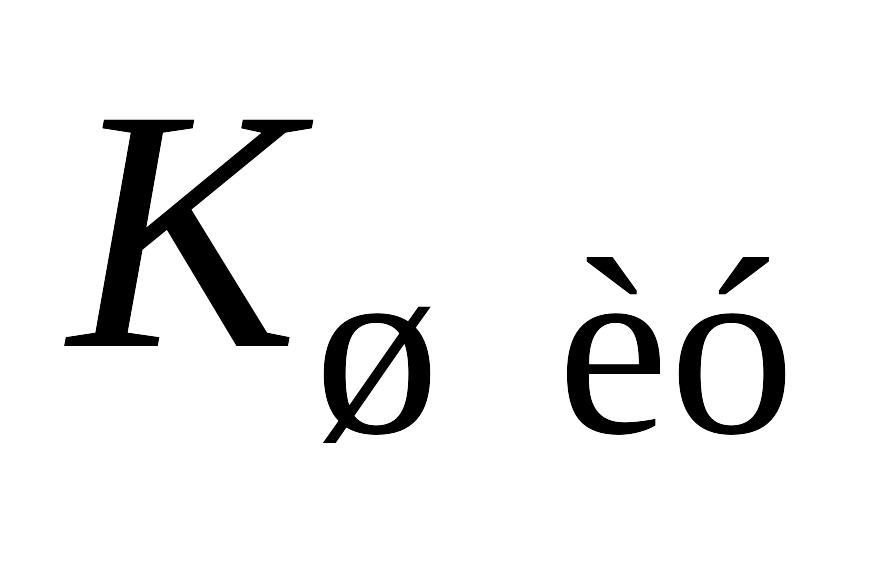Заметим, что абсолютная погрешность измерения коэффициента шума не имеет практического значения и не должна нормироваться при измерениях .

На погрешность результата измерений коэффициента шума и мощности шумов генератора шума методом 2х отсчетов влияют также следующие явления:

• инструментальные случайные погрешности измерений мощности - приемника;

• погрешности 2х значений мощности шума, выдаваемых мерами мощности шумов - генераторами шума;

• систематические погрешности измерения отношений , входящих в расчетные формулы, возникающие из-за нелинейности (зависимости от входной мощности);

• погрешности рассогласования, аналогичные погрешностям рассогласования при измерении мощности генераторов и ослабления фиксированных и переменных аттенюаторов.

Значения принято выражать в логарифмической шкале в децибелах, то есть как

(9.33)

или

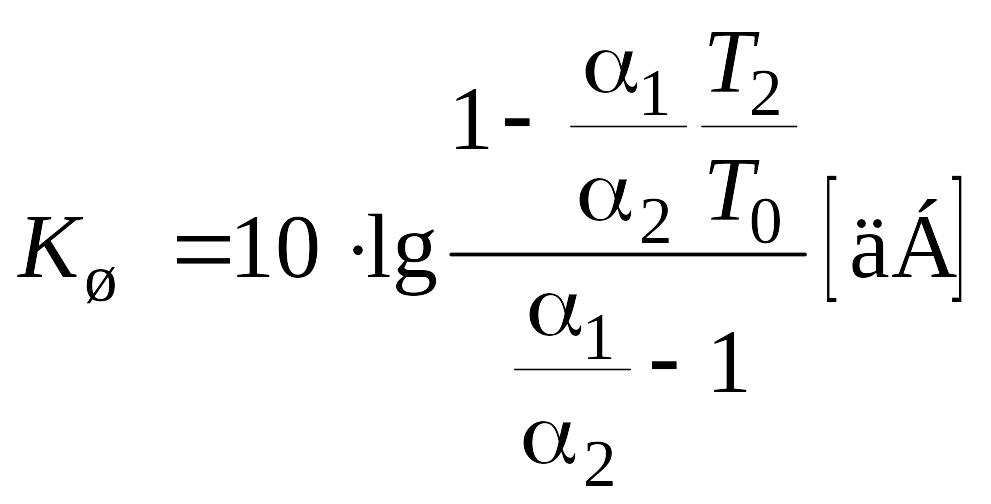. (9.34)

Соответственно, погрешности измерений выражают также в децибелах.

Например, 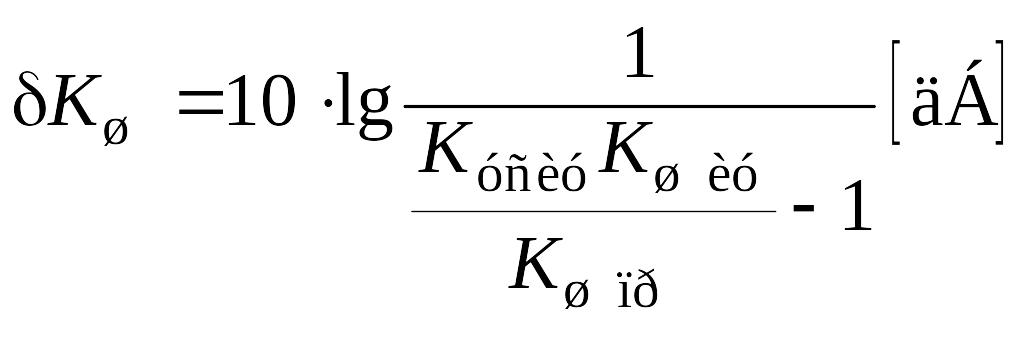, считая , выражается формулой

.