
- •В.Г.Чуйко Радиоэлектронные измерения
- •Глава один. Введение.
- •1.1. Предмет радиоизмерений.
- •1.2. Устройства радиотехники и электроники как объекты измерений.
- •1.3. Цели радиоизмерений
- •1.4. Измерительные задачи на различных стадиях научно-производственного процесса.
- •Глава два. Измерения. Погрешности измерений.
- •2.1. Понятие “измерение”.
- •2.2. Классификация измерений. Результат измерения.
- •2.3. Погрешности измерений и их классификация.
- •2.4. Систематические погрешности
- •2.5. Способы уменьшения систематических погрешностей
- •2.6. Случайные погрешности измерений
- •2.7. Способы оценивания и выражения случайных погрешностей.
- •Глава три Средства и методы измерений.
- •3.1. Классификация средств измерений.
- •3.2. Погрешности средств измерений.
- •3.3. Методы измерений.
- •3.4. Условия измерений.
- •Глава четыре. Радиоизмерения.
- •4.1. Классификация радиоизмерений.
- •4.2. Некоторые особенности радиоизмерений.
- •4.3. Классификация радиоизмерительных приборов по измеряемым величинам.
- •4.4. Классификация радиоизмерительных приборов по их месту в производственном процессе и условиям эксплуатации.
- •4.5. Вопросы выбора универсальных рип. Технические требования к рип. Нормируемые характеристики.
- •Глава пять. Составные части радиоизмерительных приборов.
- •5.1. Меры физических величин в радиоизмерительных приборах.
- •5.1.1. Меры частоты.
- •5.1.2. Меры напряжения постоянного тока.
- •5.1.3. Меры сопротивления на постоянном токе.
- •5.1.4. Меры емкости.
- •5.1.5. Меры индуктивности.
- •5.1.6. Меры мощности шумового излучения.
- •5.1.7. Меры волнового сопротивления и коэффициента отражения.
- •5.2. Преобразователи величин в радиоизмерительных приборах.
- •5.2.1. Масштабные преобразователи.
- •Делители напряжения.
- •Измерительные усилители.
- •Измерительные трансформаторы напряжения и тока.
- •Делители мощности.
- •Измерительные аттенюаторы.
- •Резистивные коаксиальные аттенюаторы.
- •5.2.2. Устройства визуализации результатов измерений.
- •5.2.3. Аналого-цифровые преобразователи.
- •Ацп интервал времени - цифровой код.
- •Ацп постоянное напряжение - интервал времени - цифровой код.
- •Ацп постоянное напряжение-частота.
- •Ацп поразрядного уравновешивания.
- •5.2.4. Преобразователь мгновенных значений переменного напряжения в цифру.
- •5.2.5. Аналоговый преобразователь мгновенных напряжений - электронно-лучевая трубка.
- •Осциллографические электронно-лучевые трубки.
- •Запоминающие трубки.
- •5.2.6. Преобразователи переменного синусоидального напряжения в постоянное.
- •5.2.7. Преобразователи импульсных напряжений в постоянное - Амплитудный детектор.
- •5.2.8. Выпрямительный детектор среднеквадратического значения.
- •Термоэлектрический преобразователь среднеквадратического значения.
- •Частотные детекторы.
- •5.2.9. Преобразователи разности фаз в постоянное напряжение - фазовый детектор.
- •5.2.10. Преобразователь измерения частоты в постоянное напряжение - частотный детектор.
- •5.2.11. Преобразователи мощности свч в постоянное напряжение.
- •5.3 Обобщенная структурная схема радиоизмерительного прибора.
- •5.3.1. Структурная схема прямого преобразования.
- •5.3.2. Структурная схема уравновешивающего преобразования.
- •5.3.3. Структурные схемы реальных приборов.
- •Глава шесть Измерения напряжений.
- •6.1. Вольтметры.
- •6.1.1 Вольтметры амплитудных значений.
- •6.1.2. Вольтметры среднеквадратических значений.
- •6.1.3. Вольтметры средневыпрямленных значений.
- •Особенности цифровых вольтметров переменного напряжения.
- •6.1.4. Вольтметры импульсных напряжений.
- •Компенсационные импульсные вольтметры.
- •6.1.5. Измерения нелинейных искажений
- •6.1.6. Измерения мгновенных значений переменного напряжения.
- •Основные нормируемые метрологические характеристики осциллографа.
- •6.2. Измерения частоты.
- •6.2.1. Меры частоты.
- •6.2.2. Электронносчетный частотомер.
- •6.2.3. Метод сравнения.
- •6.2.4. Гетеродинный частотомер.
- •6.3 Измерения разности фаз.
- •6.3.1 Фазовращатели - меры фазового сдвига.
- •6.3.2 Устройства сравнения.
- •6.3.3 Осциллографические измерения фазового сдвига.
- •6.3.4. Компенсационный метод измерения фазового сдвига.
- •6.3.5. Измеритель фазового сдвига с преобразованием во временной интервал.
- •6.3.6. Цифровой фазометр.
- •6.3.7. Измерения фазового сдвига с гетеродинным преобразованием частоты.
- •Глава семь Измерения мощности свч и ослаблений на свч.
- •7.1. Измерения мощности при высоких и сверхвысоких частотах в закрытых трактах.
- •7.2. Принципы и методы измерений. Основные аксиомы.
- •Измерительные задачи.
- •Принципы измерений.Физические явления, процессы, которые используют для измерений мощности свч.
- •Методы измерений.
- •7.3. Виды конструктивного исполнения ваттметров свч.
- •Обобщенная схема теплового ваттметра свч поглощаемой мощности.
- •7.4 Калориметрические измерители мощности.
- •Конструкции поглотителей и нагревателей.
- •Конструкции поглотителей и нагревателей проточных калориметров.
- •Конструкции измерителей приращения температуры.
- •Дифференциальная схема калориметра.
- •Блоки измерительные калориметрических измерителей мощности.
- •Источники и составляющие погрешностей калориметрических измерителей мощности.
- •7.5 Термоэлектрические ваттметры.
- •Преобразователи термоэлектрических ваттметров.
- •Измерительные блоки термоэлектрических и калориметрических ваттметров.
- •Погрешности метода.
- •Достоинства и недостатки метода.
- •Метод вольтметра.
- •Диодные преобразователи и измерительные блоки ваттметров.
- •Погрешности метода.
- •Достоинства и недостатки метода.
- •7.6 Термисторные ваттметры свч.
- •Конструкция волноводного первичного преобразователя.
- •Первичные измерительные преобразователи.
- •Волноводные термисторные преобразователи.
- •Основные технические характеристики волноводных термисторных преобразователей, используемых в практике измерений.
- •Измерительные блоки термисторных ваттметров.
- •7.7 Измерения ослабления
- •Метод отношения мощностей
- •Гетеродинные измерители ослабления. Измерительный приемник
- •Глава восемь Измерения коэффициента отражения.
- •8.1Области применения.
- •8.2. Определение физической величины. Понятие неоднородности тракта передачи волны.
- •Определение коэффициента отражения как измеряемой величины.
- •8.3 Измерительные задачи.
- •8.4. Принципы и методы измерений ксвн. Принципы измерений.
- •Метод измерений ксвн с помощью измерительной линии.
- •Методика измерений ксвн
- •Сравнение с мерой.
- •Погрешности результата измерений, получаемого с помощью измерительной линии.
- •8.5. Принцип и метод измерений модуля коэффициента отражения.
- •Метод измерений модуля коэффициента отражения “по определению”.
- •Погрешности измерений модуля коэффициента отражения рефлектометром.
- •Конструкция рефлектометра.
- •8.6 Автоматизация измерений с помощью рефлектометра.
- •Что такое автоматизация. Цели автоматизации измерений.
- •Пути, способы автоматизации.
- •Устройства, необходимые для автоматизации радиоизмерений на свч.
- •8.7 Панорамный измеритель коэффициентов отражений и передачи на свч.
- •Глава девять Измерения шумов электронных устройств.
- •9.1 Измерительные задачи.
- •9.2. Принципы измерения мощности шумов.
- •9.3. Методы измерений.
- •9.4 Метод измерительного аттенюатора – нулевой метод.
- •9.5 Нулевой модуляционный метод измерения .
- •9.5 Автоматизированные измерители коэффициента шума.
- •Глава десять. Обеспечение единства измерений.
- •10.1. Государственная система обеспечения единства измерений.
- •10.2. Нормативная база гси.
- •10.3. Организационные основы гси. Государственная метрологическая служба.
- •10.4. Метрологический контроль и надзор.
- •6.5. Эталоны
- •10.6. Поверочные схемы. Поверка и калибровка.
- •10.7. Метрологические характеристики средств измерений.
- •10.7. Методики выполнения измерений. Назначение методики выполнения измерений
- •Содержание документа на мви
- •Метрологическая экспертиза и аттестация документа на мви.
- •Заключение
- •Содержание
2.6. Случайные погрешности измерений
Случайная погрешность - это составляющая погрешности результата измерений, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений, проведенных с одинаковой тщательностью, одного и того же размера ФВ. Отметим следующие существенные стороны данного определения.
Случайные погрешности неизбежны и неустранимы и всегда присутствуют в результатах измерений. Они вызывают рассеяние результатов при многократном и достаточно точном измерении одной и той же величины, вызывая различие результатов в последних значащих цифрах результата.
Случайные погрешности - это погрешности, в появлении которых нет какой-либо закономерности, кроме той закономерности, что предсказать конкретное значение их в конкретном результате невозможно. Численные значения случайных погрешностей являются случайными числами.
Выявить наличие случайных погрешностей и их значения можно только выполняя повторные измерения, то есть, производя ряд измерений. Однако, априорное утверждение об их наличии бесспорно верное.
Имеются два фундаментальных положения, подтвержденных практикой:
при большом числе измерений случайные погрешности одинакового значения, но разного знака встречаются одинаково часто;
большие (по абсолютному значению) погрешности встречаются реже, чем малые.
Из первого положения следует важный для практики вывод, что при увеличении числа измерений случайная погрешность результата, полученного из ряда измерений, уменьшается вследствие того, что сумма погрешностей отдельных измерений данной серии стремится к нулю, то есть
![]() (2.4)
(2.4)
2.7. Способы оценивания и выражения случайных погрешностей.
Численное значение случайной погрешности является мерой рассеяния результатов измерений, то есть явления несовпадения результатов измерений одного и того же размера ФВ в ряду измерений. Экспериментальное оценивание случайных погрешностей производится путем формирования рядов равноточных измерений. В теории случайных величин предлагаются несколько характеристик рассеяния. Соответственно, имеется несколько способов выражения случайной погрешности.
Размах
результатов измерений
![]() - одна из наиболее простых оценок
рассеяния результатов единичных
измерений ФВ, образующих ряд (или выборку
из n
измерений), вычисляемая по формуле
- одна из наиболее простых оценок
рассеяния результатов единичных
измерений ФВ, образующих ряд (или выборку
из n
измерений), вычисляемая по формуле
![]() ,
где
,
где
![]() и
и
![]() - наибольшее и наименьшее значения ФВ
в данном ряду измерений. В некоторых
случаях, особенно при малых
- наибольшее и наименьшее значения ФВ
в данном ряду измерений. В некоторых
случаях, особенно при малых
![]() (
(![]() ),
размах является приемлемой оценкой
рассеяния результатов измерений, ибо
имеет связь со средней квадратической
погрешностью единичного измерения (в
ряду равноточных измерений).
),
размах является приемлемой оценкой
рассеяния результатов измерений, ибо
имеет связь со средней квадратической
погрешностью единичного измерения (в
ряду равноточных измерений).
Средняя квадратическая погрешность (СКП) единичного измерения (однократного измерения в ряду равноточных многократных измерений) - обобщенная характеристика рассеяния результатов, полученных в ряду независимых равноточных измерений одной и той же ФВ. вследствие влияния случайных погрешностей, вычисляемая по формуле:
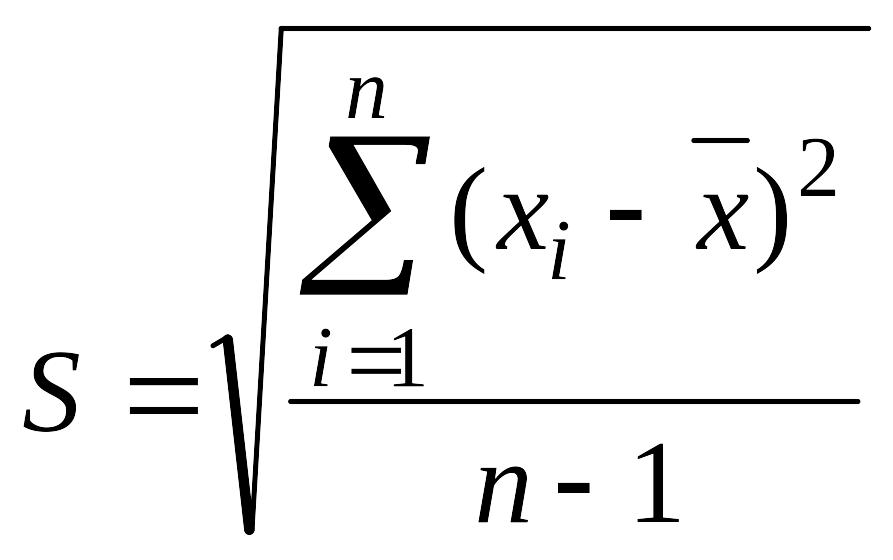 (2.5)
(2.5)
где S - средняя квадратическая погрешность единичного результата измерений, входящего в ряд из n измерений;
- результат отдельного измерения в ряду измерений;
![]() -
среднее арифметическое из результатов
n
измерений.
-
среднее арифметическое из результатов
n
измерений.
Средняя квадратическая погрешность является важнейшей для оценки достоверности результатов. Рассмотрим некоторые ее свойства, вытекающие из признания того, что со случайными погрешностями можно обращаться как со случайными величинами и использовать математический аппарат теории вероятностей и математической статистики.
Средняя квадратическая погрешность является эффективной оценкой погрешности измерений, то есть математическое ожидание величины
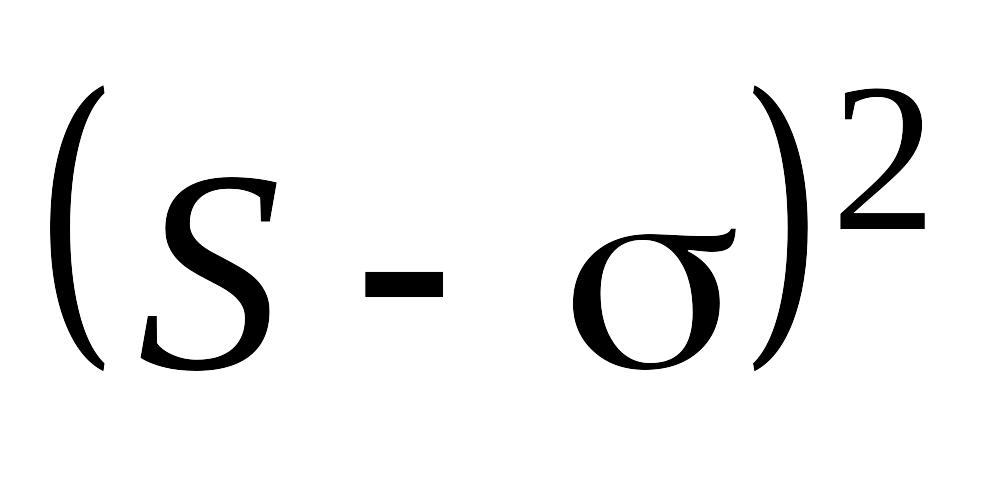 минимально.
минимально.Существует параметр рассеяния
 ,
который присущ генеральной совокупности
результатов измерений при числе
измерений
,
который присущ генеральной совокупности
результатов измерений при числе
измерений
 Значение СКП - S
Значение СКП - S ,
найденное по выборке конечного объема,
является приближенным значением
,
причем
,
найденное по выборке конечного объема,
является приближенным значением
,
причем
 .
В эксперименте с выборкой конечного
объема определяют не
,
а S,
но найденное значение S
является эффективной оценкой для
.
.
В эксперименте с выборкой конечного
объема определяют не
,
а S,
но найденное значение S
является эффективной оценкой для
.Для случаев, когда, для большей надежности получения удовлетворительного результата выполняют L-рядов равноточных рядов измерений, формула для вычисления СКП единичного измерения из всех рядов
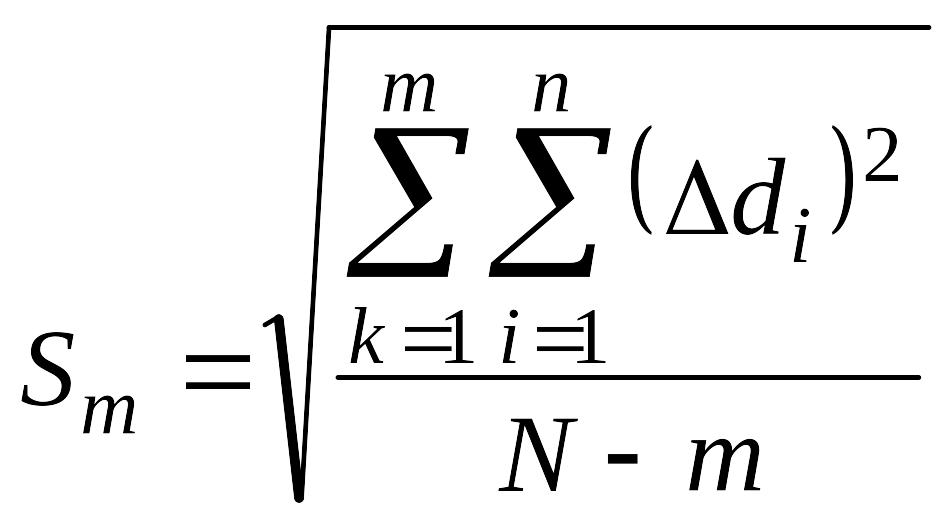 (2.6)
(2.6)
где
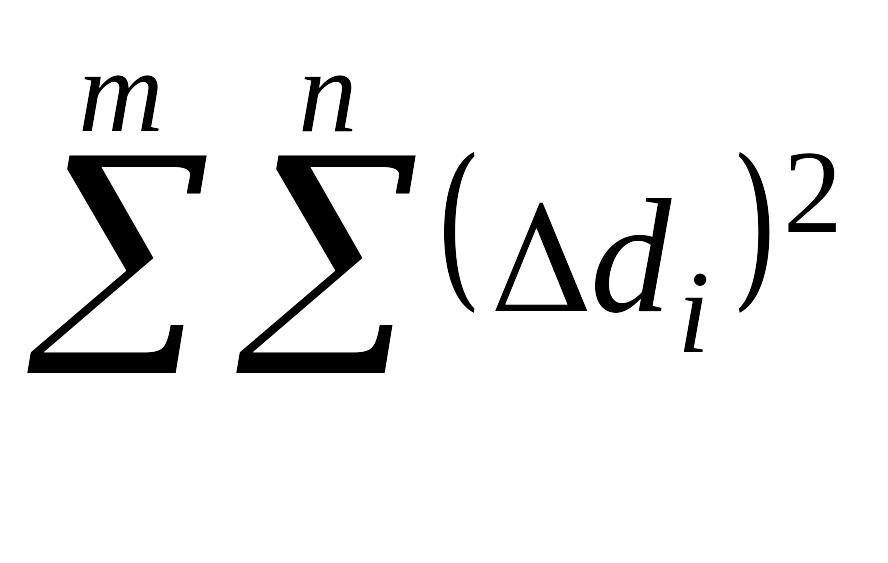 - сумма сумм квадратов отклонений от
средних значений в m
рядах;
- сумма сумм квадратов отклонений от
средних значений в m
рядах;
n - число измерений в ряду;
N - общее число измерений во всех рядах;
m - число рядов.
В практике при ограниченном числе измерений часто необходимо знать погрешность, с которой определяется значение СКП. В этом случае для нормального закона распределений (распределения Гаусса) применяются формулы:
 (2.7)
(2.7)
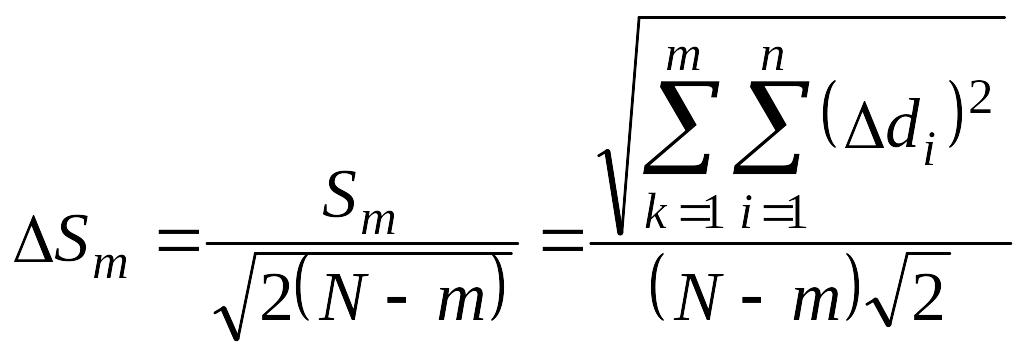 (2.8)
(2.8)
где
![]() и.
и.
![]() - соответственно средние квадратические
погрешности определения S
и
- соответственно средние квадратические
погрешности определения S
и
![]()
Средняя квадратическая погрешность результата косвенных измерений величины, выражаемой функцией
 измеряемых величин
измеряемых величин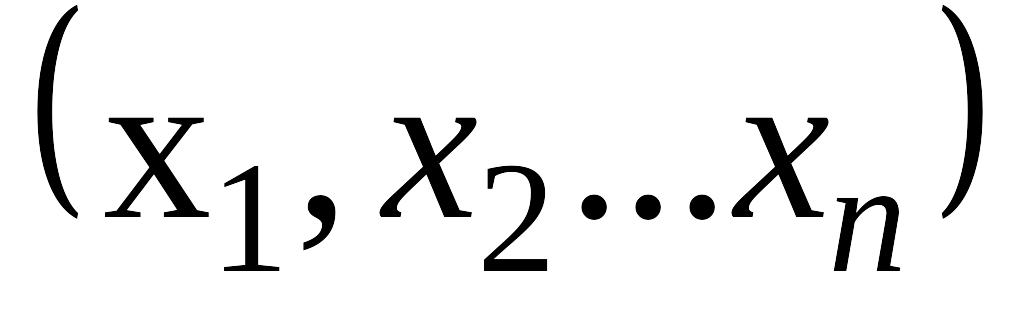 ,
вычисляется по формуле:
,
вычисляется по формуле:
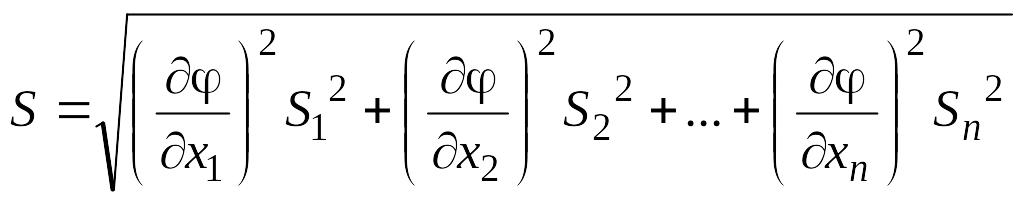 (2.9)
(2.9)
где
![]() - СКП результатов величин
- СКП результатов величин
![]() .
.
Если
сделан ряд измерений и результатом
измерения считается среднее арифметическое
значение n
результатов единичных измерений
,
то интерес представляет погрешность,
в том числе и СКП, среднего арифметического
-
![]() .
В отличие от СКП единичного измерения,
которую еще называют СКП ряда, величину
называют СКП результата (имея в виду,
что результат - это среднее арифметическое
ряда). Средняя квадратическая погрешность
результата измерений
,
полученного как среднее арифметическое
из ряда n
равноточных измерений, определяется
по формуле:
.
В отличие от СКП единичного измерения,
которую еще называют СКП ряда, величину
называют СКП результата (имея в виду,
что результат - это среднее арифметическое
ряда). Средняя квадратическая погрешность
результата измерений
,
полученного как среднее арифметическое
из ряда n
равноточных измерений, определяется
по формуле:
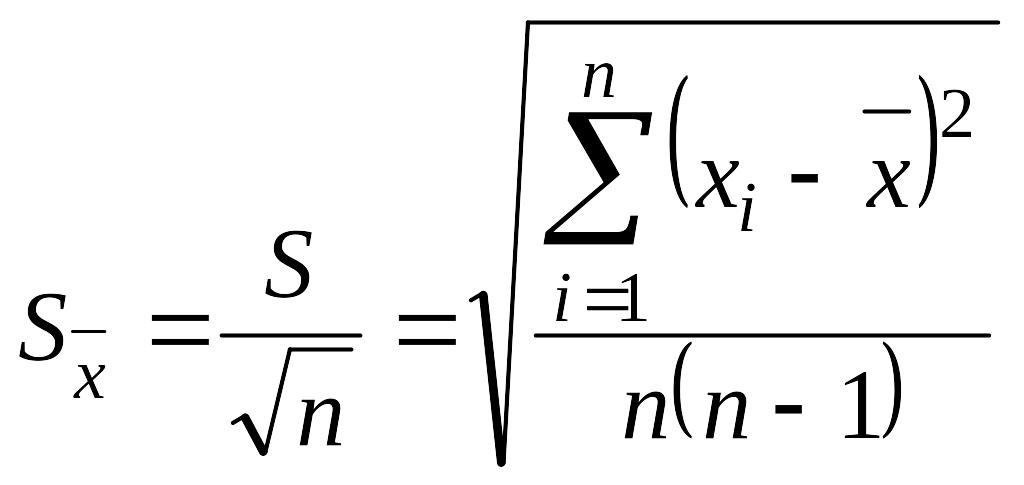 (2.10)
(2.10)
то
есть СКП среднего арифметического в
![]() раз меньше СКП единичного измерения.
раз меньше СКП единичного измерения.
Доверительный
интервал погрешности результата
измерений
- это интервал значений случайной
погрешности, внутри которого с заданной
вероятностью находится искомое (истинное)
значение погрешности результата
измерений. Доверительный интервал
определяется зоной, равной
![]() для каждого измерения в ряду измерений
и
для каждого измерения в ряду измерений
и
![]() для результата измерений как среднего
арифметического. Значение величин S
и
- для каждого ряда измерений является
также случайной величиной. Распределение
этой случайной величины описывается
законом Стъюдента с плотностью
вероятности, зависящей от числа измерений
n.
для результата измерений как среднего
арифметического. Значение величин S
и
- для каждого ряда измерений является
также случайной величиной. Распределение
этой случайной величины описывается
законом Стъюдента с плотностью
вероятности, зависящей от числа измерений
n.
На
практике часто необходимо решить
следующую задачу - определить с заданной
вероятностью доверительный интервал
для случайной погрешности результата
n
измерений, полученного как среднее
арифметическое. Начальное условие -
задается вероятность, с которой внутри
определяемого (искомого) интервала
располагается результат. Если результат
является средним арифметическим
значением результатов n
единичных измерений, то определяют
,
то есть СКП результата. Поскольку
распределена по закону Стъюдента, то
по таблицам табулированных значений
этого распределения определяют на какое
число t
необходимо умножить значение
,
чтобы с заданной вероятностью P
истинное значение измеряемой величины
находилось в интервале
![]() .
.
Средняя арифметическая погрешность единичного измерения (в ряду измерений) - это обобщенная характеристика рассеяния отдельных результатов равноточных независимых измерений, входящих в ряд из n измерений, вычисляемая по формуле:
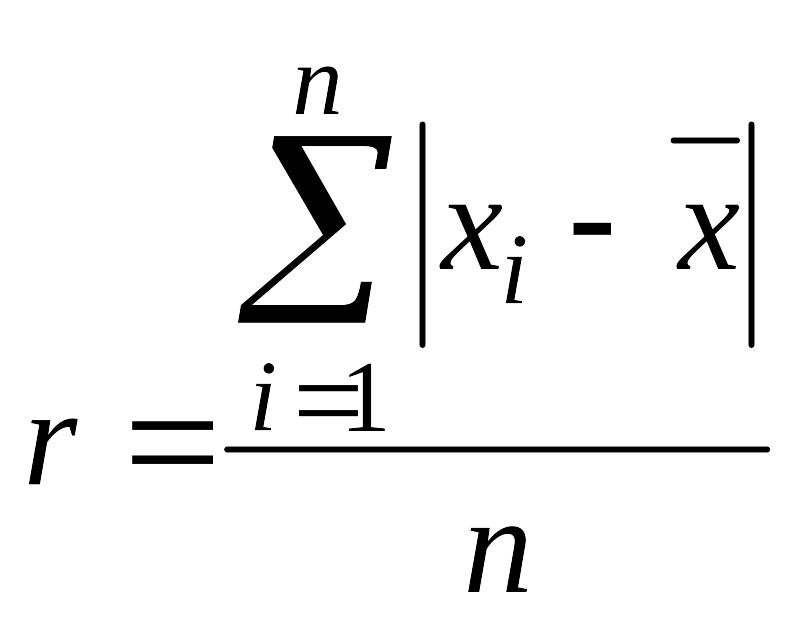 (2.11)
(2.11)
где r - средняя арифметическая погрешность;
- результат i-го измерения, входящего в ряд измерений;
![]() -
среднее арифметическое из n
значений величины;
-
среднее арифметическое из n
значений величины;
![]() -
абсолютное значение погрешности i-го
измерения.
-
абсолютное значение погрешности i-го
измерения.
В заключение приведем соотношения, связывающие СКП с размахом и средней арифметической погрешностью. Если рассеяние результатов измерений подчиняется нормальному распределению, то математическое ожидание для средней арифметической погрешности:
![]() (2.12)
(2.12)
Поэтому можно приближенно считать, что
![]() (2.13)
(2.13)
связь СКП с размахом можно выразить приближенной формулой
![]() ,
,
которая
с достаточной для технических измерений
точностью справедлива при
![]() .
Более точно можно записать:
.
Более точно можно записать:
![]()
где C зависит от числа измерений и определяется из таблицы:
Точность результата измерений - это характеристика качества измерения, отражающая близость к нулю погрешности его результата. "Точность" - термин распространенный, особенно, в повседневном техническом языке. Он отражает некоторое обобщенное образное представление о результате измерения. Обычно имеют в виду, что чем меньше погрешность результата, тем больше его точность.
Точность результата измерений обусловлена несколькими основными факторами:
свойствами и качеством средств измерений;
внешними условиями измерений;
принятыми методами измерений;
квалификацией операторов при ручных (неавтоматизированных) измерениях.
Кратко рассмотрим эти факторы в следующих разделах.
