5.3.2. Структурная схема уравновешивающего преобразования.

Особенность схемы состоит в том, что выходная величина , как показано на рис. 5.33, подвергается обратному преобразованию в величину , однородную с входной величиной и уравновешивающей ее, в результате чего на вход цепи прямого преоразования поступает только небольшая часть входной величины . Другими словами, используется отрицательная обратная связь и уравновешивание производится автоматически.

Возможны два режима работы: режим неполного уравновешивания и режим полного уравновешивания. Рассмотрим сначала первый из них.

Прежде всего получим для схемы уравнение преобразования . Для этого запишем уравнение связи между сигналами в различных участках схемы. Будем считать справедливыми те же упрощающие предположения в отношении линейности звеньев, которые были приняты при анализе схемы прямого преобразования. Можно записать:

(5.69)

уравнение цепи прямого преобразования:

(5.70)

уравнение цепи обратного преобразования:

(5.71)

Искомое уравнение измерительной схемы будем искать в виде:

(5.72)

где - коэффициент преобразования измерительной схемы.

Выразив из (5.12) и подставляя , , из (5.69), (5.70), (5.71), получим

(5.73)

(5.74)

Таким образом, выходной сигнал пропорционален входному и зависит от коэффициентов преобразования как цепей прямого, так и обратного преобразования.

Можно видеть, что при

(5.75)

то есть цепь прямого преобразования слабо влияет на работу схемы. Для достижения высокой чувствительности следует уменьшить , а для выполнения условия следует увеличить К.

Определим мультипликативную погрешность, обусловленную нестабильностями K и . Определим относительную погрешность как погрешность косвенного измерения:

(5.76)

(5.77)

так как . Суммируя (5.16) и (5.17) и переходя к конечным приращениям, получаем:

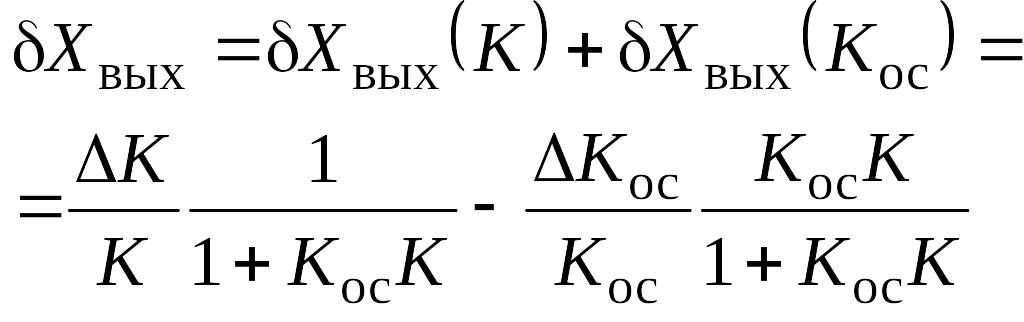(5.78)

Относительная мультипликативная погрешность состоит из суммы двух членов, один из которых пропорционален суммарной погрешности всех преобразователей цепи прямого преобразования, а другой - суммарной погрешности цепи обратной связи. При погрешность из-за нестабильности K уменьшается в раз. Погрешность, обусловленная нестабильностью цепи обратной связи, почти полностью входит в суммарную погрешность. Следовательно, в прямой цепи можно использовать менее стабильные преобразователи, например, усилители, если будет выполнено условие . В цепи обратной связи необходимо использовать преобразователи с высокой стабильностью, например, пассивные делители и т. п.

Заметим, что коэффициент преобразования схемы уравновешивающего преобразования в раз меньше, чем коэффициент преобразования схемы прямого преобразования. Поэтому для получения равных значений величины в схеме с обратной связью необходимо увеличивать коэффициент преобразования (усиления) цепи прямого преобразования в раз по сравнению со схемой без обратной связи. Отметим, что имеются пределы увеличения K, обусловленные динамическими характеристиками (динамическими погрешностями) схем. Уравнение (5.78) показывает также, что, благодаря введению отрицательной обратной связи, уменьшается нелинейность функции прямого преобразования.

Оценим теперь аддитивную погрешность, обусловленную дрейфом нуля, наводками, помехами, порогом чувствительности звеньев. Введем в структурную схему дополнительные сигналы , . Приведем эти сигналы ко входу схемы. Тогда аддитивная абсолютная погрешность выразится в виде:

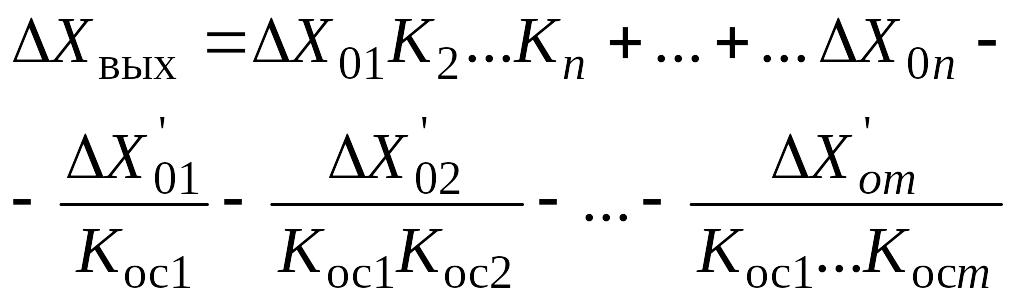(5.79)

Можно видеть, что аддитивная погрешность не зависит от глубины обратной связи и не может быть уменьшена по абсолютной величине введением уравновешивающего преобразования. При увеличении глубины обратной связи будет уменьшаться чувствительность и соответственно возрастать верхний допускаемый предел входной величины.

Применение схемы уравновешивающего преобразования является действенным путем повышения точности РИЛ, широко применяется на практике и является основой создания автоматических измерительных приборов.

Рассмотрим теперь режим полного уравновешивания, когда . Это возможно в том случае, когда в цепи прямого преобразования имеется интегрирующее звено с функцией преобразования такой, что . Измерительные устройства с ручным уравновешиванием можно также рассматривать как имеющие структурную схему уравновешивающего преобразования с полным уравновешиванием.

Уравнение преобразования для такого случая очевидно, запишется:

(5.80)

Коэффициент преобразования схемы полностью определяется цепью обратного преобразования и не зависит от цепи прямого преобразования. Мультипликативная относительная погрешность, связанная с нестабильностью коэффициентов преобразования звеньев

(5.81)

обусловлена только цепью обратной связи. Аддитивная погрешность схемы полного уравновешивания почти полностью определяется порогом чувствительности звеньев. Под порогом чувствительности звена понимают минимальный сигнал на входе, способный вызвать сигнал на выходе. При входном сигнале меньше порога чувствительности сигнал на выходе не появляется, следовательно, уравновешивание происходит при , где - порог чувствительности звеньев в цепи прямого преобразования до интегрирующего звена включительно.

Аддитивная погрешность схемы полного уравновешивания запишется как:

(5.82)

где - порог чувствительности интегрирующего звена.

Заметим, что введение понятия порога чувствительности является приемом, позволяющим представить в качестве линейного фактически нелинейное устройство с характеристикой, имеющей зону нечувствительности (рис. 5.34).