5.2.3. Аналого-цифровые преобразователи.

Цифровые устройства визуализации - это табло, на которых изображается текущее значение измеряемой величины в виде цифры и наименования единицы, например, 4,321 [В], или 0,587 Вт, или 3861 кГц и т. д. В основу цифровых устройств визуализации положены преобразователи код-цифра. Обычно используется двоичный код числа, выражающего значения постоянного напряжения или частоты, которые вырабатываются аналого-цифровыми преобразователями (АЦП) постоянного напряжения или электронно-счетными частотомерами (счетчиками ЭСЧ). Электронная промышленность выпускает десятки модификаций интегральных схем, выполняющих функции АЦП и ЭСЧ.

В качестве устройств визуализации в некоторых измерительных приборах и измерительных системах, представляющих результаты в виде кодов или цифровом виде, используются мониторы компьютеров. Таким образом, для того, чтобы представить результаты измерений с высокой разрешающей способностью и в форме, удобной для хранения и обработки необходимы АЦП и ЭСЧ, а также преобразователи измеряемых величин в постоянное напряжение и (или) частоту.

Цифровые устройства визуализации используют преобразователи постоянного напряжения (аналого-цифровые преобразователи АЦП) в цифровой код, материализуемый в виде числа (совокупности) импульсов положительной и отрицательной полярности или состояний элементов электронных схем, например, триггеров, которым присваивается значение информационной единицы (“1”) или нуля (“0”) в двоичной системе счисления. В качестве аналоговой величины, преобразуемой в цифровой код, чаще всего выбирают постоянное напряжение или длительность интервала времени.

Рассмотрим простейшие АЦП временного интервала τ [с] и постоянного напряжения U [B].

Ацп интервал времени - цифровой код.

Сущность аналогового преобразования интервала времени состоит в том, что измеряемый интервал τ сравнивают с образцовым интервалом, воспроизводящим единицу времени. Это достигается заполнением измеряемого интервала импульсами с калиброванным периодом следования . Интервал времени представляется пропорциональным ему числом импульсов.

Структурная схема АЦП, реализующего такое преобразование, приведена на рис. 5.9.

Рис. 5.9 Структурная схема АЦП.

Преобразуемый интервал представляется промежутком време­ни между двумя импульсами, которые могут быть либо от одного источника, либо от разных. Эти импульсы подаются на триггер. Если импульсы, задающие интервал, поступают от разных источ­ников, применяется триггер с раздельными входами; если от од­ного - триггер со счетным входом. В исходном состоянии тригге­ра (0) на вход 2 временного селектора подается отрицательное напряжение. Импульсы, калиброванные по периоду следования (счетные импульсы), поступают на вход 1 временного селектора. При отрицательном напряжении, на входе 2 они не могут пройти на выход. С приходом первого импульса (опорного) триггер пере­брасывается в состояние 1, при котором на входе 2 появляется положительное напряжение. Счетные импульсы начинают посту­пать с выхода временного селектора. С приходом интервального импульса, задающего конец интервала времени, триггер перебра­сывается в состояние 0 и поступление счетных импульсов с вы­хода временного селектора прекращается. На рис. 5.9,б приве­дена временная диаграмма сигналов, действующих в схеме преоб­разователя. Триггер в результате двухкратного переброса форми­рует прямоугольный импульс с крутыми фронтами, равный по дли­тельности преобразуемому интервалу времени. Этот импульс на­зывают стробирующим. За время действия строб-импульса с вы­хода селектора на счетчик импульсов поступают счетные им­пульсы.

Обозначим период счетных импульсов , их частоту ; при число импульсов m на выходе временного селектора будет

(5.12)

и

, (5.13)

где mТ - число целых периодов, которые укладываются в интервале, Ent() - обозначает целую часть.

Уравнение (5.12) есть уравнение преобразования. Оценим погрешность преобразования интервала времени в число импульсов.

Из уравнения (5.13), принимая во внимание существо метода преобразования, можно выразить реализацию относительной погрешности определения временного интервала δτ в виде , где - относительная методическая погрешность, обусловленная тем, что, во-первых, не учитывается дробная часть периода счетных импульсов, во-вторых, за число периодов берется число импульсов (погрешность дискретности); - относительная погрешность, с которой известен период счетных импульсов.

Оценим сначала погрешность дискретности - абсолютная погрешность дискретности.

Из рис. 5.10, где показано заполнение интервала счетными импуль­сами, видно, что

,(5.14)

поскольку .

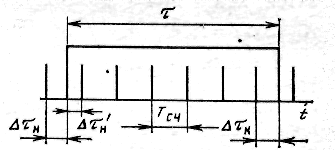
Рис. 5.10

Соотношение (3) можно рассматривать как точное значение преобразуемого интервала τ, выраженное через измеренное зна­чение , и некую реализацию погрешности дискретности . Составляющие погрешности дискретности и возникают в начале и конце интервала τ. Момент прихода счетного импульса не связан с моментом начала преобразуе­мого интервала. Поэтому может принимать любые значения от 0 до , все значения будут равновероятны. Следовательно, составляющая погрешности дискретности является случайной пог­решностью, распределенной в границах от 0 до по равнове­роятному закону.

Плотность распределения вероятности выражается, как

. (5.15)

Выделим систематическую погрешность, определив математичес­кое ожидание погрешности :

. (5.16)

Центрированная случайная погрешность будет изменяться в границах . Среднее квадратическое зна­чение погрешности

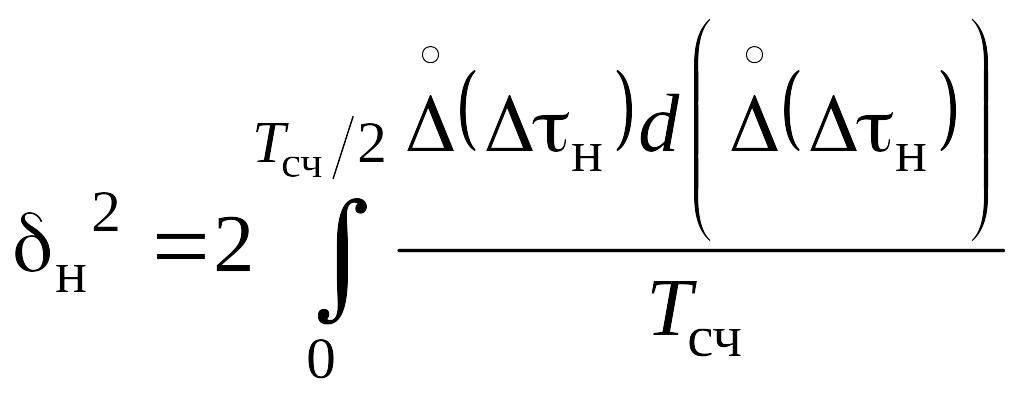; (5.17)

(5.18)

Так как интервал τ неизвестен, то погрешность так же, как и , будет распределена по равновероятному закону в границах . Поэтому систематическая составляющая погрешности и среднее квадратическое значение случайной составляющей выра­зятся, как

, . (5.19)

Выражения для и δ погрешности дискретности начала и конца совпадают с выражениями для погрешности кван­тования по значению. В данном случае также имеет место процесс квантования. Поскольку измеряемой величиной является интервал времени, мы называем ее погрешностью дискретизации или дис­кретности.

Суммарная погрешность дискретности , очевидно, не будет содержать систематической погрешности. Поскольку слу­чайные погрешности и статистически независимы и обе распределены по симметричному закону равной вероятности с равными границами , суммарная случайная погрешность будет распределена по треугольному закону. Среднее квадратическое значение

. (5.20)

Таким образом, относительная погрешность дискретности

. (5.21)

Погрешность дискретности обратно пропорциональна длитель­ности интервала и прямо пропорциональна периоду счетных им­пульсов. Оценим теперь погрешность . Эта погреш­ность обусловлена, главным образом, нестабильностью частоты генератора счетных импульсов, который включает в себя высоко­стабильный генератор с кварцем и формирователь коротких им­пульсов. Систематическую составляющую нестабильности исклю­чают периодической корректировкой частоты генератора. Поэтому погрешность рассматривают как случайную со средним квадратическим значением, равным среднему квадратическому значе­нию относительной нестабильности частоты распре­деленную нормально.

В результате получаем выражение для средней квадратической погрешности преобразования

. (5.22)

Заметим, что влияние второго слагаемого больше при преобразовании интервалов времени большей длительности, а первого - при преобразовании интервалов малой дискретности.