Добавил:

MagnuM Закончил бакалавриат по специальности 11.03.01 Радиотехника в МИЭТе. Могу помочь с выполнением курсовых и БДЗ по проектированию приемо-передающих устройств и проектированию печатных плат. Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Радиотехнические системы

Файл:

Литература / Лекции РТС старые.pdf

Скачиваний:

Добавлен:

10.09.2023

Размер:

3.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Лекция 8.

Дальность действия и период следования импульсов. Понятие разрешающей способности РЛС.

План лекции:

-Cоотношение максимальной дальности действия РЛС и длительности импульсов;

-Разрешение по дальности;

-Угловая разрешающая способность;

-Разрешающая способность по радиальной скорости цели, разрешаемый объем и площадка.

Дальность действия РЛС

О выборе периода следования импульсов передатчика. Для того чтобы дальность до цели измерялась однозначно и просто, нужно выбирать период следования импульсов передатчика из соотношения

T сл >	2Rmax
	c	(2.4).

Здесь Rmax - дальность действия радиолокатора. При нарушении условия (2.4) возникает неопределенность в измерении дальности цели, иллюстрируемая на рис.2.6. Здесь показано расположение импульсов отраженного сигнала

	цели относительно импульсов передатчика. Рис.2.6a относится к случаю, когда
T cл >	2Rmax	, а рис.2.6, б - к случаю	T сл<		2Rmax	. На рис.2.6, б пунктиром изображен

	c				c
отраженный сигнал, обязанный импульсу передатчика, который
	предшествует первому зондирующему импульсу. Из рис.2.6, б следует, что
измеренная дальность цели равна R				. Истинная дальность составляет R2 .
	1

Ut	Ut
	Ur
	t
2Rmax
C	Tp
	Tp
	(a)
Ut	Ut
Ur	Ur
	t
	2R1
2R	C
2R	2
C	(b)
	(b)

Рис. 2.6. Расположение импульсов сигнала цели относительно импульсов передатчика.

Разрешающая способность радиолокатора

Разрешающей способностью называют свойство радиолокатора раздельно обнаруживать близко расположенные цели и раздельно измерять их координаты и радиальные скорости. Вместе с тем термин "Разрешающая способность" используется и как количественная характеристика степени разрешения по той или иной координате цели. В этом случае разрешающей способностью по какой либо координате (дальности, азимуту, углу места) или радиальной скорости называют минимальную разность значений этой координаты (скорости) двух целей, при которой эти цели могут быть еще обнаружены раздельно. При этом, конечно, считается, что остальные координаты (скорость) целей одинаковы или, во всяком случае, по ним цели не разрешаются.

В данном разделе кратко рассматриваются факторы, определяющие разрешающую способность радиолокатора по дальности, угловым координатам и радиальной скорости. Кроме того, здесь вводятся понятия разрешаемого объема и разрешаемой площадки радиолокатора.

Разрешение по дальности

Оценим разрешающую способность по дальности на примере импульсного радиолокатора. Пусть имеются две цели на дальностях R1 и R2 (рис.2.7.а). Временной зазор между импульсами отраженных сигналов на выходе устройства обработки (рис.2.7.б) равен

t	з	=	2	(R	2	− R )	− τ	вых		(2.5)
	з		c		2	1		вых
								Цель1	Цель 2
РЛС
						R1
								R2
								(a)
									τвых
								Ur1	Ur 2	t
										t
						2R1			t з
						C		2R2
								2R2
								C
								(b)

Рис. 2.7. К расчету разрешения РЛС по дальности. а) Расстояния целей до РЛС б) Временные интервалы

Здесь τвых - длительность импульса отраженного сигнала на выходе устройства обработки. При сближении целей, как следует из (2.5), промежуток t з уменьшается.

Примем за разрешающую способность по дальности ∆R такую разность дальностей целей R2 – R1, при которой t з обращается в нуль и отраженные сигналы

начинают сливаться. Тогда из (2.5) следует, что				2∆R	= τвых и
начинают сливаться. Тогда из (2.5) следует, что				c	= τвых и
				c
∆R =	cτвых	.	(2.6)
∆R =		.	(2.6)
2

Длительность импульса на выходе согласованного фильтра равна τвых ≈ ∆1f c , где

∆f c - полоса пропускания согласованного фильтра. Следовательно, при использовании согласованного фильтра в устройстве обработки сигналов

∆R =	c	(2.7)
	2 ∆f c

Угловая разрешающая способность

Угловая разрешающая способность равна ширине двусторонней диаграммы направленности антенной системы РЛС - θ. Действительно, при угловом расстоянии между двумя объектами, равном θ, эти объекты не могут одновременно попасть в пределы луча антенны. В разделе 2.5 будет рассмотрен метод значительного улучшения угловой разрешающей способности при обзоре земной поверхности из космоса.

Разрешающая способность по радиальной скорости целей В соответствии с (2.2) радиальная скорость цели выражается через доплеровское

смещение частоты

VR = λ2 fd .

Следовательно, разрешающая способность радиолокатора по скорости равна

∆V =	λ		∆f		d .	(2.8)
R	2				d .	(2.8)
Здесь ∆fd - разрешение по доплеровскому смещению частоты.
Величина ∆fd обратна длительности когерентной пачки отраженного сигнала
N · Tсл. Следовательно,
∆VR =	λ		1
∆VR =	2 NTсл					(2.9)
	2 NTсл					(2.9)
В случае некогерентного сигнала ∆fd		обратна длительности одного импульса
пачки τи. Следовательно
∆VR =				λ
∆VR =				2τи .
				2τи .

Разрешаемый объем и разрешаемая площадка

Для комплексного описания пространственной разрешающей способности радиолокатора используют понятия разрешаемого объема и разрешаемой площадки. Разрешаемый объем - это область трехмерного пространства, все точки которой не разрешаются. Иными словами, сигналы от отражателей, находящихся внутри данного объема, одновременно присутствуют на входе радиолокационного приемника. Сумма их мощностей представляет собой результирующий сигнал.

Разрешаемый объем имеет вид усеченного конуса с длиной образующей, равной ∆R, и телесным углом при вершине, равным раствору двусторонней ДН антенны по половинной мощности (рис.2.8.).

РЛС	R θ1	R θ2
	R
		ΔR

Рис.2.8. Разрешаемый объем РЛС. Величина разрешаемого объема приблизительно равна

∆W =	π	∆R R2	θ θ	2 .	(2.10)
	4		1	2 .	(2.10)

В формуле (2.10) R - дальность от радиолокатора до разрешаемого объема, θ1 и θ2 - значения ширины ДН антенн в двух взаимно перпендикулярных плоскостях (в радианах).

Если рассматриваются отражатели на плоскости, то в качестве меры пространственного разрешения используется понятие разрешаемой площадки. Разрешаемая площадка - это трапеция ABCD на рис.2.9, все точки которой не разрешаются радиолокатором

РЛС
θ1	R
		ΔR
	D	C
	A	ε
	A
		B

Рис.2.9. Разрешаемая площадка РЛС.

Сумма мощностей всех отражателей в пределах разрешаемой площадки формирует результирующий сигнал на входе приемника. Величина разрешаемой площадки приблизительно равна

∆S =	∆R	Rθ
	cosε		(2.11)
		1

В формуле (2.11) θ1 - ширина ДН антенны (в радианах), ε - угол места луча антенны.

Пример определения разрешающей способности РЛС.

Определите зависимость и постройте график зависимости разрешающей способности импульсной РЛС по дальности от базы сигнала.

Графики постройте в диапазоне изменения базы сигнала B =1÷20 с шагом 1 для длительностей сигнала tc = 0,5; 1; 1,5; 2 мкс.

Решение:

Разрешающая способность по дальности в радиолокации определяется по длительности импульса после согласованного фильтра ∆R = 2c*tBc .

В результате получаем наборы значений и построенное по этим наборам семейство кривых зависимости разрешающей способности РЛС по дальности от базы сигнала.

Delta R=DeltaR(B)

300
250
200
R,[m]
150
Delta
100
50
0	0	2	4	6	8	10	12	14	16	18	20
						B, [åä]

Зависимость разрешающей способности по дальности импульсной РЛС от базы сигнала для различных значений длительности сигнала.

Задание на самостоятельную проработку

Ознакомится с рекомендуемой литературой и конспектом данной и следующей лекции. Составить краткий письменный конспект с выделением наиболее трудновоспринимаемых самим студентом вопросов для разбора в ходе следующего лекционного, а также практического занятия. При этом в ходе подготовки к лекциям в рамках коллектива группы с использованием рекомендуемой литературы необходимо коллективно разобрать имеющиеся непонятные вопросы и составить общий список вопросов от групп для разбора материала с помощью преподавателя на лекции. Подготовленный список вопросов оформить в печатном виде и предоставить преподавателю перед лекцией.

Описание активных и интерактивных методов обучения.

Освоение данного лекционного материала предполагает активное творческое участие студентов в выделении по описанной выше методике вопросов, которые необходимо особенно глубоко разобрать в ходе диалога с преподавателем на лекции.

Литература

1.Незлин Д.В. Радиотехнические системы: Уч. пособие. - М.:МИЭТ, 2007. - 250 с.:

ил. – С.33-37

2.Информационные технологии в радиотехнических системах: Учебное пособие / В.А. Васин, И.Б. Власов, Ю.М. Егоров и др.; Под ред. И.Б. Федорова. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. — 672 с: ил. – С.200-230

3.“Известия высших учебных заведений. Электроника” http://www.mocnit.miee.ru/redaction/.

4.http://ru.wikipedia.org/

Лекция 9 Сравнение импульсных РЛС и РЛС с непрерывным излучением

зондирующего сигнала. Структура оптимального и квазиоптимального устройств обнаружения в РЛС НИ. Построение и характеристики устройств обнаружения в импульсной и когерентно-импульсной РЛС.

План лекции:

-Cтруктурные схемы устройств обнаружения когерентных и некогерентных сигналов импульсных РЛС;

-Достоинства и недостатки РЛС с непрерывным излучением;

-РЛС НИ с немодулированной несущей и с ЛЧМ/ФМ.

Импульсные РЛС и РЛС с непрерывным излучением

Радиолокаторы с когерентными и некогерентными сигналами имеют свои достоинства и недостатки. Преимущества когерентного радиолокатора:

-высокое разрешение по частоте (по скорости радиолокационных объектов);

-более высокий энергетический потенциал из-за отсутствия потерь некогерентного накопления сигнала.

Высокое разрешение по частоте позволяет раздельно обнаруживать цели с небольшой разницей скоростей. Но еще более важна возможность подавления пассивных помех.

Основное достоинство некогерентного радиолокатора заключается в простоте устройства обработки сигналов. Структурная схема устройства обнаружения некогерентных сигналов с параллельным обзором диапазона дальностей представлена на рис.2.18.

КЛЮЧ 1		ПОРОГОВЫЙ
КЛЮЧ 1	НАКОПИТЕЛЬ	ПОРОГОВЫЙ
		КАСКАД

Строб 1

				КЛЮЧ 2
				КЛЮЧ 2		НАКОПИТЕЛЬ
Приемник
Приемник
			Строб 2		…	…
	СФ	AД
	СФ	AД

				КЛЮЧ i		НАКОПИТЕЛЬ
						НАКОПИТЕЛЬ


			Строб i		…	…
			Строб i


				КЛЮЧ N		НАКОПИТЕЛЬ
						НАКОПИТЕЛЬ


			Строб N
			Строб N

ПОРОГОВЫЙ

КАСКАД

…

ПОРОГОВЫЙ

КАСКАД

…

ПОРОГОВЫЙ

КАСКАД

Рис.2.18. Структурная схема устройства обнаружения некогерентных сигналов. СФ – согласованный фильтр, АД – амплитудный детектор.

Приемник заканчивается фильтром, согласованным с каждым импульсом пачки. После амплитудного детектора видеоимпульсы поступают на N ключей. На выходе i-го ключа образуется пачка импульсов, отраженных от цели, которая находится на дальности i ∆r . Величина ∆r представляет собой элемент обзора (разрешения) по дальности. Далее в i-м канале обнаружителя суммируются N импульсов пачки. Сумма сравнивается с порогом. По номерам каналов, в которых сработали пороговые каскады, производится оценка дальностей обнаруженных целей. Число каналов

mR =	Rmax − Rmin	,	(2.26)

	∆r

где Rmax и Rmin - границы диапазона дальностей.

Структурная схема устройства обнаружения когерентных сигналов с параллельным обзором диапазонов дальностей и скоростей целей представлена на рис.2.19.

		ГРЕБЕНЧАТЫЙ
	КЛЮЧ 1	ГРЕБЕНЧАТЫЙ
		ФИЛЬТР 1
		ФИЛЬТР 1

	СТРОБ 1
	СТРОБ 1

ПРИЕМНИК	…	ГРЕБЕНЧАТЫЙ
ПРИЕМНИК




	КЛЮЧ N
		ФИЛЬТР N


	СТРОБ N
	СТРОБ N

ПОРОГОВЫЙ КАСКАД

…

ПОРОГОВЫЙ КАСКАД

…

ПОРОГОВЫЙ КАСКАД

Рис.2.19. Структурная схема устройства обнаружения когерентных сигналов

В данном случае согласованный фильтр и детектор в приемнике не нужны. В обнаружителе производится разделение сигналов на mR дальностных каналов (так же, как на рис.2.18). Затем следуют гребенки полосовых фильтров, согласованных с пачками сигналов в каждом дальностном канале. Здесь нужны гребенки фильтров,

перекрывающие доплеровский диапазон частот fd min ÷ fd max
Число фильтров в каждой гребенке
	m	f	=	fd max − fd min	, (2.27)
	m		=		, (2.27)
				∆f
где f	d max			и fd min - границы диапазона частот Доплера; ∆f =		1	- полоса
где f				и fd min - границы диапазона частот Доплера; ∆f =		N Tсл	- полоса
						N Tсл

пропускания каждого фильтра гребенок, согласованного с когерентной пачкой.

После каждого фильтра в гребенке установлен пороговый каскад. По номеру канала дальности, в котором произошло срабатывание одного из пороговых каскадов гребенки, оценивается дальность цели. По номеру канала гребенки, в котором произошло срабатывание, определяется доплеровское смещение частоты fd . По величине fd можно определить радиальную скорость цели.

РЛС непрерывного излучения с немодулированной и модулированной несущей частотой

Радиолокаторы с непрерывным излучением (РЛС НИ) имеют ряд достоинств, делающих их использование в ряде случаев целесообразным:

-возможность получения большей (по сравнению с импульсными радиолокаторами) средней мощности передатчика при ограниченной пиковой мощности;

-наилучшие возможности селекции движущихся целей и измерения их

скоростей;

-почти нулевая величина минимальной дальности обнаружения объекта и измерения координат;

-простота РЛС в тех случаях, когда не требуется разрешать цели по дальности и измерять дальность.

Радиолокаторы с непрерывным излучением и немодулированной несущей имеют еще одно достоинство - однозначность измерения скорости цели и однозначность разрешения целей по скорости движения. Это объясняется наличием в спектре отраженного непрерывного сигнала одного пика на частоте f0 + fd , где f0 - несущая

частота, а fd - доплеровское смещение частоты. В то же время спектр когерентного импульсного сигнала включает несколько пиков примерно одного уровня.

Основным недостатком радиолокаторов с непрерывным зондирующим сигналом является попадание части зондирующего сигнала в приемный тракт. Указанный фактор может ухудшать чувствительность приемника. Этот вопрос рассматривается ниже.

С помощью радиолокаторов с непрерывным излучением можно обнаружить лишь движущиеся объекты, имеющие ненулевую составляющую скорости в направлении РЛС. Эта особенность связана с необходимостью выделять сигнал цели на фоне просачивающегося сигнала передатчика и отражений от неподвижных объектов.

Для измерения дальности объектов и разрешения их по дальности в РЛС НИ применяют частотную или фазовую модуляцию зондирующего сигнала.

Радиолокаторы рассматриваемого типа можно разделить на две группы:

-радиолокаторы с немодулированным несущим колебанием;

-радиолокаторы с частотной модуляцией или с фазовой манипуляцией.

Радиолокаторы с немодулированной несущей частотой

Начнем рассмотрение с простейшей РЛС НИ (рис.2.20), которую можно использовать для обнаружения объектов на небольших расстояниях.

Передатчик		f0	Циркулятор	f0
Передатчик			Циркулятор	f0 + f д
	f0		f0 + f д	f0 + f д
	f0		Смеситель
			Смеситель

f д

Усилитель

ФВЧ

Рис.2.20. Простейшая РЛС с непрерывным излучением. Передатчик генерирует гармонический сигнал на частоте f0 . Принятый сигнал от

движущейся цели имеет частоту f0 + f д , где f д = 2VλR . Напряжение сигнала цели после смесителя имеет частоту f д , так как в данной схеме в качестве гетеродинирующего напряжения используется часть излучаемого сигнала. Доплеровское смещение частоты чаще всего лежит в диапазоне от нескольких десятков герц до 100 килогерц. Например, при скорости движения объекта 600 м/с и длине волны 10 см

f д = 2 0600,1 =12 кГц.

Частотную характеристику усилителя доплеровских частот желательно согласовать со спектром отраженного сигнала. Если длительность отраженного сигнала ограничена величиной T0 (вследствие вращения антенны или вследствие заданного времени обнаружения объекта), то в качестве квазиоптимального можно использовать полосовой фильтр с полосой пропускания

∆f ≈ 1 .

Часто диапазон доплеровских частот

∆Fд >> ∆f .

m = ∆∆Ffд

В этом случае оптимальное решение заключается в применении гребенки из m фильтров с полосой пропускания каждого фильтра, равной ∆f . Гребенка должна перекрывать диапазон частот ∆Fd , поэтому

Сигнал с каждого фильтра гребенки детектируется и сравнивается с порогом. Номер фильтра i, на выходе которого обнаружен сигнал, дает приближенную оценку доплеровского смещения частоты

f д.i ≈ f д.min + (i −1)∆f .

Если требуется обнаруживать и сопровождать один объект, то иногда в усилителе используют следящий фильтр с полосой пропускания ∆f .

Следящий фильтр строится на базе устройства частотной или фазовой автоподстройки частоты управляемого генератора ГУН. На рис.2.21 представлена схема следящего фильтра с частотной автоподстройкой. В этой схеме частота настройки фильтра Ff постоянна и совпадает с нулем характеристики частотного дискриминатора. Сигнал с выхода усилителя преобразуется в балансном модуляторе на частоту f д + f g .

Если f д + f g ≠ F f , напряжение на выходе дискриминатора U d ≠ 0 , что приводит к

перестройке частоты ГУН вплоть до выполнения равенства f д + fg = Ff .

При этом полезный сигнал без потерь проходит через полосовой фильтр. Измерив частоту fg , можно определить доплеровское смещение по формуле

f д = Ff − fg .

		7
		f д
		Усилитель
Управляемый	fg	Балансный
генератор		модулятор
		fg + f д
		Полосовой
		фильтр
		Выход
		Частотный
		дискриминатор

Рис.2.21. Устройство со следящим фильтром.

Отличительной особенностью простейших РЛС НИ (рис.2.20 и рис.2.21) является то, что тракт приемника начинается с усилителя низкой частоты. Такое приемное устройство имеет весьма низкую чувствительность. Причиной этого является возрастание спектральной плотности шума (коэффициента шума) смесителя и усилительных каскадов на низких частотах. Изучение шумовых свойств различных электронных приборов показывает, что в области частот, меньших 1 МГц, помимо теплового и дробового шума, присутствует составляющая шума (фликкер-шум), спектральная плотность которой обратно пропорциональна частоте.

Помимо низкочастотного шума, чувствительность приемника может ухудшаться из-за наличия виброшума в радиолокаторах, расположенных на подвижных объектах. С пониженной чувствительностью приемника мирятся в тех случаях, когда не требуется большая дальность обнаружения объекта, а важнейшим параметром радиолокатора являются его габаритно-весовые характеристики. Если жертвовать чувствительностью приемника нельзя, схему усложняют, переходя к усилению сигнала на промежуточной частоте fпр (рис.2.22).

В этом случае промежуточная частота f пр

выходе гребенчатого фильтра равна f h + f di . На выходе гребенчатого фильтра (рис.2.22) постоянная частотная подставка f h опущена.

		f0			f0 + f д
		Передатчик			МШУ
Гетеродин	f г	f0	f0	− f г
Гетеродин	f г	Смеситель	f0	− f г	Смеситель
		Смеситель			Смеситель
					f г+ f д
					Усилитель

Гребенчатый фильтр

	. . .
f д.1f д.2	f д.m

Рис.2.22. Упрощенная блок-схема современной РЛС НИ.

Наиболее существенный недостаток РЛС НИ заключается в присутствии на входе приемника РЛС проникающего сигнала, который представляет собой небольшую часть зондирующего сигнала. В импульсной РЛС подобное явление также имеет место, но оно не приводит, как правило, к неприятным последствиям в связи с тем, что импульс передатчика и импульсы отраженных сигналов не совпадают во времени.

Проникающий сигнал в РЛС НИ обычно на несколько порядков превышает сигнал цели. Для характеристики величины проникающего сигнала вводят понятие развязки ν между передатчиком и приемником. Развязка определяется как отношение

мощностей зондирующего (P ) и проникающего (Pпр ) сигналов ν = Pt .

Pпр

При использовании одной антенны для излучения и приема сигналов величина ν, как правило, не превышает 30 дБ. При использовании раздельных передающей и приемной антенн развязка определяется уровнем боковых лепестков антенн, расстоянием между антеннами, а также естественными или специально установленными экранами. Величина развязки может уменьшаться из-за переотражения зондирующего сигнала местными предметами, находящимися вблизи РЛС. По данным М.Сколника [3] при использовании раздельных антенн реализуются развязки выше 80 дБ.

От основной части проникающего сигнала в приемном устройстве нетрудно избавится применяемыми способами частотной селекции. Однако ситуация осложняется тем, что зондирующий сигнал не полностью монохроматичен. Амплитуда и фаза сигнала флуктуируют вследствие наличия шумов электронных приборов, используемых в передатчике. Амплитудные и фазовые флуктуации, называемые соответственно амплитудным и фазовым шумом, вызывают расширение спектра зондирующего сигнала

(рис.2.23).

S(f)

f0 f

Рис.2.23. Спектральная плотность шума передатчика

Спектральные составляющие шума передатчика, отстоящие на fd от несущей частоты, попадают в диапазон доплеровских частот и могут создать дополнительную (к собственному шуму приемника) помеху. То же относится к фазовому шуму первого гетеродина приемника.

В [ ? ] описаны мето д и устройство уменьшения проникающего сигнала в радиолокаторах с немодулированной несущей. Метод сводится к подаче небольшой части мощности передатчика в приемник (с помощью кабеля или отдельной антенны). Поступившее в приемник напряжение вычитается из проникающего сигнала. Амплитуда и фаза поступившего напряжения регулируются таким образом, чтобы минимизировать получившуюся разность и тем самым скомпенсировать проникающий сигнал или его значительную часть.

РЛС НИ с модулированной несущей частотой

Радиолокаторы с непрерывным излучением и модулированной несущей применяют в случаях, когда необходимо измерять дальности целей и разрешать цели по

дальности. При этом весьма часто используют периодическую линейную частотную модуляцию (ЛЧМ) треугольной или пилообразной формы (рис.2.24). В некоторых случаях применяют фазовую манипуляцию (ФМ).

∆F

Рис.2.24. Треугольная (а) и пилообразная (б) частотная модуляция.

Серьезным преимуществом ЛЧМ перед ФМ в данной задаче является отсутствие необходимости в доплеровской коррекции. Это связано с гребневидной формой функции неопределенности ЛЧМ. Поэтому ограничимся рассмотрением РЛС с ЛЧМ зондирующим сигналом.

Радиолокаторы с ЛЧМ зондирующим сигналом

При использовании частотно-модулированной несущей возможны и целесообразны два вида оптимальной обработки отраженного сигнала: согласованная фильтрация или спектральный анализ. В первом случае на выходе согласованного фильтра в конце каждого периода модуляции формируется сжатый импульс. По задержке импульса

tз =	2R	(2.28)
	c

можно определить дальность цели.

Рассмотрим вторую возможность на примере использования ЛЧМ треугольной формы. Для этого обратимся к рис.2.25 и рис.2.26. На рис.2.25 представлена упрощенная блок-схема радиолокатора. Передатчик излучает сигнал с текущей частотой f п. Вначале рассмотрим прием сигнала, отразившегося от неподвижной цели ( fd = 0 ). Отраженный от цели сигнал в этом случае имеет такой же закон изменения частоты, как и зондирующий, задержанный на величину tз

f отр(t) = f п(t − t з).

Передатчик

Цель

Приемник

СМ

f п − f отр

Анализатор

спектра Выход

Рис.2.25. Упрощенная блок-схема РЛС НИ с частотной модуляцией. Преобразованный сигнал на выходе смесителя с частотой

f dif (t) = f п(t) − f отр(t)

поступает на анализатор спектра, на выходе которого формируется оценка дальности цели R. Временные зависимости частот f п, f отр и f dif представлены на рис.2.26. На

временной диаграмме преобразованного сигнала (рис.2.26, б) знаками + и – отмечены соседние половинки периода модуляции. Это сделано для того, чтобы подчеркнуть противоположные изменения фазы на этих интервалах времени. Знак + соответствует нарастанию фазового сдвига, знак – соответствует уменьшению фазового сдвига. Заметим, что фазовый сдвиг на некотором интервале времени равен интегралу от частоты сигнала. Площади трапеций, отмеченных знаками + и – на рис.2.26, одинаковы. Следовательно, фазовые сдвиги на этих участках одинаковы по абсолютной величине.

f		Tm
f п	f dif		∆F
	f dif		∆F
f отр			t
t з			t
t з		a)
		a)
fdif
		b)	t
		b)

Рис.2.26. Временные диаграммы при fд = 0.

а) Частота передатчика (сплошная кривая)

и частота отраженного сигнала (штриховая кривая); б) Частота преобразованного сигнала.

Поскольку набеги фаз имеют противоположные знаки, фазы преобразованного сигнала в начале и конце периода Tm одинаковы. Такой сигнал является периодическим

с когерентностью 2-го рода. Следовательно, спектр этого сигнала дискретный.
Спектральные составляющие располагаются на частотах, кратных F =					1	.

				m	Tm

На большей части периода модуляции Tm			частота f dif	сохраняет постоянное
значение
f dif =	∆F	t	з		(2.29)

	T

В (2.29) T = T2m . Объединяя формулы (2.28) и (1.29), получим выражение для дальности цели

R = f dif	cT	.	(2.30)

	2∆F

Следовательно, для определения дальности цели достаточно измерить частоту f dif преобразованного сигнала.

Для оценки величины f dif рассчитаем спектр преобразованного сигнала. При этом несколько упростим задачу, полагая, что f dif всюду выражается формулой (2.29).

При fd = 0 спектры периодических импульсных последовательностей, отмеченных знаками + и –, одинаковы. Рассчитаем спектр первой из этих последовательностей. Форма огибающей спектра, совпадает со спектром одного импульса S1(ω)

	sin(		ω −	ωdif		T )
	sin(			2		T )
S1(ω) =UT				2			.	(2.31)
S1(ω) =UT		ω − ωdif			T		.	(2.31)
			2		T
			2
В (2.31) U - амплитуда импульса,		ωdif		= 2π f dif

iωm , где ωm = 2πFm , для получения спектра импульсной

последовательности нужно в (2.31) сделать замену ω= iωm . Тогда выражение искомого

спектра будет иметь вид

(iω

) =UT sin((ωdif − iωm ) 2)

(2.32)

(ωdif

− iωm ) 2

Если

ωdif

- целое число, то максимум спектра имеет место при

i =

ωdif

и его

ωm

величина равна

Smax =UT .

Амплитуды

соседних

(по

отношению к

максимальной)

составляющих определяются подстановкой в (2.32) значения

i = ωdif ±1.

ωm

Следовательно, S(ωdif ± ωm ) =

2UT

= π Smax

Амплитуды следующей пары спектральных составляющих, имеющих номера

i =

ωdif

± 2, равны нулю. Полученные результаты иллюстрируются на рис.2.27, а.

ωm

Smax

ωdif

dif

ωm

−1

ωm

ωm + 2

ωdif

ωm

Рис.2.27. Спектр преобразованного сигнала

а) ωdif

- целое число, б) ωdif - нецелое число.

ωm

Таким образом, основной лепесток спектра преобразованного сигнала содержит небольшое число (в данном примере три) спектральных составляющих. Среди них не трудно выделить максимальную, частота которой iωm = ωdif или ifm = f dif .

Более типичная ситуация имеет место, когда ωdif не является целым числом. В

ωm

этих случаях номер наибольшей составляющей спектра определяется соотношением

i − ωdif ≤ 0,5 .

ωm

Данная ситуация иллюстрируется на рис.2.27, б.

Отметим характерную особенность рассматриваемого спектра: при изменении дальности цели величина ωdif изменяется непрерывно. Вместе с ωdif изменяет свое

положение огибающая спектра. При этом положения спектральных составляющих не изменяются, но изменяются их амплитуды. Частота f dif , характеризующая дальность

цели, измеряется с ошибкой δ f dif , которая не превышает 0,5Fm .

Используя (2.32), найдем максимальную ошибку измерения дальности цели

	cT		c
δRmax =		δ f dif .max =		.	(2.33)
	2∆F		8∆F

Оценим разрешающую способность по дальности. При сближении двух целей их сигналы еще воспринимаются раздельно, если максимумы их спектров разнесены на величину ∆f ≥ 2 fm . Действительно, если ∆f = fm , невозможно определить, принадлежит

ли сигнал с таким спектром одной цели или двум целим. Подставив в (2.33) вместо

δ f dif требуемую разность частот для двух целей (∆f								= 2 fm ), получим разрешающую
способность ∆R
∆R =	c	2 f		T	=	c	.
			m ∆F			2∆F
2
Рассмотрим теперь общий случай обработки сигнала, отраженного движущейся
целью. При		f д ≠ 0
f dif .1= f dif		− f д,			а	во втором - f dif .2 = f dif		+ f д. Здесь f dif - частота

преобразованного сигнала при f д = 0. Как следствие, составляющие спектра на интервалах "+" смещаются влево на fd , а на интервалах "–" - на такую же величину вправо. Частоту f dif , необходимую для измерения дальности цели, можно рассчитать по формуле

f = f dif .1+ f dif .2 . dif 2

f п

f отр

f д

fdif.2

fdif.1

b) t

Рис.2.28. Временные зависимости частот; а) Частоты передатчика (сплошная кривая) и отраженного сигнала (штриховая

кривая); б) частота преобразованного сигнала.

Если требуется измерять скорость цели, то значение f д рассчитывается по формуле

f д =	f dif .2 − f dif .1	.
	2

Для того, чтобы располагать значениями f dif .1 и f dif .2, нужно иметь

двухканальное устройство для раздельной обработки преобразованных сигналов, отмеченных знаками "+" и "–". Реализация такого устройства не вызывает затруднений.

Задание на самостоятельную проработку

Описание активных и интерактивных методов обучения.

Литература

1.Незлин Д.В. Радиотехнические системы: Уч. пособие. - М.:МИЭТ, 2007. - 250 с.:

ил. – С.74-79

3.“Известия высших учебных заведений. Электроника” http://www.mocnit.miee.ru/redaction/.

4.http://ru.wikipedia.org/

Лекция 10 Структура цифровой следящей системы первого порядка. Передаточная

функция, частотная и импульсная характеристики. Условие устойчивости. Переходные процессы в следящей системе первого порядка.

План лекции:

-Структура следящих измерителей;

-Метод максимума;

-Дифференциальный метод;

-Цифровые следящие устройства;

-ЦСС с астатизмом первого порядка.

Следящие измерители координат цели

Устройства сопровождения цели по угловым координатам, дальности и скорости предназначены для измерения координат, устранения помеховых отражений от нежелательных объектов и частичного уменьшения шума приемника. Такие устройства обычно выполняются в виде следящих систем с астатизмом первого, второго или третьего порядка. Координаты объекта связаны с параметрами отраженного сигнала. Дальность цели - с временной задержкой сигнала, скорость - с доплеровским смещением частоты, угловые координаты - с положением фазового фронта сигнала. Поэтому будем использовать как синонимы термины "следящий измеритель координат цели" и "следящий измеритель параметров сигнала"

Следящие измерители могут быть выполнены в виде аналоговых или цифровых устройств. В современной аппаратуре значительно чаще используются цифровые устройства. Поэтому ограничимся рассмотрением устройств этого типа.

Структура следящих измерителей На входе следящего измерителя присутствует сигнал, являющийся функцией

времени и значения измеряемого параметра, который обозначим в общем виде буквой

α0

U c (t,α0 ) .

В измерителе формируется опорный объект (опорное напряжение или число), сходный с сигналом и содержащий оценку параметра, которую обозначим α. Следящий измеритель состоит из двух блоков: дискриминатора и управляющего устройства (рис.2.29). В первом из блоков оценка α сравнивается со значением параметра α0 и

величина, пропорциональная их разности (рассогласованию)

U д= K д ∆α = K д(α0 − α) ,

поступает на вход управляющего устройства. В этом устройстве под действием рассогласования формируется коррекция α. Коррекция оценки α продолжается до тех пор, пока (в идеале) оценка не сравняется с истинным значением параметра α0 .

U c (t,α	0	)
			Дискриминатор	УУ

U оп(α)

Рис.2.29. Блок - схема следящего измерителя. УУ - управляющее устройство.

Дискриминатор содержит в простейшем случае коррелятор, на входы которого поступают принятый сигнал и опорное напряжение. Очевидно, что максимум выходного напряжения коррелятора U kop имеет место при α = α0 .

Измерение α0 методом максимума не эффективно по двум причинам. Во-первых, нередко зависимость U cor (α0 −α) имеет почти плоскую вершину (рис.2.30, а), что

объясняет низкую чувствительность к рассогласованию. Во-вторых, имея одно значение U kop , нельзя решить, в какую сторону нужно изменять α, чтобы приближаться к α0 .

Поэтому обычно используют дифференциальный метод.

Uкор(α0 − α)

0	α0 − α
a)
Uкор(α0 − α +δα)	Uкор(α0 − α −δα)

−	δα 0 δ	α	α0 − α

	b)

Рис.2.30. Иллюстрация принципа работы следящего измерителя Берутся (последовательно или одновременно) два значения корреляционного

интеграла; первое - при опорном напряжении U оп(α + δα) , второе - при U оп(α − δα) . На выходе дискриминатора образуется разность U кор(α0 − α − δα) −U кор(α0 − α + δα) .

Методика иллюстрируется на рис.2.30, б.

Из рассмотрения рис.2.30, б следует, что при U кор (α0 − α − δα) =U кор (α0 − α + δα) ,

α = α0 .
	В	случае			U кор (α	0	− α − δα) <U кор (α		0	− α + δα) , α > α0 , а при
						0			0
U кор (α	0	− α − δα) >U кор (α		0	− α + δα) , α < α0 .
	0			0
	Нетрудно придти к выводу, что зависимость выходного напряжения
дискриминатора от			рассогласования					U д(α0 − α) ,		называемая дискриминационной

характеристикой, имеет вид, показанный на рис.2.31.

Uд(α0 − α)

0 α0 − α

Рис.2.31. Дискриминационная характеристика.

Ввиду малости постоянной времени дискриминатора этот элемент обычно

считают безынерционным.

В качестве его коэффициента передачи K д принимают

производную дискриминационной характеристики в точке α = α0 . Размерность

K д

в аналоговых устройствах или

K д

ед

в цифровых устройствах.

Заметим, что для одновременного сравнения выходных напряжений корреляторов

U кор (α

− α − δα) и U кор (α

− α + δα) нужно использовать два коррелятора с опорными

напряжениями U оп(α + δα) и U оп(α − δα) соответственно.

Управляющее устройство состоит из интегрирующих звеньев и преобразователя. Последний необходим для преобразования напряжения (числа) на выходе интегратора в значение оценки параметра α. Преобразователь тоже обычно считают безынерционным

элементом с коэффициентом передачи Кпр. Размерность							α	в аналоговых
					K пр	:	α
					K пр	:	В
устройствах или	K пр	:	α	в цифровых.			В


			ед
			ед

Цифровые следящие устройства

Дискриминатор обычно строится по одному из двух возможных вариантов. В первом случае используется аналоговый дискриминатор, выходное напряжение которого подвергается аналого-цифровому преобразованию. Во втором варианте входное воздействие оцифровывается, а операция вычитания

∆α~ = α~ 0 − α~

осуществляется в цифровом устройстве.

В соответствии с принятым вариантом дискриминатора преобразователь выдает значение α в аналоговом или цифровом виде. Если преобразователь является

аналоговым элементом, между ним и интегратором устанавливается цифро-аналоговый преобразователь (ЦАП).

Масштабирующее звено с коэффициентом передачи m является линейным безынерционным звеном. Цифровой интегратор обычно выполняется как накапливающий сумматор (рис.2.32).

Uвх	+	Uвых.1

Регистр

Uвых.2 Синхроимпульсы

Рис.2.32. Схема цифрового интегратора

В качестве выходного числа можно использовать выход сумматора	~	или
	Uвых.1

выход регистра Uвых.2 . Волнистая черта над символом U придает ему смысл числа.

Период тактовых импульсов обозначим

Ti .

Определим передаточную функцию

интегратора при использовании Uвых.1

. Разностное уравнение для Uвых.1 имеет вид

(2.34)

U вых.1(n)

=U вх (n)

+ U вых.1(n −1) .

Переходя к z - преобразованиям обеих частей равенства, получим

(z)z

−1

U вых.1(z) =U вх (z) + U вых.1

Отсюда передаточная функция интегратора равна

H i1(z) =

U вых.1(z)

(2.35)

U вх (z)

z −1

При использовании второго выхода интегратора

U вых.2 (z) =U вых.1(z)z −1.

Следовательно, передаточная функция интегратора в этом случае равна

Hi2 (z) =

(2.36)

z −1

Структурная схема цифровой следящей системы с астатизмом первого порядка представлена на рис.2.33.

U (α0 )	Цифровой	× m	+
	дискриминатор	× m
	дискриминатор
	U (α)	Преобразователь	Регистр
		Kпр	Ti

Рис.2.33. Структурная схема следящей системы первого порядка Как видно из рисунка, здесь используется второй выход интегратора. В данном

случае это необходимо, так как момент передачи очередного числа на вход и реакция следящей системы должны быть разделены одним тактовым интервалом. В противном случае состояние системы (число на выходе) будет неопределенным.

Запишем очевидное выражение для передаточной функции разомкнутой системы:

H (z) раз = K дm z 1−1K пр = zK−01,

где K0 = K дm K пр.

Определим размерность величины K0 . Поскольку m - безразмерный множитель,

K0 = K д K пр = едα едα ,

то есть K0 - безразмерная величина.

Найдем выражение передаточной функции замкнутой следящей системы (по

выходу преобразователя):

H (z) =

H (z) раз

(z −1)

. (2.37)

1+ H

(z)

1+ K

(z −1)

z −1+

раз

Таким образом, K0

является единственным параметром передаточной функции. С

помощью выражения (2.37) легко определить область значений K0 , внутри которой следящая система устойчива. Действительно, единственный полюс H (z)1 равен

z1 =1− K0 .

Поскольку для устойчивости системы необходимо и достаточно выполнить условие

z1 <1,

получаем

1− K0 <1.

Из последнего неравенства следует

0 < K0 < 2 .

Как далее будет показано, часто целесообразно для определения K0 использовать более жесткое соотношение:

0 < K0 <1.

Определим теперь нормированную частотную характеристику системы первого

порядка . Для этого в выражении (2.48) переменную z нужно заменить на

exp j ωн.

Тогда получим

K(ωн) =

exp j ω

+ K

−1

cos ω

+ K

−

1+ j sin ω

Амплитудно-частотная характеристика системы равна

K(ωн) =

(2.38)

(cos ω

+ K

−1)2 + sin 2 ω

1+ (1− K

− 2(1− K

)cos ω

Проанализируем полученную АЧХ. При

ωн = 0 K(0) = 1. При ωн = π

K (π) =

2 − K0

При K0 =1 K (ωн) =1,

т.е.

следящая система не фильтрует входное воздействие,

что в большинстве случаев неприемлемо.

Полосу пропускания следящей системы ∆ωн по уровню –3 дБ определим из выражения

K 2

K 2 (ωн) = 1+ (1− K0 )2 − 2(01− K0 ) cos ∆ωн = 0,5.

В результате несложных преобразований получим

	0,5K
		0
∆ωн = 2arcsin		0		.

	1− K
	1− K		0
			0

Если K0 ≤ 0,7, то

0,5K

arcsin

≈

1− K0

1−

∆ωн ≈

;

∆ω =

∆ωн

(2.39)

− K

T и

1− K

В формуле (2.39) T и есть период импульсов, тактирующих интегратор.

На рис.2.34 приведены рассчитанные по формуле (2.38) АЧХ цифровой следящей системы для нескольких значений K0 . Как следует из рисунка и формулы (2.39), с уменьшением K0 и (или) увеличением T и полоса пропускания системы уменьшается.

Рис.2.34. Амплитудно - частотные характеристики следящего измерителя первого порядка

Заметим, что дисперсия ошибки слежения, обусловленной помехами, сопровождающими полезный сигнал, определяется выражением

σ2 = a ∆ω

Pc Pш .

Здесь a - коэффициент пропорциональности; Pc Pш - отношение мощностей сигнала и помехи на входе следящей системы.

Найдем теперь выражение для импульсной характеристики следящей системы первого порядка. Передаточная функция линейной системы равна Z- преобразованию

импульсной характеристики. Следовательно, импульсная характеристика следящей системы равна обратному Z-преобразованию ее передаточной функции. Расчет импульсной характеристики системы первого порядка очень прост. Выполнив обратное Z-преобразование функции (2.37), получим

h(n) =	0	при	n = 0,
		(1− K0 )n −1 при	n ≥1.	(2.40)
	K0
Используя равенство (2.40), можно рассчитывать реакцию следящей системы на
то или иное входное воздействие с помощью дискретной свертки:
n	u(n − i )вхh(i)
u(n)вых = ∑
i =1		.

Нижний предел суммирования равен единице, так как h(0) = 0. В частности, подставив в это выражение u(n – i) = 1, найдем реакцию системы первого порядка на единичную ступеньку (переходный процесс):

(1− K

)i −1

=1− (1− K

uвых

∑

i =1

Определим

длительность переходного процесса n.1 как интервал

времени (в

числе тактовых импульсов)

до достижения выходной величиной значения

uвых = 0,9.

Тогда

n.1= −

lg(1− K0 )

(2.41)

В таблице 2.2 представлены округленные значения n.1 в функции коэффициента

передачи разомкнутой петли K0 .

Таблица 2.2. Округленные значения n.1 в функции коэффициента усиления разомкнутой петли K0.

K0	0.2	0.3	.4	.5	0.6	0.7	0.8

n.1	10	6	5	3	2	2	1

Задание на самостоятельную проработку

Описание активных и интерактивных методов обучения.

Литература

1.Незлин Д.В. Радиотехнические системы: Уч. пособие. - М.:МИЭТ, 2007. - 250 с.:

ил. – С.75-78

3.“Известия высших учебных заведений. Электроника” http://www.mocnit.miee.ru/redaction/.

4.http://ru.wikipedia.org/

Лекция 11 Система второго порядка, ее передаточная функция и частотная

характеристика. Условия устойчивости.

План лекции:

-Цифровые следящие системы с астатизмом второго порядка;

-Структурные схемы следящего измерителя второго порядка;

-Схема цифрового интегратора с коррекцией.

-Шумовые ошибки;

-Динамические ошибки цифровых устройств сопровождения цели;

-Флуктуационные погрешности, угловые погрешности

Цифровая следящая система с астатизмом второго порядка

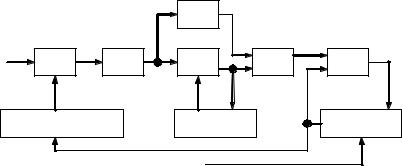
Структурная схема системы второго порядка приведена на рис.2.35. В соответствии с определением система включает в себя два интегрирующих звена. Одно из них (в данном случае первое), как и в аналоговом устройстве, содержит корректирующую цепь для придания устойчивости системе. Этим звеном схема на рис.2.35 отличается от схемы следящей системы первого порядка.

			x M
U вх	K д
U вх	–	x m	+	+	+
	–	x m	+	+	+
U вых
Преобразователь			Регистр		Регистр

T и

Рис.2.35. Структурная схема следящего измерителя второго порядка Цель включения корректирующей цепи - обеспечить прохождение входного

числа на выход интегратора. Эта цепь состоит из линейного безынерционного звена с коэффициентом передачи M. Схема интегратора с корректирующей цепью представлена отдельно на рис.2.36.

x M
вход		выход
+	+	выход
РЕГИСТР

Рис. 2.36. Схема цифрового интегратора с коррекцией Передаточная функция собственно интегратора (без корректирующей цепи)

определяется формулой (2.35). Передаточная функция интегратора вместе с корректирующей цепью равна

H (z)	кор	=	z		+ M =	z(1 + M ) − M	.
	кор		z −1			z −1

Следовательно, передаточная функция разомкнутой следящей системы выражается следующим образом:

H (z)	раз 2	= H (z)	раз1	H (z)	кор	=	K0 [z(1 + M ) − M ]	.

							(z −1)2

Значит, передаточная функция замкнутой следящей системы второго порядка по выходу преобразователя запишется в виде

[z(1 + M ) − M ]

H (z)2

(z −1)2

= K0

z(1 + M ) − M

(2.42)

K0 [z(1 + M ) − M ]

(z −1)2 + K

(1 + M )z − K

(z −1)2

Ограничения на параметры следящей системы, исходя из требования

устойчивости ее, приведем без вывода:

K0 > 0 , M > 0 ,

K0 (1 + 2M ) < 4.

Подставив в

выражение

(2.42)

z = exp j ωн,

найдем комплексную

частотную

характеристику системы. Ее модуль даст АЧХ следящей системы:

K (ωн) = K

2 + 2M +1 − 2(M 2 + M )cos ωн

(2.43)

1 + a2 + b2 + 2a(1 + b)cos ωн + 2b cos 2ωн

В формуле (2.43) приняты следующие обозначения

a = K0 (1 + M ) − 2; b =1 − K0 M .

Анализ соотношения (2.43) показывает, что, если M = 0 (коррекция отсутствует), всегда найдется некоторое критическое значение частоты ωн.кр, при котором следящая система оказывается неустойчивой. Критическое значение ωн.кр, определяемое путем приравнивания нулю знаменателя в выражении (2.43), равно

			ωн.кр = arccos(1 − 0,5K0 ).	(2.44)
В качестве примеров на рис.2.37 приведены зависимости				K (ω) для следующих
значений параметров следящей системы:
K0 > 0 ,		M =1	(кривая 1);
K0	> 0,5,	M =1	(кривая 2);
K0	> 0,2,	M =1	(кривая 3);
K0	> 0,2,	M = 0,5 (кривая 4);
K0	> 0,5,	M = 0 (кривая 5).

Рис.2.37. Амплитудно - частотные характеристики следящего измерителя второго порядка.

Для приближенной оценки полосы пропускания системы второго порядка по уровню –3 дБ можно воспользоваться соотношением:

∆ω ≈	1,3πK0	;	∆f ≈	0.65K0	. (2.56)
	T и			T и

Динамические ошибки цифровых устройств сопровождения цели.

В работе следящей системы различают переходный процесс и установившийся режим. Аппроксимируем закон изменения измеряемого параметра сигнала полиномом

L
α0 (t) = ∑al t l ,	(2.51)

l = 0

где L - порядок старшей производной измеряемого параметра сигнала, отличной от нуля.

Если на интервале времени, превышающем длительность переходного процесса (например, (2.41) для системы первого порядка), все коэффициенты al неизменны, то имеет место установившийся режим. Переходный процесс возникает в момент включения системы или при изменении коэффициентов al в (2.51). Погрешности в течение переходного процесса могут быть весьма большими. Их продолжительность уменьшается с увеличением коэффициента передачи разомкнутой петли следящей системы.

Динамические погрешности цифровой следящей системы в установившемся режиме можно рассчитать по формуле.

		L	S		dl α0(t)
∆	д	= ∑		l
					dtl
		l = 0
Таким образом, ∆д является взвешенной суммой производных α0 (t)
коэффициенты (коэффициенты ошибки)			Sl		определяются выражением

(2.52)

. Весовые

			T l	dl H
			T l	dl H		(z)
S	l	=	и		∆
S		=	l!	dzl			z =1	(2.53)
			l!	dzl

Здесь H ∆ (z) - передаточная функция по ошибке для цифровой системы

H ∆ (z) =1 − H (z).

Рассчитаем коэффициенты статической (для неподвижного объекта) и динамических ошибок для следящих систем с астатизмом первого и второго порядка.

Для системы первого порядка

H∆(z) =1	−	k0	=	z −1
		z −1 + k0		z −1 + k0 .

Коэффициент статической ошибки равен

S0 = H∆(z) z =1 = 0 ,

т.е. статическая ошибка отсутствует. Коэффициент ошибки S1 равен

z −1

Tи

S =T

и dz z −1 + k

z =1

Следовательно, при наличии только первой производной функции α0 (t) динамическая ошибка равна

∆д = Tи dα0(t) k0 dt .

Для системы второго порядка

H∆(z) =1 − H (z) =

(z −1)2

(z −1)2 + k0 (1 + M )z − k0M

Статическая ошибка равна нулю, поскольку S0 = 0 .

Нетрудно убедиться в том, что

S1 = 0 ,

т.е. при наличии только первой

производной отслеживаемого параметра сигнала динамическая ошибка отсутствует.

Коэффициент S2 равен

T 2 d

∆

(z)

T 2

dz2

z =1

Следовательно, при наличии второй производной отслеживаемого параметра сигнала

	T 2	d 2α	0	(t)
∆д =	и		0		.
∆д =	k0	dt 2			.
	k0	dt 2

В общем случае, если порядок системы больше, чем порядок некоторой производной функции α0 (t)

отсутствует. Используя это положение, можно выбирать порядок системы, ориентируясь на производную функции α0 (t), имеющую наибольшую величину.

Флуктуационные погрешности

В разделе упоминалось о флуктуациях радиолокационного центра цели. В [1.4.3] приведены формулы для оценки средних квадратических отклонений центра цели от его среднего положения

σц ≈ 0, 35 · Lц ,

(2.54)

где Lц – максимальный размер цели вдоль той или иной координаты. Средняя квадратическая величина флуктуаций центра цели вдоль координаты «дальность» σR выражается формулой (1.4.26), если в нее подставить длину цели вдоль данной координаты. Для оценки среднего квадратического значения угловых флуктуаций (в радианах) нужно воспользоваться формулой

	σβ	= 0.35	L2	,			(2.55)
	σβ	= 0.35	R	,			(2.55)
			R
где L2	- длина цели в поперечном направлении, а R - дальность цели.
Среднее квадратическое значение флуктуаций доплеровского смещения частоты
определяется по формуле
	σ f	≈ 0,35.	2L	2 dβ		.	(2.56)
	σ f	≈ 0,35.	λ		dt	.	(2.56)
			λ		dt
В (2.56)	β – ракурс цели (в радианах), λ – длина волны.
Благодаря	фильтрующему действию следящих измерителей, ошибки измерения

параметров сигнала меньше, чем σR,, σβ, σf. .Для вычисления погрешностей измерения ФЫнужно проинтегрировать произведение спектральной плотности флуктуаций радиолокационного центра цели S(ω) и квадрата частотной характеристики измерителя k(ω). S(ω) является убывающей функцией частоты. Если коэффициент корреляции флуктуаций аппроксимировать экспоненциальной функцией, то придем к выражению S(ω) в виде

S(ω) =	S(0)			(2.57)
		ω 2
1	+
		ωa	2

В (2.57) S(0) = 4.σc2.ωa

; ωa =

τк

Дисперсия флуктуационной ошибки определяется формулой

∞

2 =

∫ S(ω).k 2(ω).dω

(2.58)

2π

В частности, для следящего измерителя первого порядка

∞

S(0)

dω

σ2 =

∫

σc k

(2.59)

2π

0 1

k + ω

ωa2

В формуле

(2.59)

величина

“к”-

коэффициент передачи разомкнутой петли

следящей системы.

При угловом

сопровождении низколетящего объекта в состав сложной цели

входят истинный объект и его антипод (глава 1). Расстояние между объектом и антиподом значительно превышает размер объекта. Поэтому дисперсия ошибки слежения по углу места может быть весьма большой, что нередко приводит к срыву сопровождения. Иногда в подобных ситуациях отказываются от автоматического слежения по углу места. Приближенную оценку этой координаты осуществляют по выходному напряжению соответствующего дискриминатора.

Угловая погрешность сопровождения цели в РЛС с коническим сканированием из-за флуктуаций амплитуды сигнала цели.

Для расчета дисперсии	2	указанной погрешности можно использовать
Для расчета дисперсии	σa	указанной погрешности можно использовать
формулу [1.4.5]

σ2 = θ2 ∆f . (2.60) a 4π2 f ск2 τк

В(2.60) θ - ширина диаграммы направленности антенны, f sc - частота

сканирования, Δf– полоса пропускания следящего измерителя, τк - интервал корреляции амплитудных флуктуаций

Задание на самостоятельную проработку

Описание активных и интерактивных методов обучения.

Литература

1.Незлин Д.В. Радиотехнические системы: Уч. пособие. - М.:МИЭТ, 2007. - 250

с.: ил. – С.75-78

3.“Известия высших учебных заведений. Электроника” http://www.mocnit.miee.ru/redaction/.

4.http://ru.wikipedia.org/

Лекция 12 Устройства сопровождения цели.

План лекции:

-Устройства углового сопровождения цели

-Моноимпульсный радиолокатор на базе ФАР

-Угломер с квадратным сканированием

-Следящий измеритель дальности.

Устройства углового сопровождения цели

Для реализации дифференциального метода углового сопровождения цели (измерения угла) в одной плоскости нужно иметь два приемных антенных луча (1 и 2), несколько сдвинутых один относительно другого (рис.2.38, a), или один луч, поочередно

устанавливаемый в положения 1 и 2 с частотой сканирования f ск (рис.2.38, б). В первом случае реализуется дискриминатор с одновременным сравнением сигналов, во втором - дискриминатор с последовательным сравнением сигналов. В канале измерения производится одновременное или последовательное сравнение амплитуд сигналов, принятых по двум лучам.

Цель

РСЛ

Цель

РСЛ

б)

Рис.2.38. Иллюстрация дифференциального метода измерения углового положения объекта.

Прямая, проходящая через точку пересечения двух диаграмм направленности (ДН), называется равносигнальным направлением (РСН) или равносигнальной линией (РСЛ). Если источник сигнала находится на РСЛ, то сигналы, принятые по двум лучам, одинаковы. В случае смещения источника сигнала с РСЛ амплитуды (или фазы) принятых по двум лучам сигналов различаются. При одновременном сравнении сигналов их разность пропорциональна смещению источника сигнала с РСЛ. При последовательном сравнении смещение источника сигнала с РСЛ приводит к амплитудной модуляции напряжения на выходе антенны с частотой, равной частоте коммутации луча ( f ск).

С помощью устройства управления диаграмма направленности антенны поворачивается до тех пор, пока источник сигнала не окажется на РСЛ. Признаком этой ситуации является нулевое значение разности двух принятых сигналов при их одновременном сравнении. При последовательном сравнении подобным признаком является отсутствие амплитудной модуляции принятого сигнала с частотой f ск.

Рассмотрим наиболее употребительные разновидности угломерных устройств. Первое из них представляет класс устройств с одновременным сравнением сигналов. Такие устройства называют моноимпульсными. Остальные устройства относятся к классу устройств с последовательным сравнением сигналов.

Суммарно-разностное моноимпульсное устройство с фазовым сравнением сигналов

Принцип работы моноимпульсных измерителей рассмотрим на примере устройства с зеркальными антеннами. Затем отметим особенности использования фазированных антенных решеток (ФАР). На рис.2.39, a схематически представлена моноимпульсная антенна, предназначенная для измерения одной угловой координаты цели β (в плоскости рисунка). Антенна состоит из двух элементов, их фазовые центры обозначены цифрами 1 и 2. Кроме того, СВЧ часть устройства содержит суммарноразностную схему, обозначенную символами "+" и "-", и фазовращатель,

осуществляющий фазовый сдвиг π2 .

					Цель1
		V1	1
	LA l		A	β	B
	LA l				Цель2
					Цель2
		V2	2
			V1
			π 2	U с	U р
			V2
			a)
			V1
			U р
			ϕ	U с
				U с
			V2
			б
	Рис.2.39. Суммарно – разностный метод измерения
углового	положения		цели	в	одной	плоскости
a) элементы	антенны	и	суммарно	–	разностное	устройство;

b) векторная диаграмма

Если цель 1 находится на оси антенны АB, то длины путей сигнала до фазовых центров 1 и 2 одинаковы. Следовательно, одинаковы фазы принятых сигналов. Амплитуды сигналов V1 и V2 тоже одинаковы, так как оси ДН антенн параллельны.

Следовательно, разность V1 и V2	(разностный сигнал) U	dif	= 0 .
		dif
Из этого, кстати, следует, что ось антенны АВ			является равносигнальной
линией. Суммарный сигнал
	U c =V1 +V2 = 2V1 .

Если направление на цель 2 составляет угол β с РСЛ, то разность фаз сигналов V1 и V2 равна

ϕ =

2π sin β .

При этом амплитуды и фазы U sum

и U dif

можно найти с помощью векторной

диаграммы на рис.2.39, б

U c

= 2

V 1

cos

ϕ ;

U p

= 2

V 1

sin ϕ ;

(

U dif

)

= π или

− π в зависимости от

U sum

знака ошибки β. После фазовращателя на

π векторы U sum и U dif оказываются в фазе

или в противофазе в зависимости от знака β.

Объединяя

полученные

формулы

для

U c

U dif ,

получим выражение,

связывающее их амплитуды,

U р =U с tg

π sin β

=U с tg

Для малых угловых ошибок

sin β ≈ β и tg

π sin β

≈

π β

Отсюда

U p ≈U c

π β

=U c

πLβ

≈ µ U c β

(2.60)

2λ

Вформуле (2.60) µ = 2πθ ≈ 1,θ57 . Здесь θ- ширина ДН антенны, образуемой обоими

ееэлементами. Величина θ выражается в тех же единицах, что и ошибка β (в градусах или радианах).

Часто приходится измерять две угловые координаты цели в двух взаимно перпендикулярных плоскостях, поэтому приемная антенна включает в себя четыре элемента, попарно разнесенные в двух ортогональных плоскостях. Фазовые центры этих

элементов (1, 2, 3, 4) и схема получения суммарного U c и двух разностных напряжений U dif .1 и U p.2 показаны на рис.2.40.

–

1 3+

13+

24+

Uр.2

– Uр.1

π2 Uс

Рис.2.40. Устройство фазового сравнения сигналов в двух плоскостях. Амплитуды U c , U dif .1, U p.2 просто выражаются через напряжения на выходах

элементов антенны V1 ÷V4 :

U c =U1 +U 2 +U3 +U 4 ,
U p.1=U1 +U 3− (U 2 +U 4 ) = µ U c β1,	(2.61)
U p.2 =U1 +U 2 − (U3 +U 4 ) = µ U c β2.

Здесь β1 и β2 - компоненты угловой ошибки в двух взаимно перпендикулярных

плоскостях.

На рис.2.41 представлена структурная схема приемника моноимпульсной РЛС, содержащая три канала.

Uс	Усилитель	АРУ

Uр.1	Усилитель	Фазовый
		детектор

Uр.2	Усилитель	Фазовый
		детектор

УПТ

К приводам антенны

Рис.2.41. Блок - схема приемника моноимпульсной РЛС.

Выходы фазовых детекторов являются выходами двух дискриминаторов устройств, измеряющих две угловые координаты цели. Величина U sum в формулах (2.61) может изменяться на несколько порядков из-за изменения дальности цели и ее ЭПР. Чтобы крутизна дискриминационной характеристики не зависела от амплитуды

суммарного сигнала, в приемнике используется автоматическая регулировка усиления (АРУ). АРУ является общей для всех трех каналов и работает по напряжению суммарного сигнала.

Несколько упрощая ситуацию, будем считать, что АРУ поддерживает амплитуду напряжения на выходе канала суммарного сигнала равной U 0 . Кроме того, будем полагать, что все три канала идентичны, т.е. коэффициенты усиления во всех каналах одинаковы. При этом амплитуды выходных напряжений каналов равны:

U с.вых =U0 ;

U р.1.вых = µ U0 β1;	U р2.вых = µ U0 β2.
Управляющие устройства следящих	измерителей состоят из усилителей

постоянного тока (УПТ) и приводов антенны в двух ортогональных плоскостях. Действием последних рассогласования β1 и β2 сводятся к нулю, и угловое положение цели определяется направлением РСЛ. Рассмотренный измеритель имеет астатизм 1-го порядка; функции интеграторов выполняют приводы антенны. Коэффициент передачи разомкнутой петли измерителя равен

K1 = K d K упт K прив = K д µ U0 K упт K прив . (2.62)

Здесь K д= K фдµU 0 - коэффициент передачи дискриминатора, K фд -

коэффициент передачи фазового детектора. Остальные коэффициенты передачи не нуждаются в расшифровке.

Если в процессе работы устройства коэффициенты усиления приемных трактов

изменятся, может	измениться и коэффициент передачи следящего измерителя.
Предположим, что	коэффициент усиления разностного канала изменился на ∆ K р, а

коэффициент усиления суммарного канала изменился на ∆ K с ( ∆K сand ∆K р - не-

зависимы и могут быть положительными или отрицательными). Тогда выражение коэффициента передачи следящего измерителя примет вид

K1' = K 0.пр.+ ∆ K р K0.пр.

K 0.пр.+ ∆ K с

Здесь K1' - измененное значение коэффициента передачи; K 0.пр. - исходный

коэффициент усиления приемника.

Если разность фазовых сдвигов, вносимых усилителями суммарного и разностного сигналов, составит ∆ψ , то в выражение (2.62) нужно внести дополнительный множитель cos ∆ψ.

Моноимпульсный радиолокатор на базе ФАР

В этом случае в качестве четырехэлементной антенны, необходимой для следящего измерения двух угловых координат цели, используются четыре подрешетки ФАР. Структура приемника почти не отличается от представленной на рис.2.41. После фазовых детекторов устанавливают электронные интеграторы. Вместо механических приводов антенны используют вычислитель фаз для элементов ФАР.

Если цели могут находиться секторе, превышающем сектор сканирования луча ФАР в горизонтальной плоскости, то дополнительно к электронному управлению лучом антенны в РЛС используют механический привод ФАР.

На рис.2.38,б рассматривался принцип измерения одной угловой координаты при последовательном сравнении сигналов, осуществляемом путем коммутации луча антенны в два положения: 1 и 2. Однако на практике чаще приходится измерять две угловые координаты. Для этого нужно коммутировать ДН антенны в четыре положения в плоскости, перпендикулярной РСЛ (эта плоскость называется картинной), или

осуществлять коническое сканирование луча с частотой f ск.

Первый способ удобнее реализовать при использовании ФАР, а второй - при использовании зеркальной механически управляемой антенны. В последнем случае ось вращения луча (ОА на рис.2.42) является равносигнальной линией.

При смещении источника сигнала с РСЛ принимаемый сигнал оказывается амплитудно-модулированным с частотой сканирования, причем глубина модуляции в первом приближении пропорциональна смещению β, а начальная фаза модуляции соответствует направлению смещения Ψ . На рис.2.42 показаны соотношения в картинной плоскости.

Ωск

β2 B

0 β1

Рис.2.42. Иллюстрация конического сканирования в картинной плоскости

Точка О соответствует РСЛ. Точка А1 представляет направление максимума ДН, точка В - направление на цель. Отрезок ОА1 соответствует углу между РСЛ и линией максимума ДН, отрезок 0B - углу между РСЛ и направлением на цель, т.е. текущей ошибке измерения β. Компоненты ошибки β по двум координатным осям равны

β1 = β cosψ ,

β2 = β sinψ .

Временную зависимость амплитуды принимаемого сигнала можно выразить приближенной формулой

U m (t) =U [1+0,55 µ β cos(Ωскt −ψ )].

Здесь U - амплитуда сигнала, когда источник его находится на равносигнальной линии; Ωск = 2π f ск.

Для упрощения этой формулы введем обозначение

µ1 = 0,55 µ .

Кроме того, добавим гармонический множитель. Тогда сигнал будет иметь вид

U с(t) =U m 1+ µ1 β cos(Ωскt − ψ) cos ω0t , (2.63)

где ω0 - несущая частота, рад/с.

		9
На рис.2.43 представлена структурная схема угломера с коническим
сканированием.
Пр.ант Пр.ант.
АРУ	ФД	УПТ
АРУ	Fск
Приемник	Fск
Приемник	ПФ
	ФД	УПТ
Пр.об.
ГОН
Рис. 2.43. Структурная схема РЛС с коническим сканированием.
Пр.ант.- привод антенны; Пр.об. - привод облучателя; ГОН - генератор
опорных напряжений; ФД - фазовый детектор; УПТ - усилитель постоянного тока; ПФ -
полосовой фильтр; АРУ - автоматическая регулировка усиления.

Облучатель зеркальной антенны вращается приводом с угловой скоростью Ωск. С осью этого привода соединен ротор генератора опорных напряжений (ГОН). На выходах двух ортогональных обмоток ГОН формируются опорные напряжения для фазовых детекторов

U cos Ωскt и U sin Ωскt .

Приемник заканчивается амплитудным детектором, на выходе которого образуется напряжение (см. формулу (2.63))

Кпр U m + Кпр U m µ1 β cos(Ωскt − ψ) , (2.64)

где Кпр - коэффициент усиления приемника.

Устройство АРУ с полосой пропускания ∆f АРУ << f ск стабилизирует постоянную составляющую напряжения в формуле (2.64), т.е.

Кпр U m =U0 .

Переменная составляющая в формуле (2.64) фильтруется и поступает на фазовые детекторы (ФД). Фазовый детектор представляет собой каскадное соединение перемножителя и фильтра нижних частот (ФНЧ). Полоса пропускания ФНЧ 2 πΔf << Ωск. Поэтому на выходах ФД имеем

U1 = Кфд.U 0 µ1βcos ψ и U2 = Kфд . U 0 µ1βsin ψ .

U1 и U2 - это выходные напряжения дискриминатора следящего измерителя. Управляющее устройство измерителя состоит из двух УПТ и приводов, поворачивающих антенну в двух ортогональных плоскостях вплоть до того момента, когда рассогласования βcosψ и βsinψ обратятся в нули. При этом направление на цель определяется положением равносигнальной линии (в данном случае - оси антенны).

Угломер с квадрантным сканированием.

При использовании конического сканирования в РЛС с антенной в виде ФАР ДН перемещается дискретно. Если дискрет перемещения антенны выбрать равным 90°, придем к так называемому квадрантному сканированию. При этом ДН периодически устанавливается в 4 положения, по одному положению на каждый квадрант. Этот метод сканирования иллюстрируется на рис.2.44, на котором координатные оси X и Y находятся в картинной плоскости, параллельной плоскости ФАР. Точки 1,2,3,4 представляют собой пересечения картинной плоскости с осью ДН ФАР в последовательные моменты времени.

2 4 x

Рис. 2.44. Иллюстрация метода квадрантного сканирования Метод квадрантного сканирования был кратко описан в монографии [2]

применительно к зеркальной антенне с механически управляемым облучателем, периодически занимающим 4 положения. Известно также о применении этого метода в аэрологических радиолокаторах. В данном разделе рассматривается применение метода квадрантного сканирования к РЛС с ФАР.

Реализовать квадрантное сканирование можно двумя способами. Первый заключается в использовании соответствующей программы изменения фазового распределения в ФАР, обеспечивающей последовательные отклонения ДН вверх - влево - вниз - вправо. Второй способ предусматривает установку на выходах четырех подрешеток ФАР дополнительных управляемых фазовращателей 0 ÷ π/2 с последующими сумматорами. Нами рекомендуется второй путь, преимущества которого выяснятся из последующего изложения.

Структурная схема РЛС с рассматриваемым методом сканирования представлена на рис.2.45.

ФАР					АРУ
				+	АРУ
A B		ФВР-A	ФВР-B	+
A B				+	Прием
C D		ФВР-C	ФВР-D	+	Прием
C D				+
				+
		Вычисли-	АЦП1	ФД1
к ФВР-A		Вычисли-
к ФВР-A		тель фаз	АЦП2	ФД2
B	C		АЦП2	ФД2
B
		К ФВР-D
		К ФВР-D
		ГОН

Рис. 2.48. Блок - схема устройства квадрантного сканирования. ФВР - фазовращатель, АРУ – автоматическая регулировка усиления, Прием – приемник, ФД–фазовый детектор, АЦП – аналого – цифровой преобразователь,

ГОН – генератор опорных напряжений.

Суммарные напряжения на выходах четырех подрешеток А, В, С, D подключаются к фазовращателям с управляемыми фазовыми сдвигами. Фазовые сдвиги в фазовращателях принимают значения 0 или π/2. Управляющие числа поступают из генератора опорных напряжений. Управляющее число нуль устанавливает нулевой фазовый сдвиг, число 1 устанавливает фазовый сдвиг π/2. Если во всех фазовращателях фазовые сдвиги отсутствуют, диаграмма направленности ФАР находится в условно нулевом положении, определяемом фазовым распределением в подрешетках. Это направление совпадает с равносигнальной линией антенны.

Временные диаграммы фазовых сдвигов в фазовращателях представлены на рис.2.46. На первом интервале времени в фазовращателях А и В устанавливаются сдвиги π/2, а в фазовращателях С и D - нулевые сдвиги. При этом ДН антенны смещается вверх. Такое направление смещения объясняется тем, что максимум ДН

находится в положении, в котором пространственные сдвиги фаз (ϕпр ) в подрешетках ФАР С и D равны введенным фазовым сдвигам в элементах А и В.

π/2
π/2	A
0		t


π/2
π/2	B
0	B	t
0		t
π/2	C
π/2
0		t
0		t
π/2	D
π/2
0		t
0		t

Рис.2.46. Временные диаграммы фазовых сдвигов Рассчитаем величину смещения ДН ФАР α с помощью рис.2.47

		Сигнал
LA	A, B
LA	α	α
	C, D

Рис.2.47. К расчету смещения ДН ФАР Пространственный сдвиг фазы в элементах ФАР С и D равен

ϕ = 2λπ ∆ sin α = 2λπ 0,5 LA sin α .

Приравнивая ϕпр = π2 , получим

sin α = 2 λLA ≈ 12θc .

Здесь θс - ширина ДН антенной решетки по суммарному сигналу. Поскольку на практике θс равна немногим долям радиана, величина sin α << 1. При этом sin α ≈ α . В результате имеем

α = 0,5 θс. (2.65)

Если в элементах А и В фазовые сдвиги будут нулевыми, а в эл ементах С и D установлены фазовые сдвиги, равные π/2, очевидно, что ДН ФАР сместится вниз на

α = −0,5 θс. Следовательно, при коммутации фазовых сдвигов на выходах подрешеток А+В и С+D диаграммы направленности ФАР пересекаются на уровне –3дБ относительно максимума.

Заметим, что то же самое имеет место в угломере с коническим сканированием. Из соотношения (2.65) следует, что всегда

α = 0,5 .

θс

Аналогично, если фазовые сдвиги π/2 будут установлены в элементах А и С, а в элементах В и D – сдвиги будут отсутствовать, ДН ФАР сместится влево. И, наконец, если фазовые сдвиги π/2 установить в элементах В и D, а в элементах А и С оставить нулевые фазы, диаграмма направленности ФАР отклонится вправо относительно РСЛ.

Теперь определим зависимость формы огибающей напряжения на входе приемника от знака углового смещения β источника сигнала с равносигнальной линии. Предположим вначале, что β > 0, т.е. источник сигнала смещен вверх с равносигнальной линии. Тогда максимум принятого сигнала будет иметь место при отклонении ДН антенны вверх относительно РСЛ, т.е. при фазовых сдвигах π/2 в элементах А и В. Если максимум ДН отклонить вниз (сдвиги фазы на π/2 в эл ементах С и D), принятый сигнал будет минимальным. Если фазовые сдвиги π/2 установить в элементах А и С или В и D, принятый сигнал будет принимать некоторое среднее значение.

Временная зависимость огибающей принятого сигнала (при β> 0) представлена на рис.2.48, а. Опорные напряжения фазовых детекторов даны на рис.2.48, б и рис.2.48, в.

U(t)

AB AB

AC BD

t a

U оп.1

-1

U оп.2

-1

Рис.2.48. Огибающая сигнала (a) и опорные напряжения (б, в). Сопоставляя названные рисунки, приходим к следующим выводам:

-напряжение на выходе фазового детектора ФД1>0,

-напряжение на выходе фазового детектора ФД2 равно нулю.

Эти результаты соответствуют смещению β>0 (в вертикальной плоскости) и отсутствию смещения источника сигнала относительно РСЛ в горизонтальной плоскости.

При квадрантном сканировании можно избежать потерь в отношении сигнал/шум в канале сопровождения по дальности. Для этого достаточно обнулять все фазовращатели на выходах подрешеток в моменты излучения зондирующего импульса.

Кроме того, поскольку зондирующий сигнал не модулирован с частотой сканирования, потенциальный противник не имеет информации о величине этой частоты и не может сформировать ответную помеху.

В рассмотренном устройстве частоту сканирования можно сделать весьма высокой (до одной четверти частоты следования импульсов). Это позволяет, в соответствии с формулой (2.60), значительно уменьшить погрешность из-за амплитудных флуктуаций сигнала цели.

По аппаратурным затратам метод квадрантного сканирования эквивалентен методу конического сканирования, но выигрывает у последнего в быстродействии. Этот выигрыш связан с тем, что для изменения положения ДН антенны достаточно изменить фазы в четырех однобитных фазовращателях, а не во всех фазовращателях ФАР

Следящий измеритель дальности.

Принцип измерения дальности целей в радиолокаторе с непрерывным излучением приведен в разделе 1.4.6. В данном разделе рассматриваются структура и характеристики цифрового следящего дальномера в импульсном радиолокаторе. Структурная схема дальномера с расщепленным стробом представлена на рис.2.49.

От при –		Временной
емника	АЦП	Временной	x m	Интегратор
емника	АЦП	дискриминатор	x m	Интегратор
		дискриминатор
		Формирование		Управляемая
		стробов		задержка

Рис.2.49. Структурная схема дальномера Каждый импульс отраженного сигнала оцифровывается в АЦП и поступает на

вход временного дискриминатора. Число на выходе дискриминатора пропорционально различию (рассогласованию δt ) временных положений сигнала цели и расщепленного строба. Последний состоит из первого и второго стробов. Число на выходе интегратора

U инт изменяется со скоростью, пропорциональной рассогласованию. В результате, временная задержка стробов (преобразователь на рис.2.49), управляемая значением

U инт , изменяется в нужную сторону. Это приводит к уменьшению рассогласования до нуля при сопровождении неподвижной цели. Число на выходе интегратора пропорционально дальности цели.

Структура дискриминатора дана на рис.2.50, временные диаграммы - на рис.2.51.

1-й строб
	Управляемый	Интегратор 1
	ключ 1	Интегратор 1
Вход	ключ 1		Выход
Вход		+	Выход
		+
	Управляемый	Интегратор 2
	ключ 2	Интегратор 2
	ключ 2
2-й строб

Рис.2.50. Структурная схема временного дискриминатора Дискриминатор состоит из двух нормально запертых ключей, отпираемых

соответственно первым и вторым стробами, двух накопителей и сумматора. По переднему фронту первого строба выходы накопителей обнуляются. Затем в первом накопителе суммируются со знаком минус дискретные выборки сигнала цели в пределах

первого строба. Их сумму обозначим Σ1. С окончанием первого строба первый ключ запирается, а с появлением второго строба открывается второй ключ. При этом во втором накопителе суммируются со знаком плюс выборки сигнала в пределах второго

строба. Их сумму обозначим Σ2. На выходе сумматора к концу второго строба формируется число Σ2 + Σ1, пропорциональное рассогласованию δt .

	б
1	2

Рис.2.51. Временные диаграммы

дискриминатора: а-огибающая сигнала, б – дискретизованная огибающая, в – стробы

В примере на рис.2.51 выходное число дискриминатора Σ2 + Σ1 < 0 . Поэтому число на выходе интегратора уменьшается. Вследствие этого уменьшается задержка

стробов, что приводит к уменьшению рассогласования. В дальнейших периодах следования импульсов рассогласование уменьшается до нуля, если цель неподвижна и отношение сигнал/шум больше единицы.

Если отношение сигнал/шум невелико, может появиться заметная шумовая погрешность σR . При сопровождении движущейся цели могут присутствовать динамические ошибки. При этом часто наибольший вес имеет ошибка, вызванная радиальной скоростью цели. Для уменьшения этой ошибки целесообразно использовать дальномер с астатизмом второго порядка.

Устройства слежения за частотой сигнала цели

Слежение за частотой отраженного сигнала используется для решения двух задач: удержания частоты сигнала в пределах полосы пропускания согласованного

фильтра; измерения доплеровского смещения частоты сигнала (радиальной скорости цели).

Структура аналогового следящего устройства представлена на рис.2.52. Собственно следящая система обведена штриховой рамкой. Вне рамки находятся блоки, используемые в случае необходимости измерения доплеровского смещения частоты.

		Выход
От приемника	СМ	Согласован-	Дискримина -	t	ГУН
f пр+ f д	СМ	ный фильтр	тор	∫0	ГУН
f пр+ f д		ный фильтр	тор	∫0

Частотомер – UF

U fд

Рис. 2.52.Структурная схема следящего измерителя частоты

f пр – промежуточная частота, f д – частота Доплера, ГУН – генератор, управляемый напряжением,

U fд – напряжение, пропорциональное частоте f д ,

UF - напряжение, пропорциональное частоте f пр − f 0 .

Дискриминатор следящей системы включает в себя смеситель, согласованный фильтр и частотный детектор. Аналоговый частотный детектор можно построить на двух расстроенных резонансных контурах. Частотные характеристики контуров приведены на рис.2.53.

	Резонансный	АД
	контур 1
Вход			Выход
		–

Резонансный АД контур 2

f0 f

	б)
	U д
0	f0	f
		f

	в)

Рис.2.53. Аналоговый частотный дискриминатор

a– структурная схема, б – частотные характеристики резонансных контуров,

в– характеристика частотного дискриминатора; АД - амплитудный детектор.

Если частота генератора, управляемого напряжением (ГУН),

f ГУН = f инт − f 0 + f д,
частота сигнала после смесителя равна ƒ0,	и напряжение на выходе

дискриминатора отсутствует. При этом выходное напряжение интегратора остается неизменным.

Если доплеровская частота возрастет на δf

δf . Напряжение на выходе интегратора будет возрастать до тех пор, пока частота управляемого

генератора f ГУН не повысится на		δf . В результате частота напряжения на входе
согласованного фильтра вернется		к значению f 0,		а выходное напряжение
дискриминатора обратится в нуль.
Цифровой вариант дискриминатора в устройстве слежения за частотой
представлен на рис.2.54.
					Выход
вход	Цифровой частотный		–		Выход
вход	Цифровой частотный		–
		детектор
		детектор

Рис. 2.54. Цифровой частотный дискриминатор; N – число, пропорциональное частоте f0 .

В дискриминаторе используются счетчик числа периодов колебания на выходе согласованного фильтра в течение интервала времени Tcr и узел вычитания. Число на выходе счетчика равно f1 Tcr , где f1 - это частота сигнала на входе дискриминатора. Это число поступает на первый вход вычитатется. На второй вход этого узла подается постоянное число, равное f0 Tcr , где f0 - частота настройки согласованного фильтра. Число на выходе вычитателя равно

(f 0 − f 1)Tcr .

Если f 1 ≠ f 0 , то напряжение на входе интегратора не равно нулю. Изменяющееся напряжение на выходе интегратора подстраивает частоту управляемого генератора так, что

f 1 → f 0 .

Задание на самостоятельную проработку

Описание активных и интерактивных методов обучения.

Литература

1.Незлин Д.В. Радиотехнические системы: Уч. пособие. - М.:МИЭТ, 2007. - 250 с.:

ил. – С.78-85

3.“Известия высших учебных заведений. Электроника”

http://www.mocnit.miee.ru/redaction/. 4. http://ru.wikipedia.org/

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в папке Литература

#
10.09.20231.49 Mб56Nezlin.pdf
#
10.09.2023873.23 Кб18Razreshenie_2021_stud.pdf
#
10.09.202315.09 Mб30бакулев радиолокация распозн.pdf
#
10.09.202324.06 Mб37бакулев радиолокация.pdf
#
10.09.202316.52 Mб461Гришин Ю.П., Ипатов В.П., Казаринов Ю.М. Радиотехнические системы (1990).pdf
#
10.09.20233.04 Mб65Лекции РТС старые.pdf
#
10.09.202324.8 Mб205М.И.Финкельштейн Основы радиолокации.pdf