Практическое занятие №2
Цифровое устройство формирования и обработки фазоманипулированных сигналов
Цель работы: изучить принципы построения, структуру и основные характеристики цифровых устройств генерирования и оптимальной обработки фазоманипулированных сигналов (ФМС); определить основные характеристики сигналов и устройств.
Продолжительность работы - 4 ч.
Обеспечение занятия: Matlab, программное обеспечение лабораторной работы.
Теоретические сведения
Формирование фазоманипулированных сигналов
Фазоманипулированные сигналы получают
путем коммутации фазы синусоидального
напряжения в определенные моменты
времени на некоторую величину
.
Временная зависимость ФМС выражается
формулой
,
(1)
где
– закон фазовой манипуляции;
– несущая частота сигнала.
В данной работе рассматриваются бинарные
ФМС, начальная фаза которых может
принимать 2 значения: 0 и
.
Структура подобного сигнала иллюстрируется
на рис.1,а.
ФМС содержит определенное число
интервалов с постоянной начальной
фазой. В примере на рис.1 видны четыре
таких интервала:
.
Самые короткие интервалы длительностью
(в данном случае
и
)
называются элементами или дискретами
ФМС. Длительности остальных интервалов
кратны
.
Длительность всего сигнала обозначим
.
Длиной ФМС
называется число дискретов, укладывающихся
на длительности сигнала:
.
Длина ФМС на рис.1 равна семи. Такой сигнал часто называют семиэлементным.
Показано (см., например, [1]), что ширина спектра ФМС примерно равна
. (2)
Следовательно, база сигнала
.
Поскольку обычно
,
ФМС относится к классу сложных сигналов.
Известно также (см., например, [2]), что
разрешающая способность сигнала по
времени
обратна пропорциональна ширине его
спектра:
.
Для ФМС с учетом формулы (2) это означает,
что
.
Различают непрерывные и импульсные
ФМС. Непрерывные ФМС являются
периодическими с периодом
.
База непрерывного сигнала по-прежнему
определяется как
.
Импульсный ФМС состоит из отрезков
длительностью
,
повторяющихся с периодом
.
Комплексная огибающая (комплексная
амплитуда) сигнала
определяется формулой
.
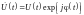Для бинарных ФМС
(рис.1,б). Поэтому
.
Нормированная комплексная огибающая (рис.1,в) равна
.
Если в выражении
минус единицу заменить нулем, получим
кодовую последовательность (сокращенно
– код) ФМС (рис.1,г). Назовем еще одну
характеристику бинарного ФМС - решетчатую
функцию РФ(t), показанную
на рис.1,д. РФ(t) представляет
собой последовательность
-функций
(или единичных импульсов), располагающихся
в началах дискретов. Полярность РФ(t)
совпадает с полярностью комплексной
огибающей соответствующего дискрета
ФМС. Каждая из перечисленных функций:
,
,
код и РФ(t) полностью
определяет структуру ФМС.
Сравнивая рис.1,в и 1,д, видим, что решетчатая функция ФМС представляет собой результат временной дискретизации нормированной комплексной огибающей сигнала с дискретом . Комплексная амплитуда, в свою очередь, является огибающей решетчатой функции.
Распространенными кодовыми
последовательностями ФМС являются
М-последовательности. Текущее значение
М-последовательности (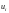
=
0; 1) определяется с помощью рекуррентной
формулы по
предшествующим величинам:
. (3)
Суммирование в формуле (3) выполняется
по модулю 2, коэффициенты
,
,
…,
принимают значения «0» или «1». Число
слагаемых
в правой части выражения (3) называется
памятью последовательности.
Рекуррентная формула (3) просто реализуется
с помощью сдвигового регистра с
сумматором по модулю 2 в цепи обратной
связи (рис.2). Число ячеек в регистре
равно
,
а обратные связи на входы сумматора
берутся с ячеек, номера которых равны
номерам ненулевых коэффициентов
в формуле (3). Схема на рис.2 соответствует
= 3,
=
= 1,
= 0.
На все ячейки регистра подаются тактовые импульсы, осуществляющие сдвиг находящихся в них чисел вправо на 1 разряд. При этом в первую ячейку записывается число с выхода сумматора по модулю 2. О назначении дешифратора нуля будет сказано позднее.
В таблице поясняется процесс формирования М-последовательности устройством, изображенным на рис.2, при начальных значениях элементов , равных единице. Числа в первом столбце таблицы – это номера тактовых интервалов. Следующие три столбца содержат числа в 1-й, 2-й и 3-й ячейках регистра. Последний столбец – числа на выходе сумматора по модулю 2.