25. Охарактеризуйте временные диаграммы переходных процессов логических элементов.

Эффективным средством анализа переходных процессов в схемах являются временные диаграммы. При их построении состояние неопределенности изобра­жают одним из двух способов, которые показаны для элемента И (рис. 2а). Изо­бражение на рис. 2б строже, но менее наглядно; изображение на рис. 2в нагляд­нее, но может быть спутано с состоянием высокого импеданса элемента, имеюще­го три состояния выхода.

Рисунок 2.- Способы изображения состояния неопределенности логического элемента

Линии со стрелками обозначают причинно-следственные отношения в це­почке переключений. Линия начинается на фронте, который непосредственно вы­зывает переключение рассматриваемого элемента и оканчивается стрелкой на фронте выходного сигнала этого элемента. Наличие таких указателей заметно об­легчает понимание работы сложных схем.

На рис. 3а показан фрагмент схемы и варианты начертания временных диа­грамм переходных процессов. Здесь и в дальнейшем для обозначения выходного сигнала элемента используется номер самого элемента. Диаграмма на рис.3б иг­норирует переходные процессы в элементах и схеме. Такие диаграммы применя­ют, когда основной целью является иллюстрация логических и причинно-следственных отношений, а длительностью переходных процессов по сравнению с интервалами между поступлением сигналов можно пренебречь.

Диаграмма на рис. 3а построена в предположении, что все элементы имеют максимально возможные значения задержки. Эта диаграмма наглядна, поэтому удобна для первого знакомства с поведением сложной схемы. Но она годится лишь для оценки максимальной длительности переходного процесса. Делать по такой диаграмме выводы о состояниях элементов во время переходного процесса нельзя: это лишь один частный случай из множества возможных процессов.

Рисунок 3. - Временные диаграммы переходных процес­сов:

а - фрагмент схемы; б, в, г - изображение переходных процес­сов; б - без учета задержек элементов, в - в предположении, что за­держки максимальны; г - с использованием состояния неопределен­ности

Диаграмма рис. 3г учитывает состояния неопределенности элементов в со­ответствии с (1). Она достаточно строго моделирует поведение схемы при любых комбинациях задержек, допускаемых паспортами элементов. Полезно сравнить диаграммы на рис. 3 в и г, обращая внимание на их расхождения, причиной кото­рых является общность диаграммы г и частность диаграммы в.

Быстрое чтение и особенно построение временных диаграмм требуют неко­торой тренировки. Полезно самостоятельно построить несколько вариантов диа­грамм, изменяя моменты поступления входных сигналов и соотношения задержек элементов схемы на рис. 3а. Построение диаграммы нужно начинать с тех эле­ментов, для которых известны все входные сигналы, в данном примере - с эле­мента 1. После определения выхода элемента 1 известными становятся все входы элемента 2 и т. д. Если построение диаграммы с учетом состояния неопределенности вызывает затруднение, можно рекомендовать сначала построить диаграмму с нулевыми задержками, показанной на рис. 3б, затем на том же чертеже нало­жить на нее диаграмму с максимальными задержками, после чего интервалы со­стояний неопределенности выделяются намного легче.

26. Раскройте понятие гонок в логических схемах.

В логических схемах встречаются участки, где сигнал разветвляется, получившиеся два сигнала распространяются по двум независимым цепочкам элементов, а затем оба сигнала снова встречаются на входах одного элемента.

Пусть в тракте чет четное число инверторов, а в тракте нечет - нечетное. Анализ подобной схемы методами алгебры Буля без учета задержек даст на ее выходе 0 при любом значении входного сигнала. Но реальные элементы имеют конечную задержку срабатывания. Обозначим задержки в трактах чет и нечет через Тчет и Тнечет. В зависимости от соотношения этих величин получится один из процессов, изображенных на рисунке 1 в и г. В обоих случаях в выходном сигнале появится помеха, не предусмотренная булевыми выражениями.

При достаточно большой разности Тчет и Тнечет помеха будет иметь длительность, во много раз превышающую время переключения элемента, и амплитуду, равную номинальному сигналу. Это уже полноценный логический сигнал, на который могут реагировать последующие элементы. Если выход схемы подключен к запоминающему элементу (триггеру), то помеха может запомниться, и будет влиять на последующие процессы в устройстве. Если выход схемы подан в качестве обратной связи на вход, там появится непредвиденный сигнал, который может вызвать непредвиденное повторное срабатывание этой же схемы.

Описанное явление называют гонками или состязаниями (races). Два сигнала идут разными путями, и схема может реагировать на них по-разному (верно или неверно) в зависимости от того, какой сигнал выиграет гонку.

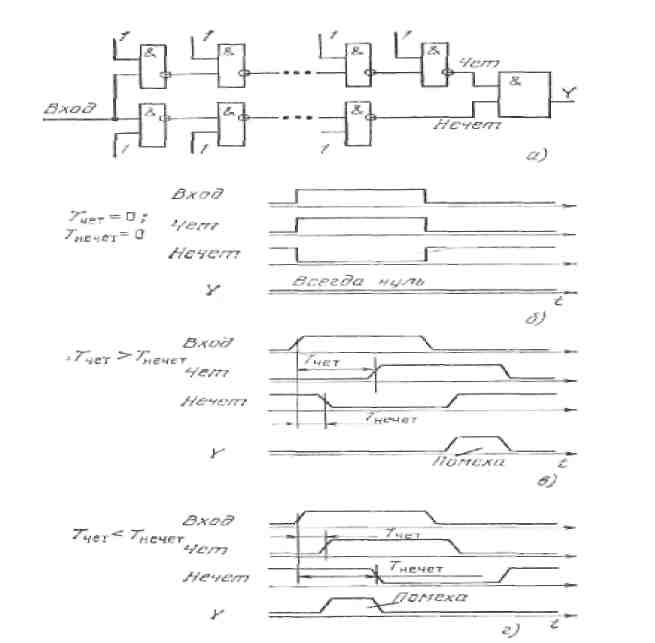
Рисунок 1 – Варианты временных диаграмм (б, в, г), иллюстрирующие гон­ки в логической схеме (а)

Распространены три метода борьбы с гонками: введение тактирования, построение противогоночных схем и учет минимального времени задержки.

1. Наиболее универсальным, эффективным и поэтому широко используемым методом борьбы с гонками является тактирование. Основная суть его заключается в следующем. По всему цифровому устройству разводится единая система тактирующих (синхронизирующих) сигналов. В широко распространенной двухтактной или двухфазной системе синхронизации используются две периодические последовательности синхросигналов - синхросигнал С1 и синхросигнал С2.

2. Противогоночные схемы - это схемы, построенные так, что в них если и возникают, то только неопасные гонки, то есть такие, при которых отсутствует риск появления на выходе сигналов, не предусмотренных логическим выражением. Примером неопасной гонки может служить гонка фронта по двум трактам, в каждом из которых содержится четное (или в каждом нечетное) число инверторов и которые объединяются на выходах элементом ИЛИ: кто бы ни выиграл гонку, результат все равно будет верный, изменится лишь задержка его получения. Для исключения опасных гонок можно вводить в схему дополнительные связи и элементы так, чтобы нежелательные параллельные пути запирались самим входным сигналом еще до достижения им опасной развилки тракта.

3. Учет минимального времени задержки. Если известно минимально возможное время задержки элемента, то во многих практически важных случаях можно постулировать отсутствие гонок. Пусть в схеме на рис. 1а глубина цепочки Чет настолько больше глубины цепочки Нечет, что задержка в длинной цепочке, даже если последняя состоит только из самых быстрых элементов, будет все равно больше задержки сигнала в короткой цепочке, даже если в нее попадут только самые медленные элементы. Схема со столь большой разницей в длине путей всегда будет вести себя так, как показано на рис. 1в. То есть, пока входной сигнал равен единице, помеха на выходе не появится.

Гонки по входу. Гонки по входу возникают, когда ветвящийся сигнал поступает на элементы, имеющие разброс по уровню срабатывания (рис. 2а), а фронт этого сигнала излишне пологий (рис. 2б). Если длительность фронта входного сигнала заметно больше времени срабатывания элементов, то где-то в середине фронта будет существовать отрезок времени, когда с точки зрения одного элемента входной сигнал уже равен 1, а с точки зрения другого - еще равен 0. Элементы будут реагировать на один и тот же сигнал как на два различных, а такая ситуация при проектировании схемы ее алгоритмом не предусматривается. В результате схема в течение этого времени может выработать ложные сигналы. Это явление и называют «гонки по входу».

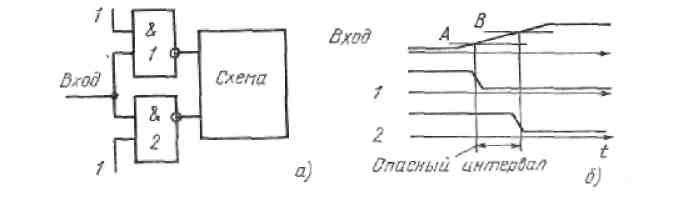
Рисунок 2 – Гонки по входу: иллюстрация условий их возникновения