
- •ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
- •Введение
- •3.1.Приведение сходящейся системы сил к центру
- •5.5.Уравнения равновесия плоской произвольной системы сил
- •Введение
- •Круг проблем, рассматриваемых в механике, очень велик и с развитием этой науки в
- •При изучении какого-либо явления необходимо выделять в нём наиболее существенное, главное, абстрагируясь от
- •Таковыми и являются законы, теоремы и принципы теоретической механики, которые установлены в результате
- •Статика твёрдого тела
- •Задачи статики
- •1. Основные понятия статики
- •1.2. Свободное (несвободное) твёрдое тело
- •Тело, перемещениям которого в пространстве препятствуют другие тела, называется несвободным, рис. 2.
- •1.3. Сила. Система сил
- •Совокупность нескольких сил, действующих на тело называется системой сил.
- •Сила, эквивалентная по своему действию на данное тело данной системе сил называется её
- •1.4. Проекция силы на ось
- •Пример 1
- •Задание 1
- •1.5. Определение модуля силы
- •Пример 2
- •Направляющие косинусы:
- •Задание 3
- •1.6. Главный вектор системы сил
- •Направление главного вектора определяется направ- ляющими косинусами
- •Задание 4
- •Решение
- •1.7. Момент силы относительно точки
- •Вектор момента приложен в точке О и направлен перпендикулярно плоскости, прохо-дящей через центр
- •Рис. 5 Модуль вектора момента равен
- •Геометрически модуль момента силы относительно точки может быть представлен как удвоенная площадь треугольника,
- •Для сил, расположенных в одной плоскости применяется алгебраический момент.
- •Момент считается положительным, когда сила стремится повернуть тело вокруг центра О против хода
- •2) момент силы относительно точки равен нулю, когда линия действия силы проходит через
- •Пример 3
- •Находим моменты этих сил относительно точки А.
- •1.8. Момент силы относительно оси
- •1)строим плоскость, перпендикулярную оси;
- •2) проецируем силу на эту плоскость;
- •3) находим плечо проекции силы относительно точки пересечения оси с плоскостью;
- •4) вычисляем произведение проекции силы на плечо;
- •Момент силы относительно оси равен нулю, если: 1)сила параллельна оси; 2)линия действия силы
- •Момент силы относительно точки связан с моментом силы относительно оси, проходящей через эту
- •где , , – углы между направлением векторного момента силы и положительными направлениями
- •1.9. Главный момент системы сил
- •Направление главного момента определяется направ- ляющими косинусами
- •2. Аксиомы статики
- •Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если
- •Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, прило-
- •На первом рисунке равнодействующая двух сил приложена в точке А. На втором рисунке
- •Аксиома 4. Силы, взаимодействия двух тел равны по величине противоположны по направлению и
- •3. Сходящаяся система сил
- •Приведём эту систему сил к центру С. Для этого применим следствие из второй
- •Сложим эти силы по правилу треугольника, рис. 17.
- •3. 2. Условия равновесия сходящейся системы сил
- •Следовательно, будет равен нулю и главный вектор этой системы сил.
- •Так как главный вектор равен геометрической сумме сил, то эта сумма также будет
- •Введём координатные оси Оxyz и спроецируем векторную сумму сил
- •Если тело находится в равновесии под действием плоской сходящейся системы сил, рис. 18
- •3.3. Теорема о трёх силах
- •4. Теория пар сил
- •Пары, расположенные в одной плоскости образуют плоскую систему пар, рис. 22. Пары, расположенные
- •4.2. Момент пары сил
- •Таким образом момент пары сил равен главному моменту сил пары относительно любого центра.
- •Если рассматриваются пары сил, лежащие в одной плоскости, то эту плоскость совмещают с
- •Момент каждой пары равен произведению силы пары на плечо взятому со своим знаком.
- •Из доказанного следует, что момент пары сил не изменяется, в следующих случаях:
- •2) при повороте пары сил в плоскости её действия;
- •3) при переносе пары сил из плоскости её действия в параллельную плоскость.
- •4.3. Сложение моментов пар сил
- •Векторы моментов пар – свободные векторы. Поэтому выберем произвольную точку С и перенесём
- •Складывая векторы моментов пар, получим многоугольник, замыкающей стороной которого будет момент пары, эквивалентной
- •При сложении пар сил, расположенных в плоскости, моменты пар складываются алгебраически. Результи- рующая
- •4.4. Условия равновесия пар сил
- •Если тело находится в равновесии, под действием системы пар, расположенных в одной плоскости,
- •5. Приведение сил к центру
- •Приложим в точке O две уравновешенные силы F 'и F '' , параллельные
- •5.2. Теорема о приведении системы силы к центру
- •Выберем произвольную точку тела О и перенесём в неё все силы, применяя теорему
- •В результате в точке О будут приложены две группы векторов:
- •Сложим пары силы M1, M2 ,..., Mn.В результате полу- чим пару сил, момент
- •5.3. Условия равновесия произвольной системы сил
- •5.4. Уравнения равновесия произвольной системы сил
- •Таким образом, если тело под действием приложенной к нему системы сил находится в
- •Построим декартова координатные оси с началом в центре приведения сил.
- •В результате получим:
- •Используя связь между моментом силы относительно точки и моментом силы относительно оси, проходящей
- •Таким образом, если твёрдое тело находится в равновесии под действием произвольной системы сил,
- •5.5. Уравнения равновесия плоской произвольной системы сил
- •Плоская произвольная система сил является частным случаем пространственной произвольной системы сил.
- •Таким образом, если твёрдое тело находится в равновесии под действием плоской произвольной системы
- •Из представленных уравнений три уравнения для плоской произвольной системы сил являются
- •6. Связи и силы реакций связей
- •Сила реакции связи – сила, с которой связь дей- ствует на рассматриваемое тело.
- •При действии тела ребром на гладкую поверхность сила реакции направлена по нормали к
- •Сферический шарнир - устройство, обеспечиваю- щее движение тела вокруг одной его неподвижной точки.
- •Невесомый стержень – это стержень, весом которого по сравнению с воспринимаемой им нагрузкой
- •Шероховатая поверхность - поверхность, трение которой учитывают при решении задач.
- •В расчетах сила реакции шероховатой поверхности представляется в виде двух составляющих: силы, перпендикулярной
- •Жесткая заделка («заделка») - связь, обеспечива- ющая неподвижное закрепление оконечности бруса.
- •Если брус находится под действием сил, расположенных произвольно в пространстве, то силы реакции
- •7. Решение задач статики
- •2. Составить расчётную схему задачи в следующей последовательности:
- •г) выбрать оси координат, если планируется анали- тическое решение задачи.
- •8. Центр тяжести
- •Равнодействующая двух параллельных сил, направ- ленных в одну сторону, равна сумме этих сил:
- •Чтобы найти положение точки приложения равно- действующей двух параллельных сил, воспользуемся теоремой Вариньона.
- •получим:
- •8.2. Центр системы параллельных сил
- •Так как положение точки С от направления параллельных сил не зависит, то повернём
- •модуль которой равен
- •Применяем теорему Вариньона относительно оси x.
- •Повернём силы параллельно оси y и применим
- •8.3. Центр тяжести твёрдого тела
- •Силы тяжести, действующие на каждую частицу твёрдого тела образуют систему сил, параллельных вертикальной
- •Если тело является однородным, то вес pk любой его частицы пропорционален объёму vk
- •Если твёрдое тело выполнено в форме пластины, то координаты его цента тяжести определяются
- •Координаты центра тяжести линии определяются по следующим формулам:
- •8.4. Способы определения координат
- •2. Разбиение. Если тело можно разбить на конечное
- •3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам,
- •4. Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести
- •5. Экспериментальные способы. Центры тяжести неоднородных тел сложной конфигурации можно определить экспериментально. Один
- •СПАСИБО ЗА ВНИМАНИЕ
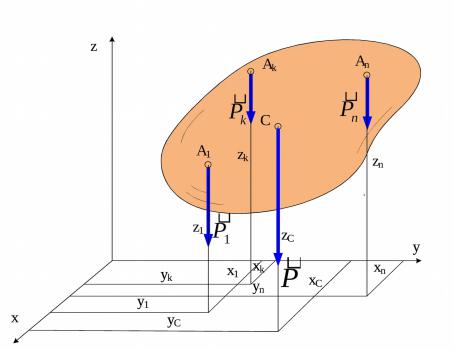
8.3. Центр тяжести твёрдого тела
Центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любом поло- жении тела в пространстве.
147
Силы тяжести, действующие на каждую частицу твёрдого тела образуют систему сил, параллельных вертикальной оси z. Поэтому координаты центра тяжести твёрдого тела определяются по формулам, по которым определяется центр параллельных сил.
|
n |
|
n |
|
n |
|
x |
pk xk |
; y |
pk yk |
; z |
pk zk |
. |
k 1 |
k 1 |
k 1 |
||||
|
|
|
||||
C |
P |
C |
P |
C |
P |
|
|
|
|
|
148
Если тело является однородным, то вес pk любой его частицы пропорционален объёму vk этой части тела:
pk vk , где – удельный вес тела.
Подставляя pk в формулы координат центра тяжести тела, получим координаты центра тяжести объёма.
|
n |
|
n |
|
|
|
n |
|
x |
vk xk |
; y |
vk yk |
; z |
|
|
vk zk |
. |
k 1 |
k 1 |
C |
k 1 |
|||||
|
|
|
||||||
C |
V |
C |
V |
|
|
V |
|
|
|
|
|
|
|
|
149
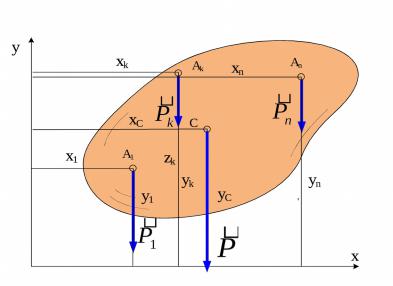
Если твёрдое тело выполнено в форме пластины, то координаты его цента тяжести определяются по
формулам: |
n |
|
n |
|
|
|
|
||
x |
sk xk |
; y |
sk yk |
, |
k 1 |
k 1 |
|||
|
|
|||
C |
S |
C |
S |
|
|
|
|
где S – площадь пластины; sk – площади частей, из
которых состоит пластина. |
150 |
Координаты центра тяжести линии определяются по следующим формулам:
|
n |
|
n |
|
n |
|
x |
lk xk |
; y |
lk yk |
; z |
lk zk |
, |
k 1 |
k 1 |
k 1 |
||||
|
|
|
||||
C |
L |
C |
L |
C |
L |
|
|
|
|
|
где L – длина всей линии; lk –длина её частей.
151
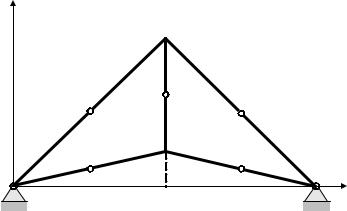
8.4. Способы определения координат |
|
|||||||
|
центров тяжести тел |
|
||||||
1. Симметрия. Если однородное тело имеет |
||||||||
плоскость, ось или центр симметрии, то его центр |
||||||||
тяжести лежит соответственно или в плоскости |
||||||||
симметрии, |
или на оси |
|
симметрии, или в |
центре |
||||
симметрии. |
y |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|||
|
C5 |
C4 |
|
|
|
C3 |
|
|
|
|
|
5 |
|
|
|
||
|
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
E |
|
|
|
|
3 |
|
|
|
1 |
|
|
2 |
C2 |
|
||
|
|
|
|
|
|
|||
|
C1 |
|
|
|
|
B |
|
|
|
A |
|
|
|
|
|
|
|
|
F |
|
|
|
x |
|
||
|
|
|
|
|
|
|||
n
lk yk
y |
k 1 |
|
|
|
|
|
|
C |
l |
|
|
|
|
152 |
|
|
|
|
|
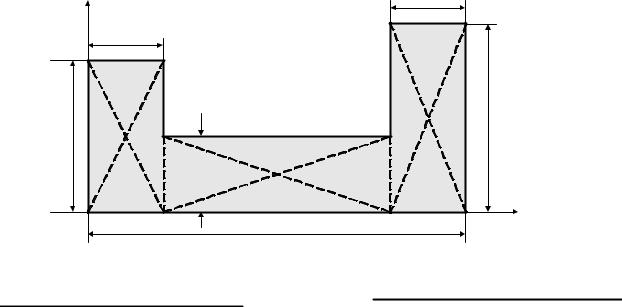
2. Разбиение. Если тело можно разбить на конечное |
||||||
число таких частей, для каждой из которых положение |
||||||
центра тяжести известно, то координаты центра |
||||||
тяжести всего тела можно вычислить по формулам, |
||||||
приведенным выше. При этом число слагаемых в |
||||||
каждом из числителей будет равно числу частей, на |
||||||
которые разбитоy |
тело. |
|
20 |
|
||
|
20 |
|
|
|
|
|
40 |
|
|
20 |
|
50 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
||
|
|
|
100 |
|
x |
|
x s x s |
|
x s |
yc |
y1s1 y2s2 y3s3 |
|
|
x 1 1 |
2 |
2 |
3 3 |
S |
|
|
c |
S |
|
|
|
153 |
|
|
|
|
|
|||
3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
A
|
E |
C |
O |
|
x |
|
xc |
|
|
|
B
x Fk xk F1x1 F2 x2 |
||
c |
F |
F1 F2 |
|
||
154
4. Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объемы vk , для которых формулы из для определения центра тяжести тела принимают вид:
|
n |
|
n |
|
|
|
n |
|
x |
xk vk |
; y |
yk vk |
; z |
|
|
zk vk |
. |
k 1 |
k 1 |
C |
k 1 |
|||||
|
|
|
||||||
C |
V |
C |
V |
|
|
V |
|
|
|
|
|
|
|
|
Затем переходят к пределу, устремляя к нулю. Тогда стоящие в числителях суммы обращаются в интегралы, распространенные на весь объем тела:
155
x |
1 |
|
x dV ; y |
1 |
|
y dV ; z |
|
|
1 |
|
z dV. |
|
|
C |
|
||||||||
C |
V (V ) |
C |
V (V ) |
|
V (V ) |
|
|||||
|
|
|
|
|
|||||||
Аналогично для координат центров тяжести плоского тела и весомой линии получим:
|
|
x |
1 |
|
x dS; y |
1 |
|
y dS. |
|
|||||||||
|
|
S (S ) |
S (S ) |
|
||||||||||||||
|
|
C |
|
|
|
C |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
1 |
|
x dL; |
y |
1 |
|
y dL; z |
|
|
1 |
|
z dL. |
||||||
L (L) |
L (L) |
C |
L (L) |
|||||||||||||||
C |
|
|
|
C |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
156
