
- •ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
- •Введение
- •3.1.Приведение сходящейся системы сил к центру
- •5.5.Уравнения равновесия плоской произвольной системы сил
- •Введение
- •Круг проблем, рассматриваемых в механике, очень велик и с развитием этой науки в
- •При изучении какого-либо явления необходимо выделять в нём наиболее существенное, главное, абстрагируясь от
- •Таковыми и являются законы, теоремы и принципы теоретической механики, которые установлены в результате
- •Статика твёрдого тела
- •Задачи статики
- •1. Основные понятия статики
- •1.2. Свободное (несвободное) твёрдое тело
- •Тело, перемещениям которого в пространстве препятствуют другие тела, называется несвободным, рис. 2.
- •1.3. Сила. Система сил
- •Совокупность нескольких сил, действующих на тело называется системой сил.
- •Сила, эквивалентная по своему действию на данное тело данной системе сил называется её
- •1.4. Проекция силы на ось
- •Пример 1
- •Задание 1
- •1.5. Определение модуля силы
- •Пример 2
- •Направляющие косинусы:
- •Задание 3
- •1.6. Главный вектор системы сил
- •Направление главного вектора определяется направ- ляющими косинусами
- •Задание 4
- •Решение
- •1.7. Момент силы относительно точки
- •Вектор момента приложен в точке О и направлен перпендикулярно плоскости, прохо-дящей через центр
- •Рис. 5 Модуль вектора момента равен
- •Геометрически модуль момента силы относительно точки может быть представлен как удвоенная площадь треугольника,
- •Для сил, расположенных в одной плоскости применяется алгебраический момент.
- •Момент считается положительным, когда сила стремится повернуть тело вокруг центра О против хода
- •2) момент силы относительно точки равен нулю, когда линия действия силы проходит через
- •Пример 3
- •Находим моменты этих сил относительно точки А.
- •1.8. Момент силы относительно оси
- •1)строим плоскость, перпендикулярную оси;
- •2) проецируем силу на эту плоскость;
- •3) находим плечо проекции силы относительно точки пересечения оси с плоскостью;
- •4) вычисляем произведение проекции силы на плечо;
- •Момент силы относительно оси равен нулю, если: 1)сила параллельна оси; 2)линия действия силы
- •Момент силы относительно точки связан с моментом силы относительно оси, проходящей через эту
- •где , , – углы между направлением векторного момента силы и положительными направлениями
- •1.9. Главный момент системы сил
- •Направление главного момента определяется направ- ляющими косинусами
- •2. Аксиомы статики
- •Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если
- •Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, прило-
- •На первом рисунке равнодействующая двух сил приложена в точке А. На втором рисунке
- •Аксиома 4. Силы, взаимодействия двух тел равны по величине противоположны по направлению и
- •3. Сходящаяся система сил
- •Приведём эту систему сил к центру С. Для этого применим следствие из второй
- •Сложим эти силы по правилу треугольника, рис. 17.
- •3. 2. Условия равновесия сходящейся системы сил
- •Следовательно, будет равен нулю и главный вектор этой системы сил.
- •Так как главный вектор равен геометрической сумме сил, то эта сумма также будет
- •Введём координатные оси Оxyz и спроецируем векторную сумму сил
- •Если тело находится в равновесии под действием плоской сходящейся системы сил, рис. 18
- •3.3. Теорема о трёх силах
- •4. Теория пар сил
- •Пары, расположенные в одной плоскости образуют плоскую систему пар, рис. 22. Пары, расположенные
- •4.2. Момент пары сил
- •Таким образом момент пары сил равен главному моменту сил пары относительно любого центра.
- •Если рассматриваются пары сил, лежащие в одной плоскости, то эту плоскость совмещают с
- •Момент каждой пары равен произведению силы пары на плечо взятому со своим знаком.
- •Из доказанного следует, что момент пары сил не изменяется, в следующих случаях:
- •2) при повороте пары сил в плоскости её действия;
- •3) при переносе пары сил из плоскости её действия в параллельную плоскость.
- •4.3. Сложение моментов пар сил
- •Векторы моментов пар – свободные векторы. Поэтому выберем произвольную точку С и перенесём
- •Складывая векторы моментов пар, получим многоугольник, замыкающей стороной которого будет момент пары, эквивалентной
- •При сложении пар сил, расположенных в плоскости, моменты пар складываются алгебраически. Результи- рующая
- •4.4. Условия равновесия пар сил
- •Если тело находится в равновесии, под действием системы пар, расположенных в одной плоскости,
- •5. Приведение сил к центру
- •Приложим в точке O две уравновешенные силы F 'и F '' , параллельные
- •5.2. Теорема о приведении системы силы к центру
- •Выберем произвольную точку тела О и перенесём в неё все силы, применяя теорему
- •В результате в точке О будут приложены две группы векторов:
- •Сложим пары силы M1, M2 ,..., Mn.В результате полу- чим пару сил, момент
- •5.3. Условия равновесия произвольной системы сил
- •5.4. Уравнения равновесия произвольной системы сил
- •Таким образом, если тело под действием приложенной к нему системы сил находится в
- •Построим декартова координатные оси с началом в центре приведения сил.
- •В результате получим:
- •Используя связь между моментом силы относительно точки и моментом силы относительно оси, проходящей
- •Таким образом, если твёрдое тело находится в равновесии под действием произвольной системы сил,
- •5.5. Уравнения равновесия плоской произвольной системы сил
- •Плоская произвольная система сил является частным случаем пространственной произвольной системы сил.
- •Таким образом, если твёрдое тело находится в равновесии под действием плоской произвольной системы
- •Из представленных уравнений три уравнения для плоской произвольной системы сил являются
- •6. Связи и силы реакций связей
- •Сила реакции связи – сила, с которой связь дей- ствует на рассматриваемое тело.
- •При действии тела ребром на гладкую поверхность сила реакции направлена по нормали к
- •Сферический шарнир - устройство, обеспечиваю- щее движение тела вокруг одной его неподвижной точки.
- •Невесомый стержень – это стержень, весом которого по сравнению с воспринимаемой им нагрузкой
- •Шероховатая поверхность - поверхность, трение которой учитывают при решении задач.
- •В расчетах сила реакции шероховатой поверхности представляется в виде двух составляющих: силы, перпендикулярной
- •Жесткая заделка («заделка») - связь, обеспечива- ющая неподвижное закрепление оконечности бруса.
- •Если брус находится под действием сил, расположенных произвольно в пространстве, то силы реакции
- •7. Решение задач статики
- •2. Составить расчётную схему задачи в следующей последовательности:
- •г) выбрать оси координат, если планируется анали- тическое решение задачи.
- •8. Центр тяжести
- •Равнодействующая двух параллельных сил, направ- ленных в одну сторону, равна сумме этих сил:
- •Чтобы найти положение точки приложения равно- действующей двух параллельных сил, воспользуемся теоремой Вариньона.
- •получим:
- •8.2. Центр системы параллельных сил
- •Так как положение точки С от направления параллельных сил не зависит, то повернём
- •модуль которой равен
- •Применяем теорему Вариньона относительно оси x.
- •Повернём силы параллельно оси y и применим
- •8.3. Центр тяжести твёрдого тела
- •Силы тяжести, действующие на каждую частицу твёрдого тела образуют систему сил, параллельных вертикальной
- •Если тело является однородным, то вес pk любой его частицы пропорционален объёму vk
- •Если твёрдое тело выполнено в форме пластины, то координаты его цента тяжести определяются
- •Координаты центра тяжести линии определяются по следующим формулам:
- •8.4. Способы определения координат
- •2. Разбиение. Если тело можно разбить на конечное
- •3. Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам,
- •4. Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести
- •5. Экспериментальные способы. Центры тяжести неоднородных тел сложной конфигурации можно определить экспериментально. Один
- •СПАСИБО ЗА ВНИМАНИЕ
В результате получим:
ån Fkx =0;Прån
k=1 |
k=1 |
ån Fky =0;Прån
k=1 |
k=1 |
ån Fkz =0;Прån
k=1 |
k=1 |
ér |
r |
ù |
m |
F0; |
= |
x ê O ( |
k )ú |
|
ë |
r |
û |
ér |
ù |
|
m |
F0; |
= |
y ê O ( |
k )ú |
|
ë |
r |
û |
ér |
ù |
|
m |
F0. |
= |
z ê O ( |
k )ú |
|
ë |
|
û |
104
Используя связь между моментом силы относительно точки и моментом силы относительно оси, проходящей через эту точку, получим
ån
k=1
ån
k=1
ån
k=1
Прx
Прy
Прz
ér ( êm ë O
ér ( êm ë O
ér ( êm ë O
Fr )ùú=ån
k û k=1
Fr )ùú=ån
k û k=1
Fr )ùú=ån
k û k=1
( r ) =
mx Fk 0;
( r ) =
my Fk 0;
( r ) =
mz Fk 0.
105
Таким образом, если твёрдое тело находится в равновесии под действием произвольной системы сил, то для неё можно составить шесть уравнений
равновесия: |
|
r |
n |
n |
|
å Fkx =0; |
å mx (Fk ) =0; |
|
k=1 |
k=1 |
r |
n |
n |
|
å Fky =0; |
å my (Fk ) =0; |
|
k=1 |
k=1 |
r |
n |
n |
|
å Fkz =0; |
å mz (Fk ) =0. |
|
k=1 |
k=1 |
|
106
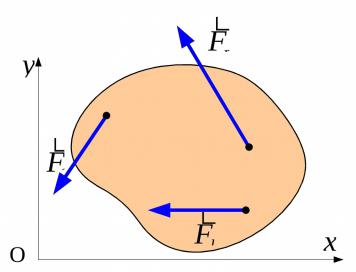
5.5. Уравнения равновесия плоской произвольной системы сил
Система сил, линии действия которых расположены произвольно в одной плоскости, называется плоской произвольной.
107
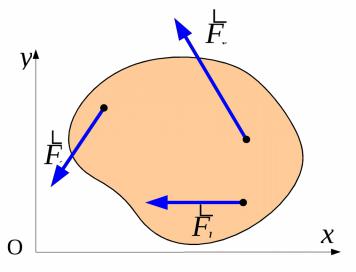
Плоская произвольная система сил является частным случаем пространственной произвольной системы сил.
Запишем уравнения равновесия пространственной произвольной системы сил и выберем из них уравнения, соответствующие плоской произвольной системе
сил. |
n |
n |
r |
|
å Fkx =0; |
å mx (Fk ) =0; |
|
|
k=1 |
k=1 |
r |
|
n |
n |
|
|
å Fky =0; |
å my (Fk ) =0; |
|
|
k=1 |
k=1 |
r |
|
n |
n |
|
|
å Fkz =0; |
å mz (Fk ) =0. |
|
|
k=1 |
k=1 |
108 |
Таким образом, если твёрдое тело находится в равновесии под действием плоской произвольной системы сил, то для неё можно составить три уравнения равновесия:
n |
kx |
|
n |
|
n |
O ( |
r |
|
) å |
=0; |
å ky |
=0; |
å |
k ) |
=0. |
||
1 |
F |
F |
|
m F |
||||
k=1 |
|
|
k=1 |
|
k=1 |
|
|
|
Кроме этих уравнений для плоской произвольной системы сил можно получить следующие две формы
уравнений равновесия: |
|
r |
|
|
n |
r |
n |
n |
|
2) å mA (Fk ) =0; |
å mB (Fk ) =0; |
å Fkx =0. |
||
k=1 |
|
k=1 |
|
k=1 |
Здесь А, В – два произвольных центра; Ox – ось, не
перпендикулярная прямой AB.
109
Из представленных уравнений три уравнения для плоской произвольной системы сил являются
тождествами: |
n |
n |
r |
|
å Fkx =0; |
å mx (Fk ) º 0; |
|
|
k=1 |
k=1 |
r |
|
n |
n |
|
|
å Fky =0; |
å my (Fk ) º 0; |
|
|
k=1 |
k=1 |
r |
|
n |
n |
|
|
å Fkz º 0; |
å mz (Fk ) =0. |
|
|
k=1 |
k=1 |
|
Так как на плоскости момент силы относительно
оси z совпадает по величине и по знаку с моментом силы относительно начала координат, то последнее
уравнение запишем в таком виде: |
|
|
n |
r |
|
å mO (Fk ) =0. |
110 |
|
k=1 |
|
|
) |
n |
|
A ( |
r |
|
n |
|
B ( |
r |
|
n |
C ( |
r |
|
å |
m |
k ) |
=0; |
å |
m |
k ) |
=0; |
å |
k ) |
=0. |
||||
3 |
k=1 |
|
F |
k=1 |
|
F |
k=1 |
m F |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь А, В, С – три произвольных центра, не лежащие на одной прямой.
111
6. Связи и силы реакций связей
Свободное тело – твёрдое, не закреплённое тело, которому можно сообщить любые перемещения в пространстве.
Несвободное тело – твёрдое тело, перемещения которого в пространстве ограничены другими телами, скреплёнными или соприкасающимися с ним.
Связи – тела, ограничивающие перемещения данного тела в пространстве.
Сила давления – сила, с которой тело действует на связь.
112
Сила реакции связи – сила, с которой связь дей- ствует на рассматриваемое тело.
Направление силы реакции связи. Сила реакции связи направлена противоположно тому направлению, в котором связь препятствует перемещению данного тела.
Активные силы – это силы, которые могут сообщить движение свободному телу.
Гладкая поверхность – это поверхность, трением со стороны которой можно пренебречь. Сила реакции гладкой поверхности направлена по общей нормали в точке контакта поверхностей соприкасающихся тел и
приложена в этой точке, рис. 44.
113
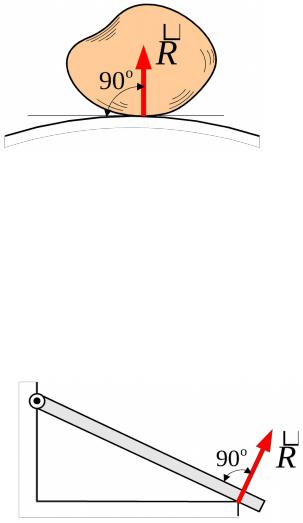
Рис. 44
Если гладкое тело опирается на ребро, то сила реакции направлена по нормали к поверхности тела, рис. 45.
Рис. 45
114
