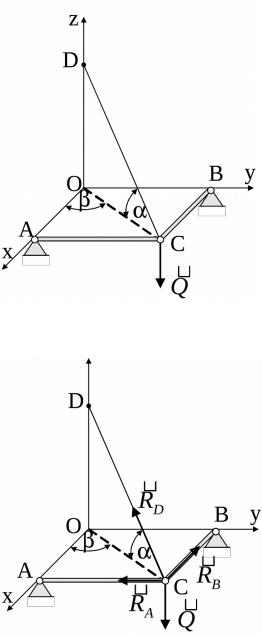
Пример 4. Определить натяжение цепи DC и усилия в стержнях АС и ВС, удерживающих груз Q, если стержни взаимно перпендикулярные и лежат в горизонтальной плоскости. Известно, что АС = a , ВС = b, DC = d, рис.24.
1. Запишем краткое условие задачи и выполним рисунок.
Дано: а, в, d, Q. Определить: SCD, SCB, SCA. 2. Составим расчётную схему. Рассматри-
ваем равновесие узла С. На него действует заданная сила . Узел имеет три связи: невесо- мые стержни АС и ВС; гибкую нить (цепь) DC. На узел действуют силы реакций связей:
RA , RB , RD . рис. 25.
Введём систему координат Оxyz.
Рис. 24
Рис. 2542
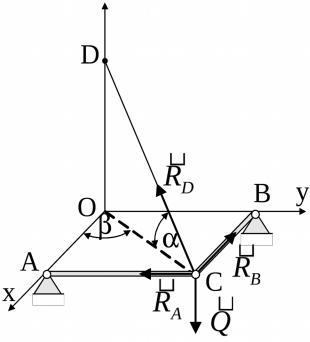
Рис. 25
Предварительно найдём проекции силы RD на оси х и y способом двойного проецирования:
RDx RD cos cos ; RDy RD cos sin .
43
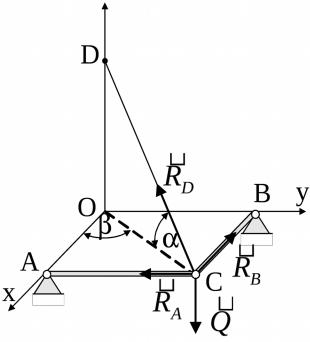
3. Система сил, действующих на узел С, – сходящаяся, поэтому составляем три уравнения равновесия:
n
Fkx RB RD cos cos 0;
k 1
n
Fky RA RD cos sin 0;
k 1
n
Fkz Q RD sin 0.
k 1
Рис. 25
4. Число уравнений соответствует числу неизвестных. Находим из уравнений неизвестные величины:
44
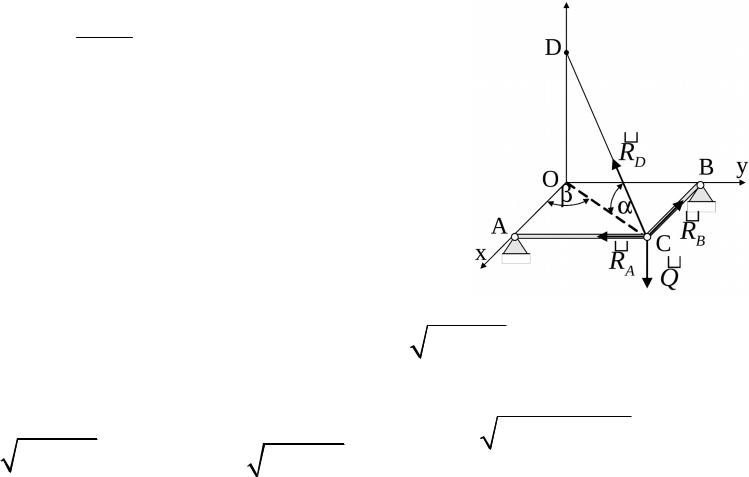
RD sinQ ;
RA RD cos sin ;
RB RD cos cos ;
Из рисунка найдём:
|
sin OD |
; |
cos |
a2 b2 |
|
; |
|
|
|
|
|
|||
|
d |
|
|
|
|
|
||||||||
|
a |
|
d |
|
b |
|
|
|
|
|
|
|
||
sin |
; |
cos |
; |
OD d |
2 |
b |
2 |
a |
2 |
. |
||||
a2 b2 |
|
|
|
|
||||||||||
a2 b2 |
|
|
|
|||||||||||
После подстановки тригонометрических выражений получим:
R |
d |
Q ; |
R |
b |
Q ; |
R |
|
|
a |
Q . |
|
|
A |
|
|||||||
D |
OD |
|
B |
OD |
|
|
|
OD |
45 |
|
|
|
|
|
|
|
|
Искомые усилия равны соответствующим реакциям:
SCD RD ; SCB RB ; SCA RA.
Знаки «минус» показывают, что истинные направления реакций стержней противоположны показанным на расчётной схеме, то есть, в данной задаче стержни не растянуты, а сжаты.
;Рекомендуется реакции стержней всегда строить от узла, предполагая, что все стержни растянуты. Знак подскажет вам,
;каково истинное состояние стержня.
.
46
Задание 4. Решить задачи 13 16, используя условия равновесия пространственной сходящейся системы сила.
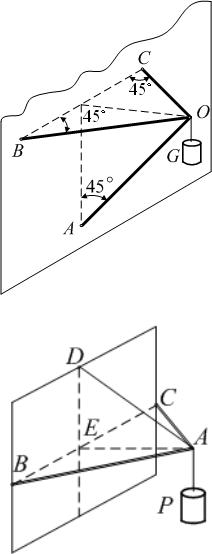
13. Груз G = 100 Н поддерживается брусом |
|
АО, шарнирно закреплённым в точке А и |
|
наклонённым под углом 45 к горизонту, и |
|
двумя горизонтальными цепями ВО и СО |
|
одинаковой длины; СВО = ВСО =45 . Найти |
|
усилие S в брусе и натяжения Т цепей, рис. 26. |
|
Ответ: S =-141 Н T = 71 Н |
Рис. 26 |
14.Найти усилия S1 и S2 в стержнях АВ и АС
иусилие Т в тросе АD, если дано, что СВА =
ВСА = 60 , ЕАD = 30 . Вес груза Р равен 300 Н. Плоскость АВС горизонтальна. Крепления стержней в точках А, В и С шарнирные, рис. 27.
Ответ: T =600 Н S1 = S2 -300 Н |
Рис. 2747 |
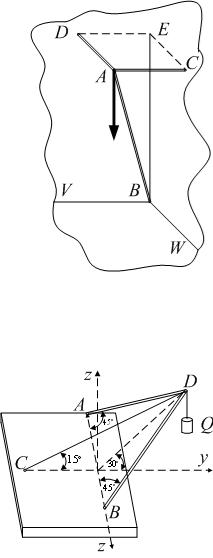
15. Найти усилия в стержне АВ и цепях АС и AD, удерживающих груз Q веса 420 Н, если АВ = 145 см, АС = 80 см, AD = 60 см, плоскость прямоугольника CADE горизонтальна, а плоскости V и W вертикальны. Крепление в точке В шарнирное, рис. 28.
Ответ: TC = 320 Н, TD = 2400 Н, TB = -580 Н. |
Рис. 28 |
|
16. Груз Q веса 1 кН подвешен в точке D, |
|
как указано на рисунке. Крепления стержней в |
|
точках А, В и D шарнирные. Определить |
|
реакции опор А, В и D, рис. 29. |
|
Ответ: RA = RB = 2,64 кН, RC = 3,35 кН. |
Рис. 29 |
48
КОНЕЦ
49