
- •ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
- •Содержание
- •1. Общие положения
- •Произвольная пространственная система сил может быть приведена к силе, равной главному вектору и
- •При равновесии тела под действием произвольной пространственной системы сил выполняются векторные
- •2. Момент силы относительно оси
- •Момент силы относительно оси равен нулю в следующих случаях:
- •1)строим плоскость, перпендикулярную оси, которая составляет с плоскостью угол ;
- •2) проецируем силу на эту плоскость;
- •3) из точки пересечения оси z с плоскостью (точка О) на линию действия
- •4) найдём величину момента силы относительно оси z;
- •5) определяем знак момента.
- •Пример 2. На вал с маховиком, радиус которого равен r (рис. 4), действует
- •Для определения момента силы относительно оси x построим проекцию вала и силы на
- •Проекция силы на плоскость zOy равна:
- •Чтобы определить момент рассматриваемой силы относительно оси y, построим проекцию вала и силы
- •Из рисунка видим, что плечом силы T является радиус маховика.
- •Чтобы найти момент силы относительно оси z, построим проекцию вала и силы на
- •Со стороны положительного направления оси z видим, что проекция силы стремится создать вращение
- •3. Тренировочные задания
- •Задание 2. Ось коленчатого вала (рис. 9) расположена вдоль оси x и удерживается
- •Построим вид вала с положительной стороны оси x.
- •4. Применение теоремы Вариньона
- •2. Момент данной силы определяется как алгебраическая сумма моментов каждой составляющей. Вполне возможно,
- •Сила P равна сумме двух составляющих
- •Таким образом, r
- •Таким образом, момент силы Pотносительно оси y равен:
- •5. Примеры решения задач
- •Рассмотрим примеры решения задач на равновесие тела под действием пространственной произвольной системы сил.
- •Определить силуQ , а также реакции подшипника В и сферического шарнира А, если
- •Решение
- •2. Какие активные силы приложены к валу?
- •3. Как называются связи, действующие на вал?
- •5. Как направлена сила реакции сферического шарнира A?
- •6. Как направлена сила реакции цилиндрического шарнира В?
- •7. Как называется система сил, действующая на вал AB?
- •8. Какие уравнения равновесия можно составить для прос- транственной произвольной системы сил?
- •Составьте первое уравнение:
- •Составьте четвёртое уравнение.
- •6.Задачи для самостоятельного решения
- •2. Коленчатый вал АВ расположен в горизонтальной плоскости. Имеет диск D, плоскость которого
- •3. Прямоугольная плита весом Р укреплена в горизонтальном положении с помощью шарнира А,
- •5. Горизонтальный вал АВ имеет два шкива С и D ремённой передачи, причём
- •КОНЕЦ
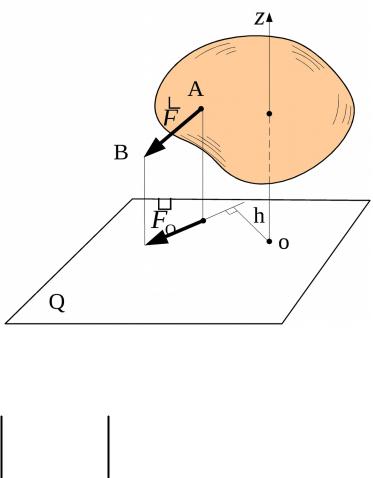
4) найдём величину момента силы относительно оси z;
|
|
Рис. 6 |
|
r |
|
FQh F cos |
|
mz F |
h. |
11
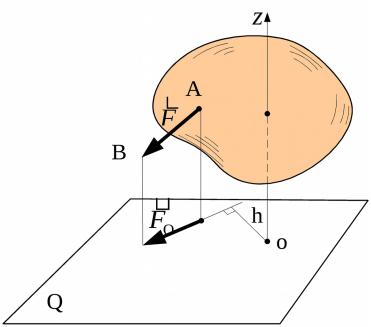
5) определяем знак момента.
Момента силы имеет знак (+), если с положительного конца оси поворот, который стремится совершить проекция силы на плоскость Q виден против часовой стрелки, и знак (-),если по ходу часовой стрелки. Следовательно момент силы на рис. 6 равен:
r |
FQh F cos |
|
mz F |
h. |
Рис. 6 |
12 |
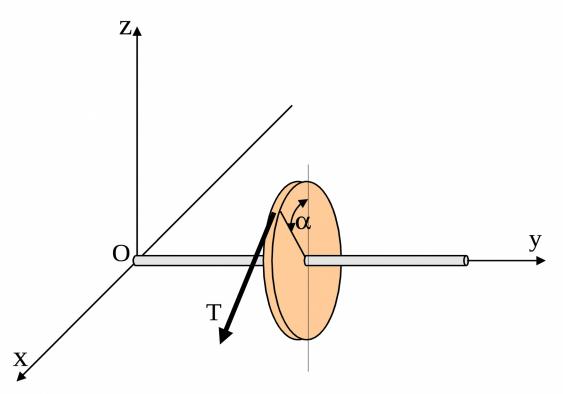
Пример 2. На вал с маховиком, радиус которого равен r (рис. 4), действует сила . Требуется определить моменты этой силы относительно каждой из координатных осей Oxyz.
Рис. 4
13
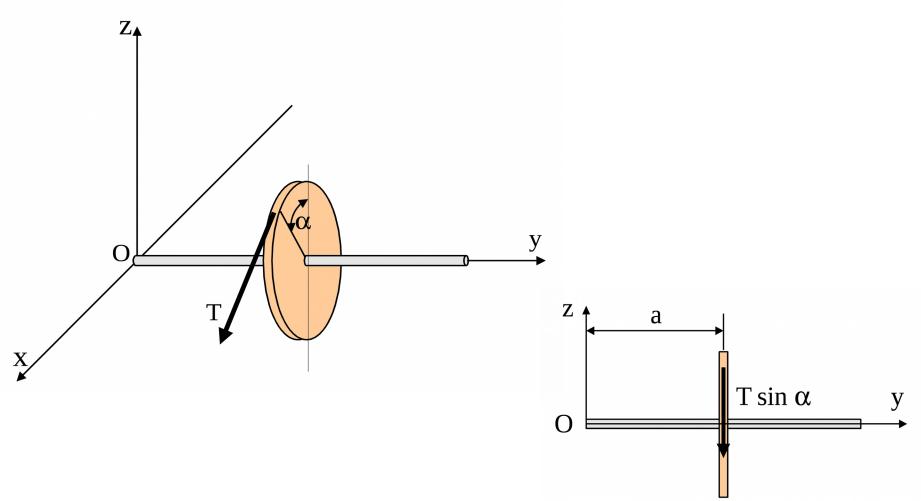
Для определения момента силы относительно оси x построим проекцию вала и силы на плоскость, перпендикуляр- ную этой оси, т. е. на плоскость zOy, рис. 5.
Рис. 4
Рис. 5
14
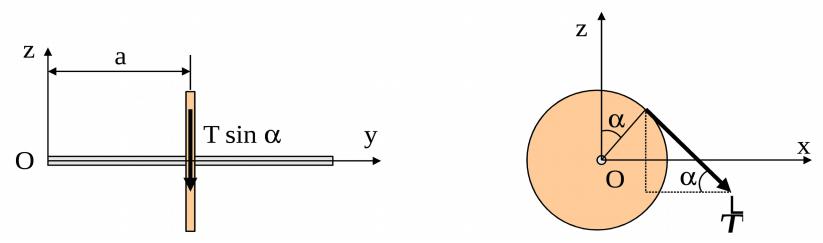
Проекция силы на плоскость zOy равна:
Тr' Тrsin
Из точки пересечения оси x с плоскостью (точка О) прове- дём плечо силы . Его величина совпадает с размером а.
Со стороны положительного направления оси x видим, что сила стремится вращать вал вокруг точки О по ходу часовой стрелки. Значит, момент силы относительно оси Оx имеет знак
(–). В результате момент силы относительно оси Оx равен:
mx T T sin a 15
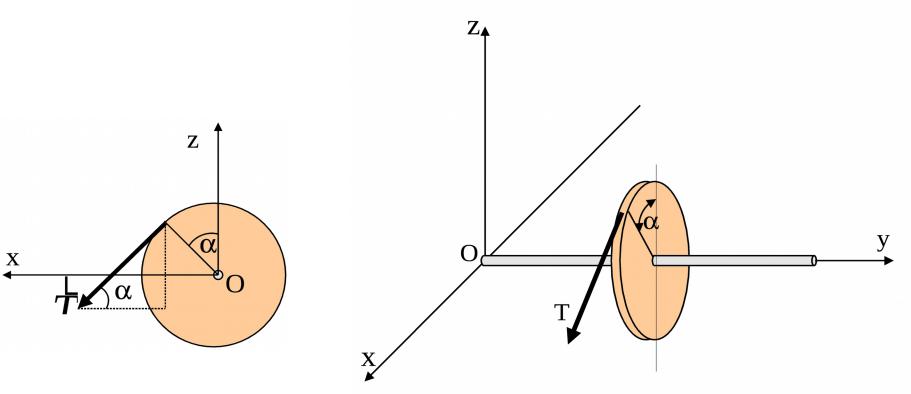
Чтобы определить момент рассматриваемой силы относительно оси y, построим проекцию вала и силы на плоскость, перпендикулярную оси Oy – плоскость xOz, рис. 6. Из точки пересечения оси Oy с этой плоскостью (точки О) на линию действия проекции силы восстановим перпендикуляр. По величине и направлению он совпадает с радиусом маховика при любом угле .
Рис. 6 |
Рис. 4 |
|
16
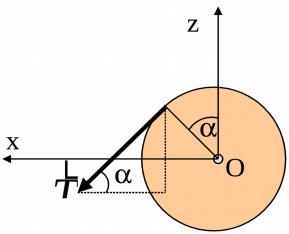
Из рисунка видим, что плечом силы T является радиус маховика.
Рис. 6
Со стороны положительного направления оси y видно, что проекция силы стремится создать вращение вала относительно точки О против хода часовой стрелки. Поэтому момент силы относительно оси y равен:
my T T r
17
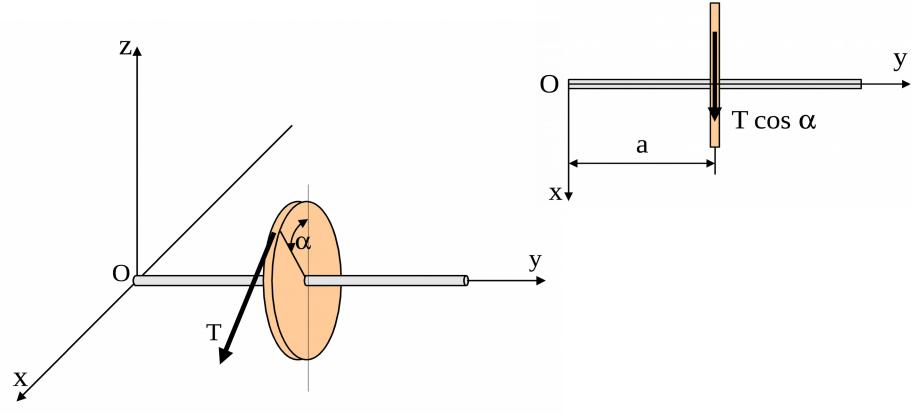
Чтобы найти момент силы относительно оси z, построим проекцию вала и силы на плоскость, перпендикулярную оси Oz
– плоскость xOy, рис. 7. Из точки пересечения оси Oz с этой плоскостью (точки О) на линию действия проекции силы восстановим перпендикуляр. По величине и направлению он совпадает с размером а.
Рис. 7
Рис. 4 |
18 |

Со стороны положительного направления оси z видим, что проекция силы стремится создать вращение вала относительно точки О по ходу часовой стрелки. Поэтому момент силы T относительно оси Oz имеет знак «–» и равен
mz Tr T cos a
19
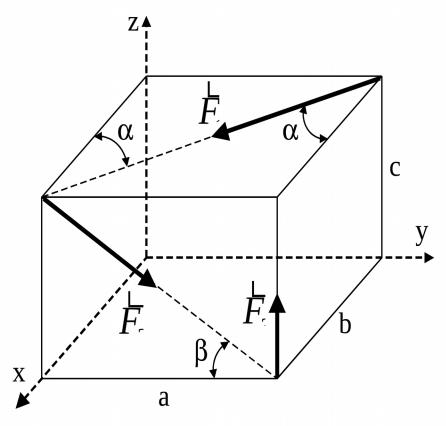
3. Тренировочные задания
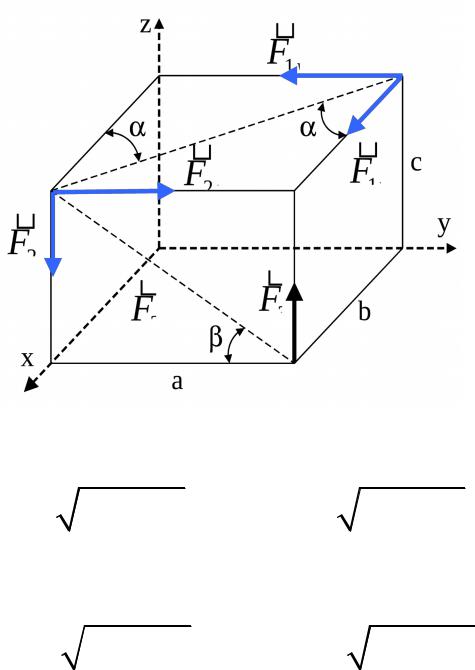
Задание 1. К параллелепипеду на рис. 8, стороны которого равны a, b и c, приложены силы . Значения углов , , заданы. Запишите моменты этих сил относительно осей x, y, z, и сравните свои результаты с правильными ответами, приведенными ниже.
Рис. 8 |
20 |
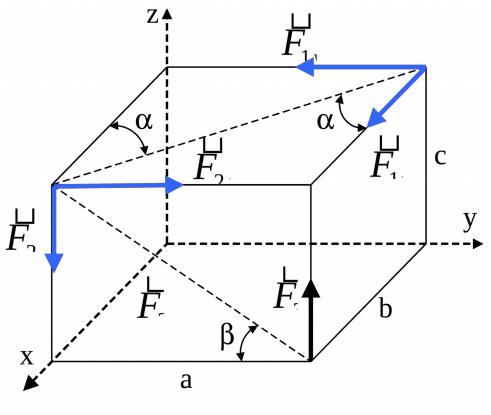
F1x F1 cos |
Рис. 8 |
|
mx |
||
F1y F1 sin |
||
my |
||
F2 у F2 cos |
||
F2 z F2 sin |
mz |
r
Fr1 Fr1 F1
F1 sin c;
F1 cos c;
F1 cos a;
21
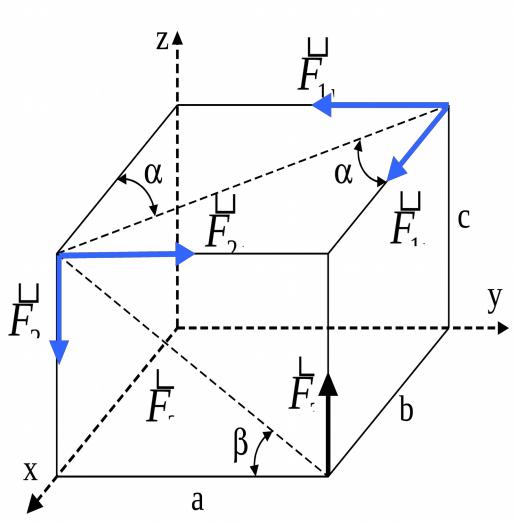
r |
F2 cos c; |
|
|
mx F2 |
|
||
r |
F2 |
|
Рис. 8 |
my F2 |
sin b; |
|
|
r |
F2 |
|
|
mz F2 |
cos b; |
22 |
|
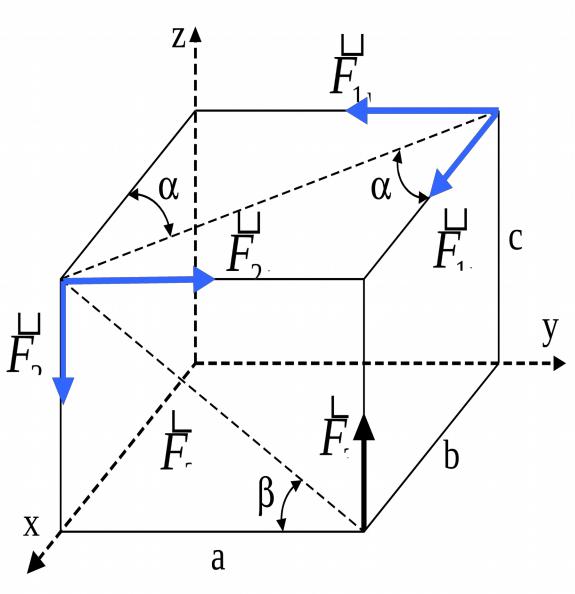
r |
F3 a; |
|
mx F3 |
|
|
r |
F3 b; |
|
my F3 |
|
|
r |
0. |
|
mz F3 |
Рис. 8 |
23
|
|
a |
Рис. 8 |
c |
|
|
|
||||
sin |
|
; |
sin |
|
; |
|
|||||
|
|
|
|
|
|
||||||
|
a2 b2 |
|
a2 c2 |
|
|||||||
cos |
|
b |
|
; |
cos |
a |
|
. |
|
||
|
a2 b2 |
|
a2 c2 |
|
24 |
||||||
