
- •Линейные пространства векторов. Скалярное произведение. Понятие базиса и линейной независимости элементов линейного пространства. Преобразования базиса.
- •Определение матрицы. Операции с матрицами (умножение на скаляр, сложение, умножение матриц, транспонирование матриц). Обратная матрица и методы ее получения. Функции от матриц.
- •Производные. Необходимое и достаточное условие дифференцируемости функции. Частные производные. Полный дифференциал. Производная и дифференциал сложной функции.
- •Градиент функции. Производные по направлению. Необходимые и достаточные условия экстремума функции многих переменных. Условные экстремумы. Метод множителей Лагранжа.
- •Задачи аппроксимации функций (интерполяция, экстраполяция, приближение в среднем). Способы построения интерполяционного полинома. Аппроксимации на основе ортогональных базисов. Понятие сплайна.
- •Численные методы оптимизации: методы Ньютона и секущей, методы покоординатного и градиентного спуска. Улучшение сходимости градиентных методов.
- •Численные методы оптимизации, основанные на случайных числах. Метод Монте-Карло, линейный случайный поиск, метод оптимизации отжигом.
- •Прямые и итерационные методы решения систем линейных алгебраических уравнений. Методы для систем с матрицами специального вида (ленточные, треугольные, положительно-определенные).
- •Линейные пространства функций (примеры). Скалярное произведение и норма. Операторы над линейными пространствами функций. Функционалы. Собственные числа и функции оператора в пространстве l2.
- •Определение вероятности. Вероятностная модель и вероятностное пространство. Вероятность случайного события и методы ее статистического оценивания по выборке.
- •Модель случайной величины. Закон, функция, плотность распределения. Квантили и моменты распределений, методы их статистического оценивания по выборке.
- •Вероятностные и толерантные интервалы: сходства и различия. Понятия точечного и интервального оценивания. Доверительные интервалы. Несмещенные и эффективные оценки.
- •Параметрическое оценивание распределений случайной величины. Метод моментов. Метод наибольшего правдоподобия и его численная реализация. Способы проверки качества параметрического оценивания.
- •Статистические гипотезы и статистические критерии. Односторонние и двусторонние критерии. Критерии согласия. Параметрические критерии. Ошибки первого и второго рода. Мощность критерия.
- •Модель многомерной случайной величины. Совместные и условные распределения. Условные моменты распределений и их оценивание по выборке. Многомерное распределение Гаусса и его свойства.
- •Случайные процессы и временные ряды. Понятие стационарности. Ковариационная (корреляционная функция). Теорема Карунена-Лоэва. Спектральная плотность случайных процессов.
- •Алгоритмы на графах. Алгоритмы обхода (поиска на) графах. Обнаружение кратчайшего пути и минимального цикла в графе. Построение остовного дерева.
- •Основные понятия машинного обучения. Отличие машинного обучения от статистики. Методы на обучении с учителем. Методы на обучении без учителя. Метрики качества алгоритмов машинного обучения.
- •Цикл обучения. Понятия обучающей и тестовой выборки. Отложенная выборка. Кросс-валидация. Понятия недообучения и переобучения. Дилемма смещения и разброса. Размерность Вапника-Червоненкиса.
- •Понятия классификации и кластеризации. Метрические, иерархические, вероятностные методы классификации и кластеризации. Dbscan и kNn. Оценка качества классификации и кластеризации.
- •Понятие искусственной нейронной сети. Типы нейронных сетей. Понятие стохастического градиента для обучения нейронной сети. Многослойный перцептрон. Сверточные нейронные сети.
- •Методы снижения размерности данных. Метод главных компонент. Метод канонических корреляций. Методы факторного анализа. Нелинейные методы снижения размерности.
- •Принцип повышения размерности пространства. Метод опорных векторов. Понятие и свойства ядра. Метод Kernel-Trick.
- •Построение списка решений и дерева решений. Редукция деревьев решений. Понятие бэггинга и бустинга для деревьев решений. Случайный лес и способы его построения.
- •Обучение с подкреплением. Модели агентов и отклика среды. Задачи, решаемые обучением с подкреплением.
- •Ассоциативный анализ и задача о "покупательской корзине". Алгоритмы аprior и fp-Growth.
- •Способы представления знаний. Модели графов знаний. Полнота графов знаний. Методы прямого и обратного вывода по графам знаний. Онтологическая модель и средства ее реализации.
- •Экспертные методы в принятии решений. Принятие решений при многих критериях. Множество Парето. Экспертные системы поддержки принятия решений.
- •Методы машинного обучения для анализа текстовой информации. Понятие эмбеддинга. Методы построения и использования эмбеддингов при работе с текстом.
- •Генеративные методы машинного обучения. Генеративно-состязательные сети. Вариационные автокодировщики. Байесовские сети. Принципы работы, оценка качества.
Определение вероятности. Вероятностная модель и вероятностное пространство. Вероятность случайного события и методы ее статистического оценивания по выборке.
Определение вероятности. Вероятность – это численная мера предопределенности наступления события. Обычно она представлена в виде значения от 0 до 1, где 0 – означает, что событие невозможно, а 1 – означает, что событие обязательно произойдет. Для любого события A вероятность A обозначается как P(A).
Вероятностная модель и вероятностное
пространство. Вероятностная модель
– это абстрактное математическое
представление случайного явления, в то
время как вероятностное пространство
– математическая конструкция, которая
определяет вероятности в рамках этой
модели и обозначается в виде тройки (Ω,
F, P), где Ω – пространство выборки, F –
набор событий (также называемый
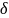 -алгеброй),
а P – функция вероятности.
-алгеброй),
а P – функция вероятности.
Пространство выборки – это множество всех возможных исходов случайного эксперимента. Например, если мы бросаем монету, то пространство выборки будет {"Орел", "Решка"}.
Событие – это подмножество пространства выборки. Оно представляет собой конкретный результат или набор результатов, событие A = {"Орел"}.
Пространство выборки и набор событий вместе образуют измеримое пространство, которое обеспечивает основу для определения вероятностей.
Функция вероятности присваивает значение вероятности каждому событию из набора событий в пространстве выборки. Она удовлетворяет следующим свойствам:
Неотрицательность: P(A) ≥ 0 для любого события A.
Аддитивность: если A и B – взаимоисключающие события (т.е. они не могут произойти одновременно), то P(A ∪ B) = P(A) + P(B).
Вероятность случайного события и методы ее статистического оценивания по выборке. Вероятность случайного события A – это вероятность того, что A произойдет. Она обозначается как P(A) и вычисляется с помощью функции вероятности, определенной на вероятностном пространстве. Вероятность события A может быть определена путем суммирования вероятностей всех исходов в A.
В статистике часто работают с выборками, чтобы сделать выводы о популяциях. Оценка вероятности события на основе выборки является важной задачей. Существует несколько методов статистического оценивания по выборке:
Классический метод. В этом методе вероятности оцениваются на основе теоретических моделей или предположений о базовой совокупности. Метод применим, когда события предположительно равновероятны:
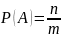
где
– число положительных исходов,
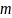 – число всех возможных исходов. Примером
использования классического метода
может быть расчет вероятности выпадения
1 из 6 значений на игральной кости.
– число всех возможных исходов. Примером
использования классического метода
может быть расчет вероятности выпадения
1 из 6 значений на игральной кости.
Эмпирический метод. Этот метод предполагает расчет относительной частоты события, происходящего в выборке. Формула эквивалентна предыдущей, но в отличие от нее в знаменателе стоит число
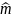 ,
отражающее общее число попыток, а в
числителе – число
,
отражающее общее число попыток, а в
числителе – число
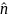 раз, когда желаемое событие произошло.
Иногда можно увидеть формулу, записанную
через предел:
раз, когда желаемое событие произошло.
Иногда можно увидеть формулу, записанную
через предел:
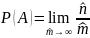
В ряде случае полезно будет оценить вероятностный интервал, основываясь на выборочной вероятности возникновения события.
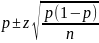
где
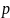 – оцененная по выборке вероятность
события,
– оцененная по выборке вероятность
события,
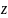 – табличное критическое значение для
нормального распределения с размером
выборки
,
соответствующая требуемому уровню
достоверности.
– табличное критическое значение для
нормального распределения с размером
выборки
,
соответствующая требуемому уровню
достоверности.
