
- •Линейные пространства векторов. Скалярное произведение. Понятие базиса и линейной независимости элементов линейного пространства. Преобразования базиса.
- •Определение матрицы. Операции с матрицами (умножение на скаляр, сложение, умножение матриц, транспонирование матриц). Обратная матрица и методы ее получения. Функции от матриц.
- •Производные. Необходимое и достаточное условие дифференцируемости функции. Частные производные. Полный дифференциал. Производная и дифференциал сложной функции.
- •Градиент функции. Производные по направлению. Необходимые и достаточные условия экстремума функции многих переменных. Условные экстремумы. Метод множителей Лагранжа.
- •Задачи аппроксимации функций (интерполяция, экстраполяция, приближение в среднем). Способы построения интерполяционного полинома. Аппроксимации на основе ортогональных базисов. Понятие сплайна.
- •Численные методы оптимизации: методы Ньютона и секущей, методы покоординатного и градиентного спуска. Улучшение сходимости градиентных методов.
- •Численные методы оптимизации, основанные на случайных числах. Метод Монте-Карло, линейный случайный поиск, метод оптимизации отжигом.
- •Прямые и итерационные методы решения систем линейных алгебраических уравнений. Методы для систем с матрицами специального вида (ленточные, треугольные, положительно-определенные).
- •Линейные пространства функций (примеры). Скалярное произведение и норма. Операторы над линейными пространствами функций. Функционалы. Собственные числа и функции оператора в пространстве l2.
- •Определение вероятности. Вероятностная модель и вероятностное пространство. Вероятность случайного события и методы ее статистического оценивания по выборке.
- •Модель случайной величины. Закон, функция, плотность распределения. Квантили и моменты распределений, методы их статистического оценивания по выборке.
- •Вероятностные и толерантные интервалы: сходства и различия. Понятия точечного и интервального оценивания. Доверительные интервалы. Несмещенные и эффективные оценки.
- •Параметрическое оценивание распределений случайной величины. Метод моментов. Метод наибольшего правдоподобия и его численная реализация. Способы проверки качества параметрического оценивания.
- •Статистические гипотезы и статистические критерии. Односторонние и двусторонние критерии. Критерии согласия. Параметрические критерии. Ошибки первого и второго рода. Мощность критерия.
- •Модель многомерной случайной величины. Совместные и условные распределения. Условные моменты распределений и их оценивание по выборке. Многомерное распределение Гаусса и его свойства.
- •Случайные процессы и временные ряды. Понятие стационарности. Ковариационная (корреляционная функция). Теорема Карунена-Лоэва. Спектральная плотность случайных процессов.
- •Алгоритмы на графах. Алгоритмы обхода (поиска на) графах. Обнаружение кратчайшего пути и минимального цикла в графе. Построение остовного дерева.
- •Основные понятия машинного обучения. Отличие машинного обучения от статистики. Методы на обучении с учителем. Методы на обучении без учителя. Метрики качества алгоритмов машинного обучения.
- •Цикл обучения. Понятия обучающей и тестовой выборки. Отложенная выборка. Кросс-валидация. Понятия недообучения и переобучения. Дилемма смещения и разброса. Размерность Вапника-Червоненкиса.
- •Понятия классификации и кластеризации. Метрические, иерархические, вероятностные методы классификации и кластеризации. Dbscan и kNn. Оценка качества классификации и кластеризации.
- •Понятие искусственной нейронной сети. Типы нейронных сетей. Понятие стохастического градиента для обучения нейронной сети. Многослойный перцептрон. Сверточные нейронные сети.
- •Методы снижения размерности данных. Метод главных компонент. Метод канонических корреляций. Методы факторного анализа. Нелинейные методы снижения размерности.
- •Принцип повышения размерности пространства. Метод опорных векторов. Понятие и свойства ядра. Метод Kernel-Trick.
- •Построение списка решений и дерева решений. Редукция деревьев решений. Понятие бэггинга и бустинга для деревьев решений. Случайный лес и способы его построения.
- •Обучение с подкреплением. Модели агентов и отклика среды. Задачи, решаемые обучением с подкреплением.
- •Ассоциативный анализ и задача о "покупательской корзине". Алгоритмы аprior и fp-Growth.
- •Способы представления знаний. Модели графов знаний. Полнота графов знаний. Методы прямого и обратного вывода по графам знаний. Онтологическая модель и средства ее реализации.
- •Экспертные методы в принятии решений. Принятие решений при многих критериях. Множество Парето. Экспертные системы поддержки принятия решений.
- •Методы машинного обучения для анализа текстовой информации. Понятие эмбеддинга. Методы построения и использования эмбеддингов при работе с текстом.
- •Генеративные методы машинного обучения. Генеративно-состязательные сети. Вариационные автокодировщики. Байесовские сети. Принципы работы, оценка качества.
Линейные пространства функций (примеры). Скалярное произведение и норма. Операторы над линейными пространствами функций. Функционалы. Собственные числа и функции оператора в пространстве l2.
Линейные пространства функций (примеры). Линейное пространство функций, также известное как векторное пространство функций, – это набор функций, удовлетворяющих определенным свойствам линейности.
Формальное определение. Пусть дано
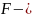 поле (реальных или комплексных чисел)
и некоторое множество
.
Тогда пространством линейных функций
по полю
поле (реальных или комплексных чисел)
и некоторое множество
.
Тогда пространством линейных функций
по полю
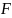 на множестве
называется множество всех функций
на множестве
называется множество всех функций
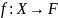 ,
определенных на заданной области
,
которое удовлетворяет следующим
свойствам:
,
определенных на заданной области
,
которое удовлетворяет следующим
свойствам:
1) Замкнутость при сложении. Для любых
двух функций
и
в
,
их сумма
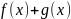 также находится в
.
также находится в
.
2) Замкнутость при скалярном умножении.
Для любой функции
в
и любого скаляра
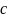 произведение
произведение
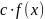 также находится в
.
также находится в
.
Примеры пространств линейных функций:
1) Пространство полиномов. Множество
всех многочленов с коэффициентами из
данного поля образует пространство
линейных функций. Например, пространство
всех многочленов степени не выше n,
обозначаемое как
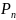 ,
является пространством линейных функций.
,
является пространством линейных функций.
2) Тригонометрическое пространство.
Множество всех периодических функций,
которые могут быть выражены в виде
конечной суммы функций синуса и косинуса,
образует пространство линейных функций.
Это пространство часто обозначается
как
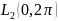 ,
представляя собой квадратично-непрерывные
функции на интервале
,
представляя собой квадратично-непрерывные
функции на интервале
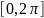 .
.
3) Пространство функций. Множество
всех непрерывных, дифференцируемых и
интегрируемых функций, определенных
на замкнутом интервале
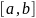 ,
образует пространство линейных функций.
Это пространство обозначается как
,
образует пространство линейных функций.
Это пространство обозначается как
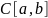 .
.
Свойства пространств линейных функций:
1) Нулевая функция. Каждое пространство линейных функций содержит нулевую функцию, которая отображает каждую точку области в нуль.
2) Аддитивность. Для любой функции
в пространстве линейных функций
существует другая функция
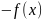 так, что
так, что
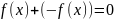 .
.
3) Замкнутость по линейным комбинациям. Линейное пространство функций замкнуто по линейным комбинациям, что означает, что любая конечная сумма функций в пространстве, умноженных на скаляры, также находится в этом пространстве.
4) Линейная независимость. Набор функций в линейном пространстве функций линейно независим, если ни одна функция из этого набора не может быть выражена в виде линейной комбинации остальных.
5) Базис и размерность. Базис для пространства линейных функций – это набор линейно независимых функций, которые охватывают все пространство. Размерность пространства – это количество функций в его базисе.
Операции над пространствами линейных функций:
1) Сложение. Две функции
и
в пространстве линейных функций могут
быть добавлены путем точечного сложения
их значений так, что
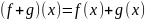 .
.
2) Умножение на скаляр. Функция
в линейном пространстве функций может
быть умножена на скаляр
путем умножения ее значений в каждой
точке на
,
так что
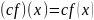 .
.
Скалярное произведение и норма. В контексте пространств линейных функций точечное произведение, также известное как скалярное умножение, и норма – важные понятия, которые помогают измерить связь между функциями и обеспечивают дополнительную структуру пространства.
Скалярное произведение, обозначаемое
как
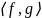 ,
– это бинарная операция, определенная
на пространстве линейных функций,
которая объединяет две функции и дает
скалярное значение. Она определяется
как интеграл произведения двух функций
по области
:
,
– это бинарная операция, определенная
на пространстве линейных функций,
которая объединяет две функции и дает
скалярное значение. Она определяется
как интеграл произведения двух функций
по области
:
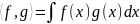 .
.
Скалярное произведение удовлетворяет следующим свойствам:
1) Линейность. Для любых функций
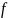 ,
,
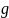 и
и
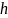 в пространстве линейных функций и любых
скаляров
в пространстве линейных функций и любых
скаляров
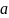 и
верно следующее:
и
верно следующее: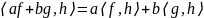 .
.
2) Симметрия. Точечное произведение
симметрично:
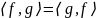 .
.
3) Положительная определенность. Если
– ненулевая функция, то
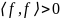 .
.
Норма функции
в пространстве линейных функций – это
мера ее длины или величины. Она обозначается
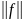 и определяется как квадратный корень
из скалярного произведения функции на
саму себя:
и определяется как квадратный корень
из скалярного произведения функции на
саму себя:
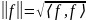 .
.
Норма удовлетворяет следующим свойствам:
1) Неотрицательность. Норма функции
всегда неотрицательна:
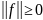 .
.
2) Нулевая норма. Норма нулевой функции
равна нулю:
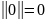 .
.
3) Однородность. Для любого скаляра
справедливо следующее выражение:
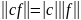 .
.
4) Неравенство треугольника. Для любых
функций
и
справедливо следующее выражение:
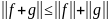 .
.
Скалярное произведение и норма дают возможность измерить сходство или несходство между функциями в линейном пространстве функций. Они также позволяют определить такие понятия, как ортогональность и расстояние.
Операторы над линейными пространствами
функций. Оператор
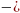 это функция, которая отображает элементы
из одного линейного пространства функций
в другое.
это функция, которая отображает элементы
из одного линейного пространства функций
в другое.
Формальное определение. Пусть
и
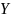 – линейные пространства функций по
полю
,
определенные на множествах
и
соответственно. Тогда оператором
– линейные пространства функций по
полю
,
определенные на множествах
и
соответственно. Тогда оператором
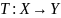 является функция, которая сопоставляет
каждой функции
в
единственную функцию
является функция, которая сопоставляет
каждой функции
в
единственную функцию
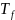 в
.
в
.
Операторы могут быть разбиты на категории относительно своих свойств и поведения: линейные операторы, операторы с ограниченной нормой, дифференциальные и интегральные операторы.
Свойства операторов:
1) Линейность. Линейные операторы
сохраняют линейность, то есть они
удовлетворяют
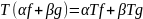 для любых функций
,
в линейном пространстве
и любых скаляров
,
для любых функций
,
в линейном пространстве
и любых скаляров
,
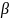 .
.
2) Композиция. Операторы могут быть
составлены, то есть композиция двух
операторов T и S представляет собой новый
оператор, определяемый как
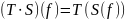 .
.
3) Инвертируемость. Некоторые операторы
имеют обратные операторы, то есть
существует оператор
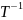 такой, что
такой, что
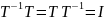 ,
где
оператор тождества. Инвертируемые
операторы играют важную роль при решении
уравнений с участием операторов.
,
где
оператор тождества. Инвертируемые
операторы играют важную роль при решении
уравнений с участием операторов.
4) Спектр. Спектр оператора
это множество всех комплексных чисел
,
для которых оператор
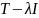 не является инвертируемым. Спектр дает
важную информацию о поведении и свойствах
оператора.
не является инвертируемым. Спектр дает
важную информацию о поведении и свойствах
оператора.
Операторы используются в обработке сигналов для анализа. Примеры включают оператор дифференцирования, преобразования Фурье, вейвлет-преобразования.
Функционалы. Функционал это отображение из линейного пространства функций в его базовое поле. Можно также услышать следующую формулировку: функционалы это линейные преобразования, которые возвращают скаляр, используя функцию в качестве входного параметра, например, интегрирование.
Свойства функционалов:
1) Линейность. Функционалы сохраняют
линейность, а значит удовлетворяют
таким свойствам, как аддитивность:
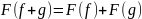 и однородность:
и однородность:
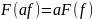 .
.
2) Непрерывность. Функционалы также
могут обладать свойствами непрерывности.
Считается, что функционал F является
непрерывным, если для любой последовательности
функций
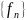 ,
сходящихся к функции
,
последовательность функционалов
,
сходящихся к функции
,
последовательность функционалов
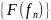 сходится к
сходится к
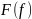 .
Это свойство гарантирует, что небольшие
изменения во входной функции приводят
к небольшим изменениям в выходном
скаляре.
.
Это свойство гарантирует, что небольшие
изменения во входной функции приводят
к небольшим изменениям в выходном
скаляре.
3) Норма. Функционалы могут быть использованы для определения норм на пространстве функций. Норма это математическое понятие, которое измеряет длину или размер вектора или, в данном случае, функции. Функционалы могут определять нормы, присваивая неотрицательное скалярное значение каждой функции в пространстве, удовлетворяющее таким свойствам, как позитивность, однородность и неравенство треугольника.
4) Двойственное пространство. Функционалы в линейных пространствах функций порождают понятие двойственного пространства. Двойственное пространство пространства функций состоит из всех возможных функционалов на этом пространстве. Оно само образует векторное пространство, в котором сложение и скалярное умножение определены точечно.
5) Внутреннее произведение. В некоторых случаях функционалы могут быть определены как внутренние произведения функций. Внутреннее произведение это обобщение точечного произведения для векторов, и оно измеряет сходство или ортогональность между двумя функциями. Внутренние произведения могут обеспечить дополнительную структуру и свойства пространства функций.
Собственные числа и функции оператора
в пространстве L2.
В Евклидовом пространстве
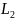 мы можем изучать собственные значения
и собственные функции операторов.
Собственное значение
оператора
мы можем изучать собственные значения
и собственные функции операторов.
Собственное значение
оператора
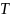 это скаляр, такой, что существует
ненулевая функция
в пространстве
,
удовлетворяющая
это скаляр, такой, что существует
ненулевая функция
в пространстве
,
удовлетворяющая
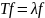 .
Соответствующая функция
называется собственной функцией.
.
Соответствующая функция
называется собственной функцией.
