9. Численные методы оптимизации, основанные на случайных числах. Метод Монте-Карло, линейный случайный поиск, метод оптимизации отжигом.

Методы оптимизации, основанные на случайных числах. Методы численной оптимизации на основе случайных чисел используются для поиска оптимального решения задачи путем случайного перебора пространства решений. Эти методы особенно полезны, когда пространство решений велико и сложно, а традиционные методы оптимизации неэффективны / невозможны.

Метод Монте-Карло, линейный случайный поиск, метод оптимизации отжигом.

Метод Монте-Карло¹ – это метод численной оптимизации, который использует случайную выборку для оценки решения проблемы. Он предполагает создание большого количества случайных выборок из пространства решений и использование статистического анализа для оценки оптимального решения.

В частности, простейшая реализация подразумевает создание случайной выборки из значений переменной, которую нужно оптимизировать, расчет целевой функции ошибок на этой выборке и выбор того значения, для которого функция ошибок окажется ниже.

Выборка по значимости – оптимизирует описанную выше процедуру случайного выбора значений таким образом, чтобы числа, лежащие ближе к ожидаемому минимуму функции потерь , выбирались чаще прочих. Т.е. вместо равномерного распределения требуется подобрать такое 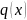, чтобы ожидаемое значение функции потерь сошлось к минимуму быстрее.

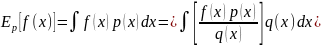
Выражение можно переписать как: . Индекс при означает, что все значения случайной переменной отныне выбираются согласно функции плотности распределения .

Марковская цепь Мотне-Карло и, в частности, реализация, предложенная Метрополисом и Гастингсом, представляет собой еще один алгоритм оптимизации параметров функции потерь, использующий цепи Маркова для генерации последовательности значений параметров, которые выбираются из заданного вероятностного распределения.

Алгоритм Метрополиса-Гастингса:

1. Выбрать начальное значение параметра .

2. Для каждой эпохи работы алгоритма, т.е. для каждого :

а) Сгенерировать новое значение параметра , основываясь на произвольно заданном распределении, в общем случае это может быть Гауссово (нормальное) распределение вероятностей со средним в точке .

б) Рассчитать коэффициент принятия решения α как , где и по сути являются аналогами марковских вероятностей перехода в новое состояние и сохранения текущего состояния, соответственно. Получившееся отношение пропорционально , где – целевая функция плотности распределения случайной величины. Для решения задачи минимизации функции ошибок, целевой функцией плотности распределения можно считать функцию правдоподобия получения наблюдаемых данных при заданных параметрах.

в) Рассчитать значение µ, лежащее в диапазоне от 0 до 1, исходя из равномерного распределения вероятностей.

г) Если , то новое значение принимается, в противном случае остается неизменным.

3. Цикл продолжается до тех пор, пока не будет достигнуто заданное число эпох или же пока не будет достигнуто определенное значение точности. Отметим и то, что первые 20% значений обычно отрезаются, т.к. цепи нужно время, чтобы установиться в стационарный режим работы.

Финальным результатом будет среднее или мода всех получившихся в результате блуждания марковской цепи значений .

Линейный случайный поиск – это алгоритм численной оптимизации, целью которого является нахождение минимума или максимума функции путем итеративного исследования пространства поиска в случайном порядке. Это простой и понятный метод, который не требует информации о градиенте оптимизируемой функции. Основные этапы линейного случайного поиска:

1. Пространство поиска. Алгоритм работает в заранее определенном пространстве поиска, которое обычно определяется верхней и нижней границами для каждого оптимизируемого параметра или переменной.

2. Инициализация. Алгоритм начинает работу со случайной инициализации точки в пространстве поиска. Эта начальная точка служит отправной точкой для процесса оптимизации.

3. Оценка. Функция потерь, подлежащая оптимизации, оценивается в текущей точке пространства поиска. Значение функции потерь в этой точке используется в качестве эталона для сравнения с будущими оценками.

4. Возмущение. Случайные возмущения применяются к текущей точке для создания новых точек-кандидатов в пространстве поиска. Эти возмущения обычно создаются путем добавления или вычитания небольшого случайного значения из каждого параметра или переменной.

5. Оценка и обновление. Функция потерь оценивается в каждой точке-кандидате, и, если точка-кандидат имеет лучшее значение, чем текущая точка, она становится новой текущей точкой. В противном случае текущая точка остается неизменной.

6. Итерация. Шаги 4 и 5 повторяются в течение заданного количества итераций или до тех пор, пока не будет достигнут критерий остановки. Критерий остановки может быть основан на количестве итераций, достижении определенного порогового значения функции или других критериях сходимости.

7. Выход. После завершения процесса оптимизации алгоритм возвращает конечную точку, которая достигла наилучшего значения функции в пространстве поиска.

Оптимизация отжига, является эвристическим алгоритмом, вдохновленным процессом отжига в металлургии. Он используется для нахождения глобального минимума или максимума функции путем итеративного вероятностного исследования пространства поиска. Оптимизация отжигом особенно эффективна для решения комбинаторных задач оптимизации. Основные этапы оптимизации с помощью отжига:

1. Пространство поиска. Алгоритм работает в заранее определенном пространстве поиска, которое обычно определяется верхней и нижней границами для каждого оптимизируемого параметра или переменной.

2. Инициализация. Алгоритм начинается со случайной инициализации точки в пространстве поиска. Эта начальная точка служит отправной точкой для процесса оптимизации.

3. Оценка. Функция потерь, подлежащая оптимизации, оценивается в текущей точке пространства поиска. Значение функции потерь в этой точке используется в качестве эталона для сравнения с будущими оценками.

4. Возмущение. Возмущения применяются к текущей точке для создания новых точек-кандидатов в пространстве поиска. Эти возмущения могут быть созданы путем добавления или вычитания небольшого случайного значения из каждого параметра или переменной, аналогично линейному случайному поиску.

5. Критерии приемлемости. В отличие от линейного случайного поиска, оптимизация отжига вводит критерий приемлемости, в частности Метрополиса, по распределению вероятностей Больцмана.

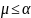, где равномерно распределена на

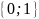
Критерии принятия определяет, будет ли точка-кандидат принята в качестве новой текущей точки или нет. Вероятность принятия худшей точки-кандидата уменьшается со временем согласно графику охлаждения, что позволяет алгоритму избежать локального оптимума.

6. График охлаждения. В оптимизации отжига используется график охлаждения, который контролирует скорость, с которой вероятность принятия уменьшается в течение итераций. График охлаждения обычно начинается с высокой температуры, которая позволяет больше исследовать, и постепенно снижает температуру к нулю, фокусируясь на эксплуатации.

7. Итерация. Шаги 4, 5 и 6 повторяются в течение заранее определенного количества итераций или до тех пор, пока не будет достигнут критерий остановки. Критерий остановки может быть основан на количестве итераций, достижении определенного порогового значения функции или других критериях сходимости.

8. Выход. После завершения процесса оптимизации алгоритм возвращает конечную точку, которая достигла наилучшего значения функции в пространстве поиска.

Все эти методы численной оптимизации, основанные на случайных числах, имеют свои преимущества и недостатки. Методы Монте-Карло требуют больших вычислительных затрат, но могут дать точные оценки оптимального решения. Линейный случайный поиск прост и легко реализуем, но может застрять в локальном оптимуме. Оптимизация отжигом эффективна при поиске глобального оптимума, но требует тщательной настройки параметров.

¹Метод Монте-Карло очень широкое понятие, которое, однако, начинается с простейшей оценки ожидаемого значения функции некоторой непрерывной или дискретной случайной величины аргумента. Распределение случайной величины может быть задано как функция плотности или же как таблица вероятностей того, что случайная переменная примет то или иное дискретное значение).

,