35. Генеративные методы машинного обучения. Генеративно-состязательные сети. Вариационные автокодировщики. Байесовские сети. Принципы работы, оценка качества.

Генеративные методы машинного обучения. Генеративные методы машинного обучения включают моделирование базового распределения данных и генерацию новых выборок из этого распределения. Двумя популярными генеративными методами являются генеративно-состязательные сети (GAN) и вариационные автоэнкодеры (VAEs), оба из которых имеют различные алгоритмы и принципы работы.

Генератоивно-состязательные сети (GAN). GAN состоят из двух нейронных сетей: генератора и дискриминатора. Генератор генерирует синтетические образцы, а дискриминатор различает реальные и сгенерированные образцы. Задача состоит в том, чтобы обучить обе сети одновременно, причем генератор должен научиться генерировать реалистичные образцы, которые могут обмануть дискриминатор.

Сеть-генератор принимает на вход вектор случайного шума и сопоставляет его со сгенерированным образцом с помощью функции 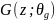, где 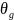представляет собой параметры генератора. Целью генератора является изучение базового распределения обучающих данных для генерации реалистичных образцов.

Сеть дискриминатора, обозначаемая как 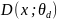, принимает на вход либо реальный образец , либо сгенерированный образец 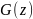и выдает вероятностную оценку, указывающую на то, является ли данный образец реальным или поддельным. Дискриминатор обучается таким образом, чтобы максимизировать вероятность правильной классификации реальных и сгенерированных образцов.

Процесс обучения заключается в итерационной оптимизации обеих сетей. Генератор пытается минимизиро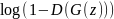вать , обманывая дискриминатор, чтобы тот классифицировал сгенерированные образцы как реальные. В то же время дискриминатор стремится максимизировать 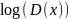для реальных образцов и для сгенерированных образцов.

Алгоритм GAN можно резюмировать следующим образом:

1. Инициализируйте сети генератора и дискриминатора случайными весами.

2. Обучите дискриминатор, предоставив ему реальные выборки из обучающих данных и сгенерированные выборки из генератора, пометив их как реальные или поддельные.

3. Обучите генератор, генерируя выборки и пропуская их через дискриминатор. Генератор предназначен для генерации выборок, которые дискриминатор классифицирует как реальные.

4. Повторите шаги 2 и 3, чтобы улучшить обе сети одновременно до достижения конвергенции.

Вариационные автокодировщики (VAEs). VAE – это генеративные модели, которые сочетают в себе элементы автоэнкодеров и вероятностного моделирования. Они нацелены на изучение сжатого представления входных данных, называемого скрытым пространством, которое может быть использовано для генерации новых выборок.

Сеть кодировщика, обозначаемая 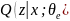, сопоставляет входные данные с латентным представлением . Она учится кодировать входные данные в вектор среднего значения и вектор стандартного отклонения , которые затем используются для выборки из гауссова распределения.

Сеть декодера, обозначаемая как 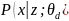, принимает латентное представление и восстанавливает исходные входные данные . Декодер стремится генерировать выборки, похожие на обучающие данные, путем обучения условному распределению .

Латентное пространство – это низкоразмерное представление входных данных. В процессе обучения используется трюк перепараметризации для выборки путем добавления случайного шума 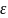к среднему и стандартному отклонению, полученному от кодера.

Алгоритм VAE можно резюмировать следующим образом:

1. Закодируйте входные данные в скрытое пространство меньшего размера с помощью сети кодировщиков.

2. Сделайте выборку из скрытого пространства для генерации скрытого вектора.

3. Декодируйте скрытый вектор с помощью сети декодеров для генерации восстановленного выходного сигнала.

4. Оптимизируйте модель, минимизируя потери при восстановлении и максимизируя член регуляризации, что побуждает скрытое пространство следовать предыдущему распределению (обычно гауссову распределению).

Байесовские сети. Байесовские сети – это вероятностные графические модели, которые представляют зависимости между переменными с использованием направленного ациклического графа. Они могут быть использованы для генеративного моделирования путем задания условных распределений вероятностей между переменными.

Узлы графа представляют переменные, а направленные ребра указывают на вероятностные зависимости. Каждому узлу соответствует условное распределение вероятности с учетом его родителей в графе.

Вывод в байесовских сетях заключается в вычислении апостериорных вероятностей на основе наблюдаемых данных. Это может быть сделано с помощью различных методов, таких как точные алгоритмы вычисления, например, Variable Elimination (VE), или приближенные методы, такие как выборка Марковской цепи Монте-Карло (MCMC).

Алгоритм байесовских сетей можно резюмировать следующим образом:

1. Определение структуры графика, представляющего переменные и их зависимости.

2. Присвоение условных распределений вероятностей каждой переменной на основе ее родительских значений на графике.

3. Выполнение вывода для вычисления вероятностей ненаблюдаемых переменных с учетом наблюдаемых переменных.

Оценка качества. Ниже приведены некоторые общие метрики оценки, которые помогают оценить разнообразие и качество сгенерированных выборок по сравнению с реальным распределением данных.

Оценка качества порождающе-состязательных сетей (GAN):

1. Начальный балл (IS). IS измеряет качество и разнообразие сгенерированных выборок путем оценки того, насколько хорошо они могут быть классифицированы с использованием начальной модели, обученной на реальных данных. Он объединяет среднюю вероятность класса и энтропию предсказанных вероятностей класса.

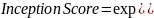
где 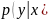– условное распределение классов для сгенерированной выборки ;

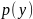– предельное распределение классов по всем сгенерированным выборкам;

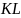– дивергенция Кульбака-Лейблера.

2. Начальное расстояние Фреше (FID). FID вычисляет расстояние между представлениями признаков реальных и сгенерированных выборок с использованием начальной модели. Он обеспечивает меру сходства между двумя распределениями и обычно используется в задачах генерации изображений.

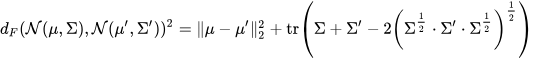
где и 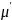– средние векторы признаков реальных и сгенерированных выборок;

и 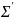– ковариационные матрицы реальных и сгенерированных выборок.

3. Расстояние Вассерштейна измеряет разницу между истинным распределением данных и сгенерированным распределением. Оно определяет, сколько "массы" необходимо перенести из одного распределения, чтобы преобразовать его в другое.

где и – истинное и сгенерированное распределения;

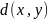– множество всех совместных распределений с маргинальными значениями и ;

– функция стоимости, измеряющая расхождение между и .

Оценка качества вариационных автокодировщиков (VAEs):

1. Потери при реконструкции определяют, насколько хорошо VAE может восстановить входные данные из латентного пространства. Обычно они рассчитываются с помощью средней квадратичной ошибки или бинарной кросс-энтропии между реконструированным выходом и исходным входом.

где 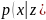– условное распределение входных данных с учетом латентного вектора .

2. Логарифмическая функция правдоподобия оценивает, насколько хорошо VAE отражает распределение обучающих данных. Более высокое значение функции правдоподобия указывает на лучшую производительность.

где – маргинальное распределение входных данных.

Оценка качества байесовских сетей сосредоточена на оценке их способности улавливать сложные зависимости между переменными и делать точные прогнозы.

1. Точность измеряет, насколько хорошо предсказания байесовской сети соответствуют истинным данным. При этом сравниваются предсказанные вероятности различных исходов с фактическими.

2. Способность байесовской сети улавливать сложные зависимости между переменными оценивается путем сравнения ее прогнозов с наблюдаемыми данными и оценки того, насколько хорошо она моделирует совместное распределение переменных.