
- •Линейные пространства векторов. Скалярное произведение. Понятие базиса и линейной независимости элементов линейного пространства. Преобразования базиса.
- •Определение матрицы. Операции с матрицами (умножение на скаляр, сложение, умножение матриц, транспонирование матриц). Обратная матрица и методы ее получения. Функции от матриц.
- •Производные. Необходимое и достаточное условие дифференцируемости функции. Частные производные. Полный дифференциал. Производная и дифференциал сложной функции.
- •Градиент функции. Производные по направлению. Необходимые и достаточные условия экстремума функции многих переменных. Условные экстремумы. Метод множителей Лагранжа.
- •Задачи аппроксимации функций (интерполяция, экстраполяция, приближение в среднем). Способы построения интерполяционного полинома. Аппроксимации на основе ортогональных базисов. Понятие сплайна.
- •Численные методы оптимизации: методы Ньютона и секущей, методы покоординатного и градиентного спуска. Улучшение сходимости градиентных методов.
- •Численные методы оптимизации, основанные на случайных числах. Метод Монте-Карло, линейный случайный поиск, метод оптимизации отжигом.
- •Прямые и итерационные методы решения систем линейных алгебраических уравнений. Методы для систем с матрицами специального вида (ленточные, треугольные, положительно-определенные).
- •Линейные пространства функций (примеры). Скалярное произведение и норма. Операторы над линейными пространствами функций. Функционалы. Собственные числа и функции оператора в пространстве l2.
- •Определение вероятности. Вероятностная модель и вероятностное пространство. Вероятность случайного события и методы ее статистического оценивания по выборке.
- •Модель случайной величины. Закон, функция, плотность распределения. Квантили и моменты распределений, методы их статистического оценивания по выборке.
- •Вероятностные и толерантные интервалы: сходства и различия. Понятия точечного и интервального оценивания. Доверительные интервалы. Несмещенные и эффективные оценки.
- •Параметрическое оценивание распределений случайной величины. Метод моментов. Метод наибольшего правдоподобия и его численная реализация. Способы проверки качества параметрического оценивания.
- •Статистические гипотезы и статистические критерии. Односторонние и двусторонние критерии. Критерии согласия. Параметрические критерии. Ошибки первого и второго рода. Мощность критерия.
- •Модель многомерной случайной величины. Совместные и условные распределения. Условные моменты распределений и их оценивание по выборке. Многомерное распределение Гаусса и его свойства.
- •Случайные процессы и временные ряды. Понятие стационарности. Ковариационная (корреляционная функция). Теорема Карунена-Лоэва. Спектральная плотность случайных процессов.
- •Алгоритмы на графах. Алгоритмы обхода (поиска на) графах. Обнаружение кратчайшего пути и минимального цикла в графе. Построение остовного дерева.
- •Основные понятия машинного обучения. Отличие машинного обучения от статистики. Методы на обучении с учителем. Методы на обучении без учителя. Метрики качества алгоритмов машинного обучения.
- •Цикл обучения. Понятия обучающей и тестовой выборки. Отложенная выборка. Кросс-валидация. Понятия недообучения и переобучения. Дилемма смещения и разброса. Размерность Вапника-Червоненкиса.
- •Понятия классификации и кластеризации. Метрические, иерархические, вероятностные методы классификации и кластеризации. Dbscan и kNn. Оценка качества классификации и кластеризации.
- •Понятие искусственной нейронной сети. Типы нейронных сетей. Понятие стохастического градиента для обучения нейронной сети. Многослойный перцептрон. Сверточные нейронные сети.
- •Методы снижения размерности данных. Метод главных компонент. Метод канонических корреляций. Методы факторного анализа. Нелинейные методы снижения размерности.
- •Принцип повышения размерности пространства. Метод опорных векторов. Понятие и свойства ядра. Метод Kernel-Trick.
- •Построение списка решений и дерева решений. Редукция деревьев решений. Понятие бэггинга и бустинга для деревьев решений. Случайный лес и способы его построения.
- •Обучение с подкреплением. Модели агентов и отклика среды. Задачи, решаемые обучением с подкреплением.
- •Ассоциативный анализ и задача о "покупательской корзине". Алгоритмы аprior и fp-Growth.
- •Способы представления знаний. Модели графов знаний. Полнота графов знаний. Методы прямого и обратного вывода по графам знаний. Онтологическая модель и средства ее реализации.
- •Экспертные методы в принятии решений. Принятие решений при многих критериях. Множество Парето. Экспертные системы поддержки принятия решений.
- •Методы машинного обучения для анализа текстовой информации. Понятие эмбеддинга. Методы построения и использования эмбеддингов при работе с текстом.
- •Генеративные методы машинного обучения. Генеративно-состязательные сети. Вариационные автокодировщики. Байесовские сети. Принципы работы, оценка качества.
Методы снижения размерности данных. Метод главных компонент. Метод канонических корреляций. Методы факторного анализа. Нелинейные методы снижения размерности.
Методы снижения размерности данных. Снижение размерности данных – это семейство методов, используемых в анализе и моделировании данных для уменьшения сложности данных при максимальном сохранении их исходной информативности. Это важнейший инструмент в науке о данных, особенно при работе с большими высокоразмерными наборами данных. К основным методам относятся анализ главных компонент (PCA), канонический корреляционный анализ (CCA), факторный анализ (FA) и нелинейные методы снижения размерности.
Метод главных компонент (Principal Component Analysis). PCA – это статистическая процедура, которая ортогонально преобразует исходные координаты набора данных в новый набор координат, называемых главными компонентами, которые отражают направление распространения вариации данных.
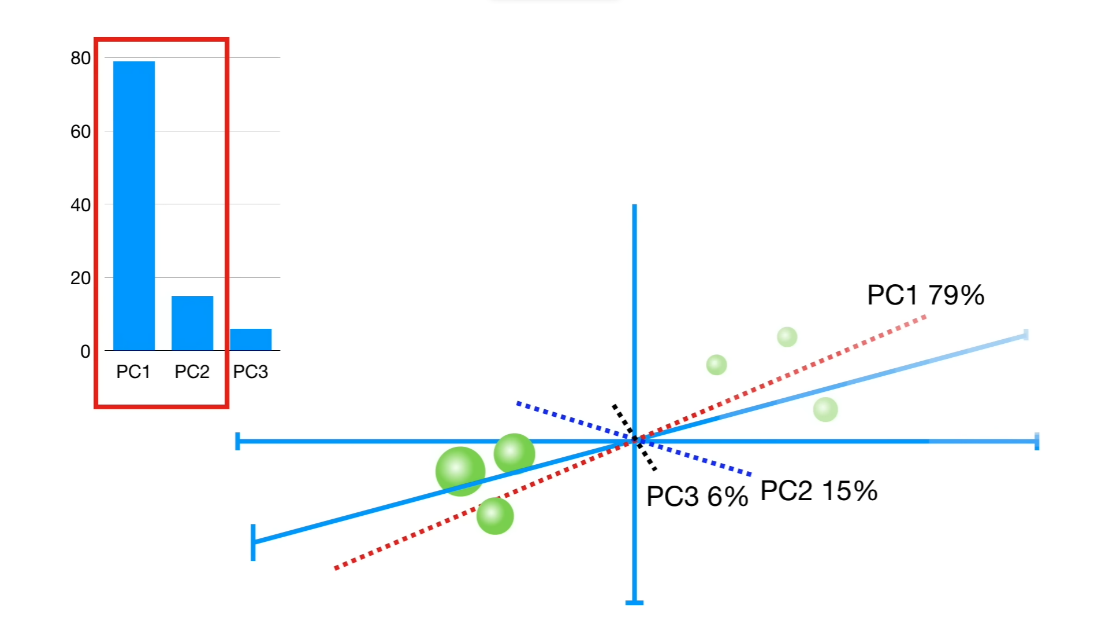
Основные этапы алгоритма:
Стандартизировать данные. Если предполагается использовать данные для обучения моделей, то и следует сохранить отдельно;
Вычислить ковариационную матрицу стандартизованных данных. Предполагается, что данные состоят из столбцов, отражающих признаки;
Вычислить собственные вектора и собственные значения ковариационной матрицы. Собственные вектора представляют собой главные компоненты, а соответствующие собственные значения – величину вариации, объясняемой каждой компонентой;
Выбрать желаемое количество главных компонент. Первая главная компонента учитывает наибольшую дисперсию данных, вторая компонента – вторую по величине дисперсию и так далее;
Спроецировать стандартизованные данные на выбранные главные компоненты, чтобы получить более низкоразмерное представление. Если данные используются для обучения моделей, то новые данные должны быть стандартизированы и затем преобразованы с использованием сохраненных значений и .
Метод канонических корреляций (Canonic Correlation Analysis). CCA – это метод, используемый для выявления и измерения ассоциаций между двумя наборами переменных. Он находит линейные комбинации переменных из каждого набора, которые максимально коррелируют друг с другом.
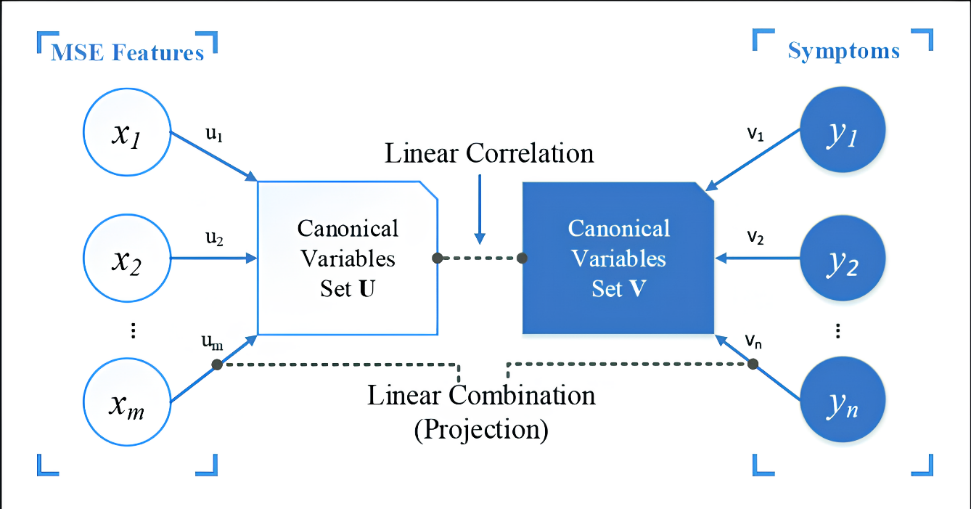
Основные этапы алгоритма:
Стандартизировать данные.
Рассчитать матрицы ковариаций для набора данных
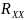 ,
,
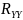 ,
а также их комбинации
,
а также их комбинации
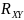 и
и
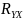 .
.Получить собственные числа и вектора для
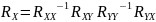 и, аналогично, для
и, аналогично, для
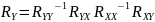 .
.Отсортировать получившиеся собственные вектора, образующие столбцы матриц
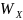 и
и
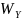 ,
в порядке убывания соответствующих им
собственных чисел.
,
в порядке убывания соответствующих им
собственных чисел.Чтобы посчитать каноничные переменные и необходимо умножить столбцы из набора на и на . Впрочем, обычно, достаточно получить лишь произведение набора переменных на коэффициенты первого столбца
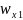 матрицы
:
матрицы
: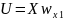 или, аналогично,
или, аналогично,
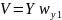 .Заметим,
что собственное число
.Заметим,
что собственное число
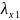 ,
соответствующее столбцу
,
будет также равно
,
соответствующее столбцу
,
будет также равно
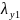 ,
а корень из него дает искомый коэффициент
корреляции Пирсона между
и
.
,
а корень из него дает искомый коэффициент
корреляции Пирсона между
и
.
Методы факторного анализа (Factor Analysis). FA – это статистический метод, используемый для объяснения изменчивости наблюдаемых коррелированных переменных в терминах потенциально меньшего числа ненаблюдаемых латентных переменных, называемых факторами. Снижение размерности происходит за счет анализа только тех переменных, которые имеют сильную корреляцию с выделенными факторами. Обычно, исключаются те переменные, что имеют исключительно низкую / высокую корреляцию одновременно со всеми факторами, т.к., вероятно, поведение этих переменных либо незначимо, либо наоборот свойственно всем наблюдениям, и потому имеет низкую дискриминирующую способность в рамках анализа.

Основные этапы алгоритма:
Предподготовка данных включает стандартизацию, проверку гипотез о нормальности совместного распределения, проверку на соответствие свойствам линейности. Часто используют критерий Кайзера-Мейера-Олкина или тест Бартлетта для проверки адекватности данных для целей факторного анализа. Тест Кайзера-Мейера-Олкина измеряет адекватность выборки путем изучения частичных корреляций между переменными, и значения выше 0,6 обычно считаются приемлемыми.
Выбор метода расчета факторов. Обычно предлагается на выбор метод главных компонент (PCA) или метод максимального правдоподобия (MLE).
При условии, что был выбран метод PCA, как и всегда, необходимо выбрать несколько PC, которые обычно выбирают по методу локтя, силуэта или просто все PC, для которых собственное число больше 1. Эти вектор-столбцы в дальнейшем будут называться факторами.
Для каждого фактора необходимо посчитать корреляцию с исходным набором признаков и построить таким образом факторную матрицу.
По факторной матрице рассчитать факторную нагрузку, которая отражает долю дисперсии исходных данных, которая может быть объяснена несколькими выбранными факторами. Для ее расчета достаточно возвести в квадрат полученные значения корреляции признака с каждым из факторов и сложить полученные значения.
Иногда, шаги 4 и 5 дополняют вращением факторной матрицы, например, методом varimax. Суть его работы сводится к тому, чтобы упростить вид исходной факторной матрицы так, чтобы один признак имел относительно высокую корреляцию с одним фактором и относительно низкую корреляцию со всеми остальными факторами.
Нелинейные методы снижения размерности. В то время как вышеперечисленные методы являются линейными, существует также несколько нелинейных методов снижения размерности. К ним относятся такие методы, как t-Distributed Stochastic Neighbor Embedding (t-SNE), Isomap и Locally Linear Embedding (LLE). Эти методы особенно полезны в тех случаях, когда структура данных не является линейной и включает сложные нелинейные связи. Они позволяют выявить глубинную структуру данных, сохраняя определенные связи в высокоразмерном пространстве при отображении в низкоразмерное.
