23. Понятия классификации и кластеризации. Метрические, иерархические, вероятностные методы классификации и кластеризации. Dbscan и kNn. Оценка качества классификации и кластеризации.

Понятия классификации и кластеризации. Классификация – это задача обучения с учителем, которая заключается в присвоении заранее определенных меток или категорий экземплярам данных на основе их признаков или атрибутов. Она стремится построить модель, которая может точно предсказывать класс невидимых экземпляров.

Кластеризация – это задача обучения без учителя, которая стремится группировать похожие экземпляры на основе их внутренних характеристик, без заранее определенных меток. Она помогает обнаружить скрытые закономерности или структуры в данных.

Метрические, иерархические, вероятностные методы классификации и кластеризации. Метрические методы основаны на измерении сходства или различия между экземплярами данных с использованием метрик расстояния. Общие метрики расстояния включают Евклидово расстояние, Манхэттенское расстояние и расстояние Минковского. Примеры алгоритмов классификации на основе метрик включают k-ближайших соседей (kNN) и метод опорных векторов (SVM).

Алгоритм kNN присваивает классовую метку новому экземпляру на основе голосования большинства его k ближайших соседей в пространстве признаков. Значение k определяет количество рассматриваемых соседей.

SVM ищет гиперплоскость, которая максимально отделяет точки разных классов друг от друга. Это делается путем нахождения опорных векторов – точек данных, ближайших к границе разделения. Гиперплоскость выбирается таким образом, чтобы максимизировать расстояние между опорными векторами и границей.

Иерархические методы создают иерархию кластеров путем итеративного объединения или разделения существующих кластеров на основе мер сходства. Два основных типа иерархической кластеризации – это агломеративная и дивизионная кластеризация.

Процесс агломеративной кластеризации начинается с каждого экземпляра как отдельного кластера и последовательно объединяет наиболее похожие кластеры до достижения критерия остановки. Результатом является дендрограмма, представляющая иерархическое отношение между экземплярами.

Процесс дивизионной кластеризации начинается с построения исходного кластера, содержащего все данные. Затем этот кластер разделяется на два подкластера, используя определенный алгоритм разделения, например, k-средних. После этого каждый из полученных подкластеров может быть рекурсивно разделен на более мелкие подкластеры до достижения заданного условия остановки.

Вероятностные методы используют статистические модели для оценки вероятности принадлежности экземпляра к каждому классу. Они делают предположения о распределении данных и оценивают параметры модели с использованием обучающих данных. Примеры вероятностных классификаторов включают наивный байесовский и логистическую регрессию.

Наивный байесовский алгоритм предполагает, что признаки условно независимы при заданной классовой метке. Он вычисляет апостериорную вероятность каждого класса для данного экземпляра и присваивает класс с наибольшей вероятностью.

Основная идея логистической регрессии заключается в том, чтобы прогнозировать вероятность принадлежности наблюдаемого значения к определенному классу. Для этого используется логистическая функция, которая преобразует линейную комбинацию независимых переменных в вероятность.

Алгоритмы DBSCAN и kNN. Как уже упоминалось ранее, алгоритм kNN основан на принципе ближайших соседей, где классификация нового наблюдения (зеленая точка) определяется на основе классов его ближайших соседей в обучающем наборе данных.

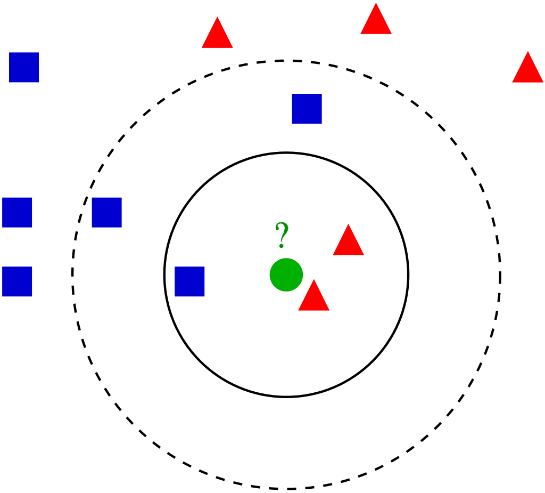
Результат классификации может сильно зависеть от выбора метрики расстояния и числа ближайших соседей. Меньшее число соседей может сделать алгоритм более гибким, но подверженным дисперсии. Выбор метрики расстояний зависит от типа данных и рода задачи, чаще используется Евклидова метрика расстояния. Обучение алгоритма заключается в простом сохранении обучающего набора данных, в сравнении с элементами которого происходит классификация.

DBSCAN – это алгоритм плотностной кластеризации, который группирует экземпляры, близкие друг к другу в пространстве признаков, и отделяет выбросы как шум. Он определяет кластеры как плотные регионы, разделенные более разреженными регионами.

У алгоритма есть два важных параметра: эпсилон (ε) и минимальное количество точек (MinPts). Эпсилон (ε) определяет максимальное расстояние между двумя экземплярами, чтобы они считались соседями. Минимальное количество точек (MinPts) задает минимальное количество экземпляров в пределах расстояния ε для формирования плотного региона.

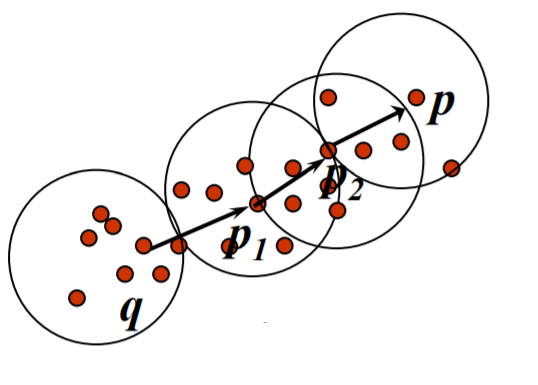
Сформировав один регион, алгоритм исследует регион вокруг следующей случайно выбранной точки и так далее. Если некоторая точка одновременно могла подходить нескольким кластерам, то она присваивается тому кластеру, который дошел до нее раньше. Точки, у которых нет достаточного количества соседей, чтобы считаться критическими, могут войти в плотностный регион, но не могут его образовать. Те точки, что не смогли даже войти в чей-то регион – считаются выбросами.

Оценка качества классификации и кластеризации.

Оценка качества классификации:

• Общая точность: доля правильно классифицированных экземпляров.

• Прецизионность: доля верно положительных экземпляров среди всех экземпляров, предсказанных как положительные.

• Полнота: доля верно положительных экземпляров среди всех фактически положительных экземпляров.

• F1-мера: гармоническое среднее прецизионности и полноты.

TP – наблюдения, которые верно классифицированы как положительные;

TN – коэффициенты, которые верно классифицированы как негативные;

FP – коэффициенты, которые ошибочно отнесены к положительным;

FN – коэффициенты, которые ошибочно отнесены к негативным.

Оценка качества кластеризации:

• Коэффициент силуэта измеряет, насколько хорошо экземпляры сгруппированы, учитывая как сцепление внутри кластеров, так и разделение между кластерами.

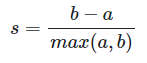
– реднее расстояние между образцом и всеми остальными точками в том же классе;

– среднее расстояние между образцом и всеми другими точками в ближайшем кластере.

• Индекс Дэвиса-Болдуина используется для определения, насколько хорошо объекты внутри каждого кластера сгруппированы (внутрикластерные расстояния) и насколько различны кластеры друг от друга (межкластерные расстояния).

– среднее расстояние между каждой точкой кластера и центроидом этого кластера;

– расстояние между центроидами кластеров и ;

– количество кластеров.

• Индекс Рэнда измеряет сходство между двумя разбиениями данных, учитывая верно положительные, верно отрицательные, ложно положительные и ложно отрицательные экземпляры.

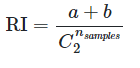
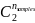– общее количество возможных пар в наборе данных. Не имеет значения, выполняется ли вычисление для упорядоченных пар или неупорядоченных пар, если вычисление выполняется последовательно.

– количество пар элементов, которые находятся в одном наборе в C и в одном наборе в K;

– количество пар элементов, которые находятся в разных наборах в C и в разных наборах в K.

C – набор истинных меток класса, K – набор меток класса после кластеризации.

24. Понятие регрессии. Типы регрессии. Методы численного решения задач регрессии. Способы задания целевой функции в задаче регрессии. Метод наименьших квадратов. Методы машинного обучения для решения задач регрессии.

Понятие регрессии. Цель регрессии – найти наилучшим образом подходящую математическую функцию, описывающую связь между переменными. Зависимая переменная (также называемая откликом или целевой переменной) – это переменная, которую мы хотим предсказать или объяснить, а независимые переменные (также известные как предикторы или признаки) используются для оценки значения зависимой переменной.

Типы регрессии.

Линейная регрессия предполагает линейную зависимость между независимыми и зависимыми переменными. Она направлена на то, чтобы подогнать к точкам данных прямую линию, которая минимизирует сумму квадратов разности между наблюдаемыми и прогнозируемыми значениями.

Полиномиальная регрессия расширяет линейную регрессию, позволяя использовать полиномиальные функции более высокого порядка (например, квадратичные, кубические) для подгонки данных. Это позволяет моделировать более сложные взаимосвязи между переменными.

Множественная регрессия включает в себя более одной независимой переменной. Она позволяет проанализировать, как несколько предикторов в совокупности влияют на зависимую переменную.

Логистическая регрессия используется в тех случаях, когда зависимая переменная является бинарной или категориальной. Она оценивает вероятность наступления события на основе независимых переменных.

Гребневая и Лассо регрессия – методы регуляризации, ассоциированные с регрессией, наиболее часто используются для предотвращения чрезмерной подгонки регрессионных моделей. Они добавляют штрафные члены к объективной функции, поощряя более простые модели.

Методы численного решения задач регрессии.

Некоторые задачи регрессии имеют решения в замкнутой форме, которые могут быть непосредственно вычислены с помощью математических уравнений. Например, простая линейная регрессия может быть решена аналитически методом наименьших квадратов.

Многие задачи регрессии требуют применения методов численной оптимизации для поиска наилучшей функции. В этих методах параметры модели обновляются итеративно до достижения сходимости. Примерами являются градиентный спуск и метод Ньютона.

Способы задания целевой функции в задаче регрессии.

Среднеквадратичная ошибка (MSE) – это наиболее распространенная целевая функция в задачах регрессии. Она измеряет среднеквадратичное отклонение предсказанных значений от фактических значений.

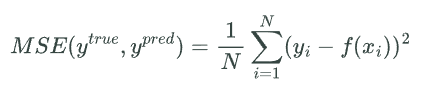
Средняя абсолютная ошибка (MAE) также измеряет среднее отклонение предсказанных значений от фактических значений, но использует абсолютные значения вместо квадратов.

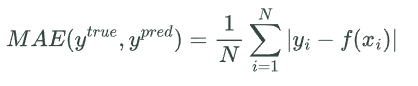
Логарифмическая функция правдоподобия (Log-Likelihood Function) используется в задачах регрессии с методами максимального правдоподобия. Она измеряет вероятность получить наблюдаемые значения зависимой переменной при заданных параметрах распределения в модели.

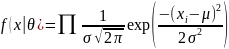
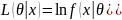
Метод наименьших квадратов. Метод наименьших квадратов является аналитическим подходом к оценке параметров регрессионной модели. Он минимизирует сумму квадратов разности между наблюдаемыми и прогнозируемыми значениями 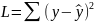. В случае линейной регрессии 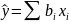, а параметры 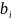, соответствующие минимуму функции 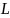, можно найти, приравняв частные производные 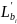к нулю. Хотя, строго говоря, этого недостаточно, и требуется определить знак второй частной производной, чтобы утверждать, что найденные критические точки действительно минимум функции потерь ( ). 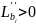Поэтому это аналитическое решение считается довольно вычислительно затратным и часто заменяется итеративными методами поиска оптимальных значений гиперпараметров.

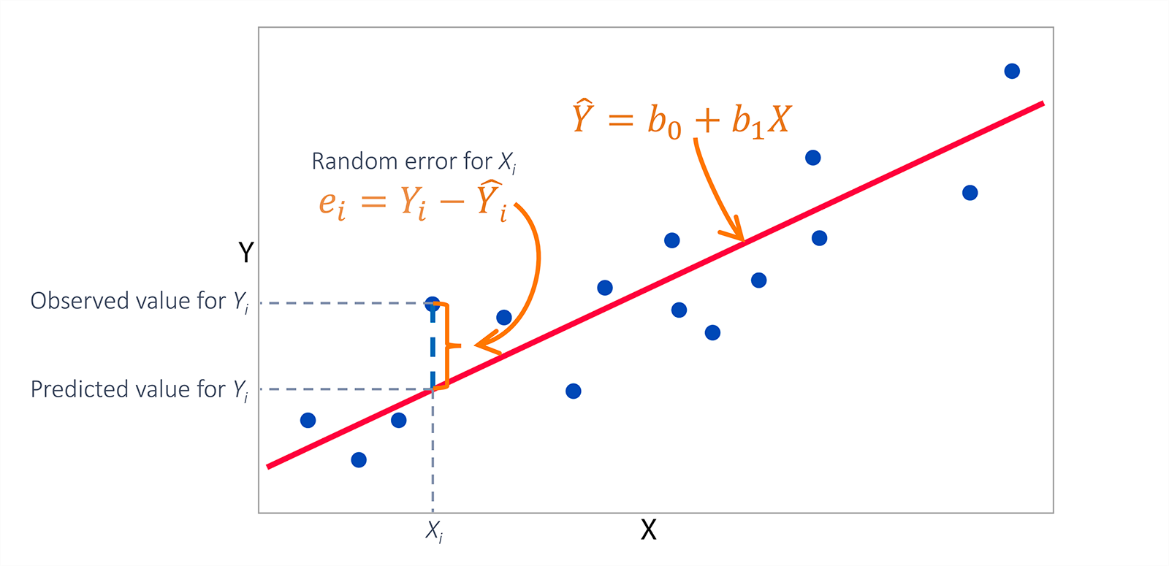
Приведенные выше рассуждения можно переписать в матричном виде:

Методы машинного обучения для решения задач регрессии.

Деревья решений – это универсальные модели машинного обучения, которые могут решать задачи регрессии. Они разделяют пространство признаков на основе пороговых значений и делают прогнозы на основе среднего значения обучающих выборок в каждом узле листа.

Случайный лес – это ансамблевый метод, объединяющий несколько деревьев решений для построения прогнозов. Он позволяет уменьшить перегрузку и получить более точные результаты за счет усреднения прогнозов отдельных деревьев.

Регрессия опорных векторов (SVR) расширяет возможности метода опорных векторов (SVM) для решения задач регрессии. SVR стремится найти гиперплоскость с наибольшим зазором между предсказанными значениями и реальными значениями целевой переменной. Он может использоваться для моделирования сложных нелинейных зависимостей и обладает хорошей способностью к обобщению на новых данных.

Нейронные сети могут быть использованы для решения задач регрессии путем настройки архитектуры сети и функции потерь. Они изучают сложные закономерности и взаимосвязи на основе данных, что делает их пригодными для решения задач нелинейной регрессии.