
- •Линейные пространства векторов. Скалярное произведение. Понятие базиса и линейной независимости элементов линейного пространства. Преобразования базиса.
- •Определение матрицы. Операции с матрицами (умножение на скаляр, сложение, умножение матриц, транспонирование матриц). Обратная матрица и методы ее получения. Функции от матриц.
- •Производные. Необходимое и достаточное условие дифференцируемости функции. Частные производные. Полный дифференциал. Производная и дифференциал сложной функции.
- •Градиент функции. Производные по направлению. Необходимые и достаточные условия экстремума функции многих переменных. Условные экстремумы. Метод множителей Лагранжа.
- •Задачи аппроксимации функций (интерполяция, экстраполяция, приближение в среднем). Способы построения интерполяционного полинома. Аппроксимации на основе ортогональных базисов. Понятие сплайна.
- •Численные методы оптимизации: методы Ньютона и секущей, методы покоординатного и градиентного спуска. Улучшение сходимости градиентных методов.
- •Численные методы оптимизации, основанные на случайных числах. Метод Монте-Карло, линейный случайный поиск, метод оптимизации отжигом.
- •Прямые и итерационные методы решения систем линейных алгебраических уравнений. Методы для систем с матрицами специального вида (ленточные, треугольные, положительно-определенные).
- •Линейные пространства функций (примеры). Скалярное произведение и норма. Операторы над линейными пространствами функций. Функционалы. Собственные числа и функции оператора в пространстве l2.
- •Определение вероятности. Вероятностная модель и вероятностное пространство. Вероятность случайного события и методы ее статистического оценивания по выборке.
- •Модель случайной величины. Закон, функция, плотность распределения. Квантили и моменты распределений, методы их статистического оценивания по выборке.
- •Вероятностные и толерантные интервалы: сходства и различия. Понятия точечного и интервального оценивания. Доверительные интервалы. Несмещенные и эффективные оценки.
- •Параметрическое оценивание распределений случайной величины. Метод моментов. Метод наибольшего правдоподобия и его численная реализация. Способы проверки качества параметрического оценивания.
- •Статистические гипотезы и статистические критерии. Односторонние и двусторонние критерии. Критерии согласия. Параметрические критерии. Ошибки первого и второго рода. Мощность критерия.
- •Модель многомерной случайной величины. Совместные и условные распределения. Условные моменты распределений и их оценивание по выборке. Многомерное распределение Гаусса и его свойства.
- •Случайные процессы и временные ряды. Понятие стационарности. Ковариационная (корреляционная функция). Теорема Карунена-Лоэва. Спектральная плотность случайных процессов.
- •Алгоритмы на графах. Алгоритмы обхода (поиска на) графах. Обнаружение кратчайшего пути и минимального цикла в графе. Построение остовного дерева.
- •Основные понятия машинного обучения. Отличие машинного обучения от статистики. Методы на обучении с учителем. Методы на обучении без учителя. Метрики качества алгоритмов машинного обучения.
- •Цикл обучения. Понятия обучающей и тестовой выборки. Отложенная выборка. Кросс-валидация. Понятия недообучения и переобучения. Дилемма смещения и разброса. Размерность Вапника-Червоненкиса.
- •Понятия классификации и кластеризации. Метрические, иерархические, вероятностные методы классификации и кластеризации. Dbscan и kNn. Оценка качества классификации и кластеризации.
- •Понятие искусственной нейронной сети. Типы нейронных сетей. Понятие стохастического градиента для обучения нейронной сети. Многослойный перцептрон. Сверточные нейронные сети.
- •Методы снижения размерности данных. Метод главных компонент. Метод канонических корреляций. Методы факторного анализа. Нелинейные методы снижения размерности.
- •Принцип повышения размерности пространства. Метод опорных векторов. Понятие и свойства ядра. Метод Kernel-Trick.
- •Построение списка решений и дерева решений. Редукция деревьев решений. Понятие бэггинга и бустинга для деревьев решений. Случайный лес и способы его построения.
- •Обучение с подкреплением. Модели агентов и отклика среды. Задачи, решаемые обучением с подкреплением.
- •Ассоциативный анализ и задача о "покупательской корзине". Алгоритмы аprior и fp-Growth.
- •Способы представления знаний. Модели графов знаний. Полнота графов знаний. Методы прямого и обратного вывода по графам знаний. Онтологическая модель и средства ее реализации.
- •Экспертные методы в принятии решений. Принятие решений при многих критериях. Множество Парето. Экспертные системы поддержки принятия решений.
- •Методы машинного обучения для анализа текстовой информации. Понятие эмбеддинга. Методы построения и использования эмбеддингов при работе с текстом.
- •Генеративные методы машинного обучения. Генеративно-состязательные сети. Вариационные автокодировщики. Байесовские сети. Принципы работы, оценка качества.
Модель многомерной случайной величины. Совместные и условные распределения. Условные моменты распределений и их оценивание по выборке. Многомерное распределение Гаусса и его свойства.
Модель многомерной случайной величины. Во многих реальных сценариях мы сталкиваемся с ситуациями, когда несколько случайных величин взаимосвязаны. Эти переменные можно представить в виде многомерной случайной величины, которая состоит из двух или более случайных величин, где каждая переменная может принимать различные значения одновременно.
Функция плотности вероятности многомерной
случайной величины выполняет следующие
правила:
 для любых возможных реализаций
для любых возможных реализаций
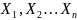 ,
при этом
,
при этом
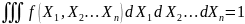 .
.
Кумулятивная функция распределения
многомерной случайной величины выполняет
следующие правила:
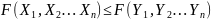 ,
если
,
если
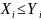 для всех
от 1 до
,
т.е. она нарастает; помимо этого
кумулятивная функция распределения
непрерывна справа, что означает, что
предел
для всех
от 1 до
,
т.е. она нарастает; помимо этого
кумулятивная функция распределения
непрерывна справа, что означает, что
предел
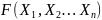 при приближении
при приближении
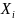 к
к
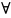 значению справа
значению справа
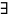 .
.
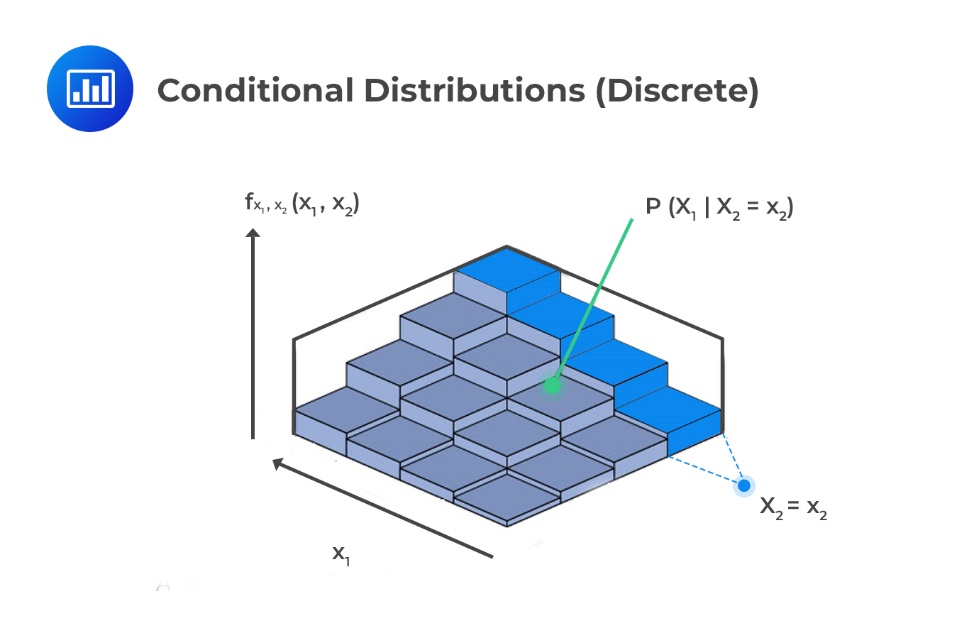
Совместные и условные распределения. Совместное распределение описывает распределение вероятностей всего набора переменных в многомерной случайной величине. В общем-то это обобщенная формулировка для обозначения функции плотности вероятности многомерной величины.
Для дискретной случайной величины
совместное распределение обозначается
как:
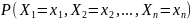 .
.
И, как и в случае с функцией плотности:
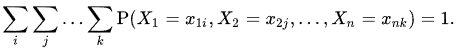
где представляет дискретные случайные величины, а – их соответствующие реализации.
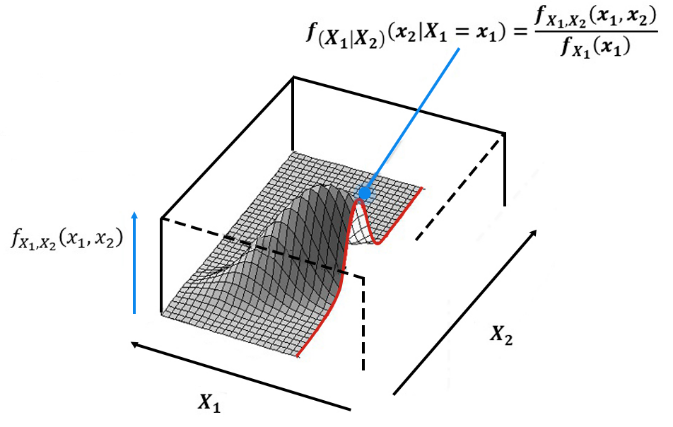
Условное распределение описывает
распределение вероятностей одной или
нескольких переменных, учитывая значения
других переменных. Оно предоставляет
информацию о поведении подмножества
переменных, обусловленном значениями
остальных переменных. В контексте
математической нотации, приведенной
ниже, условное распределение представляет
собой вероятность того, что
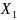 примет значение
примет значение
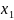 при определенных значениях других
переменных:
при определенных значениях других
переменных:
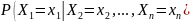
Условные моменты распределений и их
оценивание по выборке. Условные
моменты – это статистические показатели,
которые описывают свойства условного
распределения. Условное среднее,
обозначаемое как
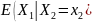 ,
представляет собой среднее значение
при фиксированном значении
,
представляет собой среднее значение
при фиксированном значении
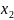 для
для
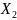 .
Аналогично, условная дисперсия,
обозначаемая как
.
Аналогично, условная дисперсия,
обозначаемая как
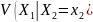 ,
измеряет разброс
вокруг его условного среднего значения,
когда
принимает фиксированное значение
.
,
измеряет разброс
вокруг его условного среднего значения,
когда
принимает фиксированное значение
.
На практике мы часто имеем доступ к
выборке наблюдений, а не ко всей
совокупности. Чтобы оценить условные
моменты по выборке, мы можем вычислить
выборочное среднее:
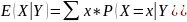 и выборочную дисперсию:
и выборочную дисперсию:
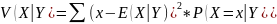 подмножества переменных, обусловленных
конкретными значениями других переменных.
Эти оценки дают приближение к истинным
условным моментам в популяции. Заметим,
что использованные формулы применимы
для дискретных случайных величины, для
непрерывных сумма должна быть заменена
интегралом, а вероятность – функцией
плотности вероятности
подмножества переменных, обусловленных
конкретными значениями других переменных.
Эти оценки дают приближение к истинным
условным моментам в популяции. Заметим,
что использованные формулы применимы
для дискретных случайных величины, для
непрерывных сумма должна быть заменена
интегралом, а вероятность – функцией
плотности вероятности
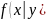 .
.
Многомерное распределение Гаусса и его свойства. Многомерное гауссовское распределение, также известное как многомерное нормальное распределение, является широко используемым распределением вероятностей для моделирования многомерных случайных величин.
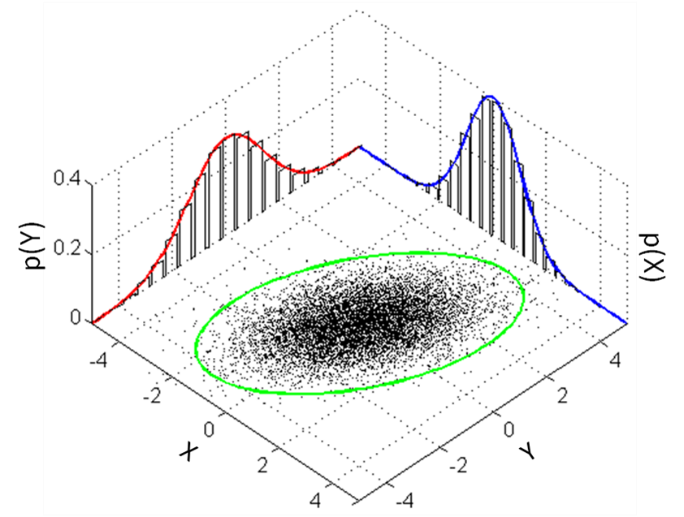
Оно характеризуется средним вектором и ковариационной матрицей. Функция плотности вероятности многомерного гауссовского распределения задается следующей формулой:
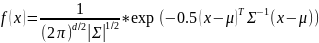
где
– d-мерный вектор случайных величин,
– средний вектор,
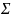 – ковариационная матрица,
– ковариационная матрица,
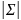 – детерминант
.
– детерминант
.
Многомерное гауссовское распределение обладает несколькими важными свойствами:
Линейные комбинации многомерных гауссовских переменных также являются гауссовскими.
Маргинальные распределения многомерного гауссова распределения являются одномерными гауссовыми.
Условные распределения многомерного гауссовского распределения также являются гауссовскими.
Многомерное гауссовское распределение имеет независимые компоненты тогда и только тогда, когда его ковариационная матрица диагональна.
