Материалы / Тема_3_Реш_функции_норм_Случ_1_сокр

1

Тема 3. Разделяющие функции для случая нормальной плотности

Как мы видели, классификация с минимальным уровнем ошибки может осуществляться посредством разделяющих функций вида

di (x) ln p(x | Ci ) ln P(Ci ) .

Это выражение легко оценивается в случае, когда многомерная плотность p(x | Ci ) нормальна

di (x) 12 (x - mi )T Σi 1 (x - mi ) n2 ln 2 12 ln Σi ln P(Ci ) .

Рассмотрим этот результат в частных случаях.

3.1. Случай 1: Σi 2I .

Простейшая ситуация

- признаки статистически независимы;

-они имеют одинаковую дисперсию 2 .

Ковариационная матрица становится диагональной - произведение 2

на единичную матрицу I.

Геометрия: выборки данных попадают внутрь одинаковых гиперсфер с центром mi (вектор средних значений).

Упрощается расчет

- определителя и матрицы: Σi 2n ,

- обратной i : Σi 1 12 I .

где . евклидова норма, т. е.

x - mi 2 (x - mi )T (x - mi ) .

А. Если все априорные вероятности Р(Ci) равны, то слагаемым ln P(Ci )

можно пренебречь.

Оптимальное решающее правило формулируется очень просто:

чтобы определить класс вектора x , следует измерить евклидово расстояние

x - mi от х до каждого из c векторов средних значений и отнести х к классу,

соответствующему ближайшему среднему значению.

Такой классификатор называют классификатором по минимуму расстояния. Если каждый из векторов средних значений считать эталоном

для образов своего класса, то это по существу будет процедура сравнения с

эталоном.

ln P(Ci ) .

В случае одинаковой близости х к двум различным векторам средних значений следует предпочесть класс, априорно более вероятный.

3

Можно упростить вид решающей функции: раскрытие квадратичной

формы (x - mi )T (x - mi ) приводит к квадратичной функции х:

Квадратичным членом xT x можно пренебречь.

В результате получаем эквивалентную линейную разделяющую функцию вида

di (x) wTi x + wi0 ,

wi 12 mi ,

wi0 21 2 mTi mi ln P(Ci ) .

При условии равенства всех Р(Ci) :

di (x) mTi x 12 mTi mi , i 1, 2,...M . (di (x) max) ,

т.е. образ x относится к классу i, если di (x) d j (x) для всех j i .

Классификатор, основанный на использовании линейных разделяющих функций, называется линейной машиной. Он использует для представления каждого класса в виде одной точки (эталона).

4

Поверхности решений

Поверхности решений в случае линейной машины явятся частями гиперплоскостей, определяемых линейными уравнениями di (x) d j (x) .

Для данного частного случая это уравнение можно записать в виде

гиперплоскость, проходящую через точку х0, т.е. гиперплоскость,

разделяющая Ri и Rj , будет ортогональна прямой, соединяющей их средние значения.

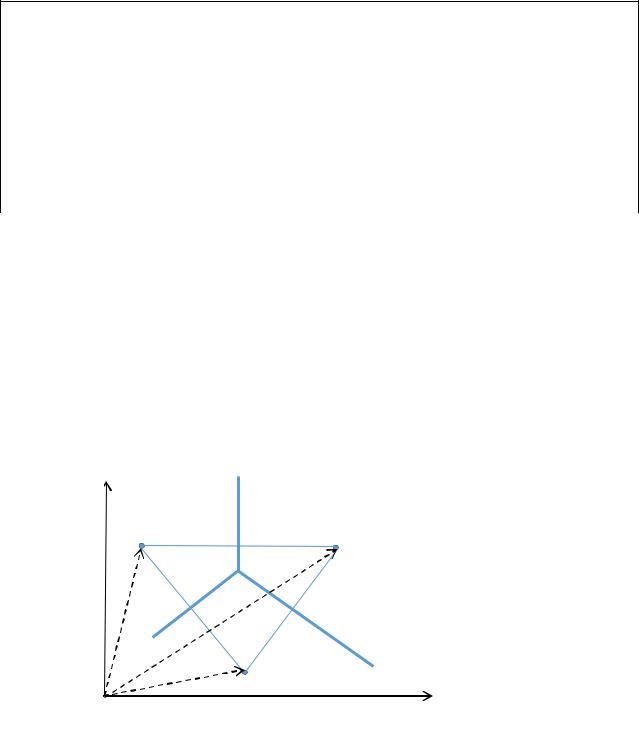
x2

a)

R3

x1

5

Такое представление справедливо для случая нормального распределения с

равными дисперсиями по каждой координате.

X

w

(m1-m2)

b)

Рис.1. Границы областей решений при использовании классификатора по минимуму

расстояния: a)трѐхклассовая задача; b) двухклассовая задача.

2.Если P(Ci ) P(Cj ) , то точка х0 находится посередине, а

гиперплоскость проходит через середину отрезка, соединяющего средние значения перпендикулярно ему (рис. 1).

зависит от значений априорных вероятностей.

6

Построение решающего правила

(классификатором по минимуму расстояния)

Решающее правило (P(C1 ) P(C 2 )) будет иметь следующий вид.

Разделяющая функция

wT (x x0 ) 0 или (wT x wT x0 ) ,

и вектор

x0 12 (m1 + m2 ).

Или

d(x) d1(x) d2 (x) wT x - a 0 ,

a wT x0 xT0 w 12 (m1 + m2 )T w.

Тогда дискриминантную функцию можно привести к стандартному виду

D(X) WтX a 0,

где W – весовой вектор единичной длины; a – пороговая величина. Для этого разделим все члены выражения на m1 m2 , . - норма (длина вектора).

В этом случае (так как WтX X сosα ) процедура распознавания заключается в вычислении проекции вектора X на направление весового вектора W и

сравнении полученной величины с порогом a.

7

α

W

a

|X| сos α

Рис.2. К определению D(X)

Ясно, что разделяющая гиперплоскость проходит перпендикулярно к W на расстоянии a от начала координат.

Тогда весовой вектор

И решающее правило принимает вид

WT X < a , то класс R1 ;

WT X > a , то класс R2 .

Алгоритм распознавания (2 класса)

1.Вычислить весовой вектор w (w1, w2 ,..., wn ) .

2.Пронормировать этот вектор ( ww ), сделав его единичным вектором

W.

3.Спроектировать точки обоих классов на прямую линию, определяемую положением W, и построить их одномерные гистограммы.

4.Найти точку на этой прямой (порог a).

5.Определить разделяющую гиперплоскость WT X a 0 и соответствующий алгоритм распознавания.

8

Для трѐхклассовой задачи возможны несколько вариантов решений.

2.Используя метод главных компонент, найти наиболее удаленный

(или более плотно сгруппированный) класс, отделив его от двух остальных (1 этап). Затем решить задачу классификации двух оставшихся классов (2 этап).

3.Строить решающие функции для каждой пары соседних классов.