Структуры данных в языке lisp
LISP отличается от прочих языков программирования следующими свойствами [McCarthy et al, I960]:
основной структурой данных в нем является список;
программы на этом языке также имеют списочную структуру;
его базовыми операциями являются операции над списками.
Базовым блоком в структуре данных языка LISP является символическое выражение.
Списки представляют собой довольно гибкие структуры данных, поскольку могут объединять элементы разных типов и иметь произвольную длину и размерность (вложенность). Но списки имеют и определенные недостатки, из-за которых в LISP были включены и другие структуры данных. Списки в LISP представляют собой стеки, т.е. доступ к ним возможен только с одного конца списка. Манипулируя только таким списком, невозможно обратиться к элементу списка по его позиции, как это делается с элементом массива. Поэтому для представления больших совокупностей относительно постоянных или редко меняющихся данных в LISP были включены другие типы структур. В современных версиях LISP поддерживаются массивы, хэш-таблицы и структуры, подобный записям, которые позволяют эффективнее использовать пространство памяти и повысить скорость доступа.
Обработка списков
Большинство LISP-программ можно специфицировать, используя только пять простейших операторов над символическими выражениями и одну специальную форму (условное выражение).
Как оказалось, структурой, наиболее подходящей для нечисловых вычислений, являются списки. Именно такие вычисления необходимо выполнять в процессе поиска решения в пространстве альтернатив. В списке можно держать в поле зрения те альтернативные варианты, которые уже были рассмотрены ранее, не которые еще предстоит рассмотреть, и т.д. Поскольку между списками и древовидными ориентированными графами существует изоморфизм, естественно представлять развернутое пространство состояний в виде одного или более списков.
Сопоставление с образцом
Одним из ключевых компонентов в большинстве программ искусственного интеллекта является анализатор соответствия (pattern matcher) — компонент, который некоторым образом сравнивает поступающие на его вход списки (или другие структуры данных) с имеющимися символическими образцами и таким образом выполняет распознавание входных данных.
Анализ соответствия — это довольно "расточительная" операция в смысле расхода вычислительных ресурсов, если только не пользоваться ею с умом. В настоящее время язык LISP не используется для реализации систем, базирующихся на правилах, в основном из-за недостаточной его эффективности, но по-прежнему используется тот принцип обработки списков при анализе соответствия, который был впервые реализован на LISP.
Определение функции принадлежности. Виды и примеры функций принадлежности. Примеры.
Определение функции принадлежности
Для
пространства рассуждения
X {\displaystyle
\mathbf {X} \ } и
данной функции принадлежности
{\displaystyle
\mu :\mathbf {X} \to [0,1]} нечёткое
множество определяется как
{\displaystyle
{\tilde {\mathit {A}}}=\{(x,\mu _{A}(x))\mid x\in \mathbf {X} \}.}
Функция
принадлежности {\displaystyle
\mu _{A}(x)\ }
количественно
градуирует принадлежность элементов
фундаментального множества пространства
рассуждения 
{\displaystyle
x\in \mathbf {X} }
нечёткому
множеству {\displaystyle
{\tilde {\mathit {A}}}}
.
Значение {\displaystyle
0\ }0 означает,
что элемент не включен в нечёткое
множество, {\displaystyle
1\ }1 описывает
полностью включенный элемент. Значения
между {\displaystyle
0\ }0 и {\displaystyle
1\ }1 характеризуют
нечётко включенные элементы.
Виды и примеры функций принадлежности.
Кусочно-линейные функции принадлежности. Одним из наиболее простых типов функций принадлежности являются функции, которые, как следует из их названия, состоят из отрезков прямых линий. Типичными примерами таких функций являются "треугольная" (рис. 1.8) и "Трапециевидная" (рис. 1.9) функции принадлежности.
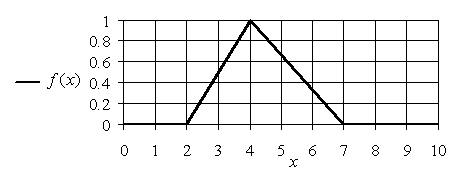
Треугольная функция принадлежности в общем случае может быть аналитически задана следующим выражением:
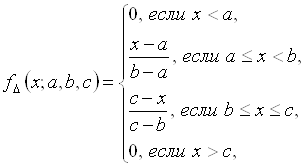
Где
a,b,c
– некоторые числовые параметры,
принимающие произвольные действительные
значения и упорядоченные отношением:
Для конкретной функции, изображенной на рис., значения параметров следующие: a=2, b=4, c=7. Эта функция принадлежности порождает нормальное выпуклое унимодальное нечеткое множество с носителем – интервалом, (a,c) , границами, (a,c)\{b} , ядром {b} и модой b .
Трапециевидная функция
Трапециевидная функция принадлежности в общем случае может быть аналитически задана следующим выражением:
Где
a,b,c,d–
некоторые числовые параметры, принимающие
произвольные действительные значения
и упорядоченные отношением:
.
Z-образные и S -образные функции принадлежности. Эти функции принадлежности также получили свое название по виду кривых, которые представляют их графики.
Z-Образная функция принадлежности может быть задана аналитически, например, следующим выражением:
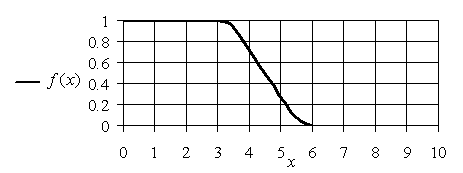
Где a,b – некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: a < b.
S-образная функция принадлежности может быть задана аналитически следующим выражением:
Где a,b – некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: a<b.
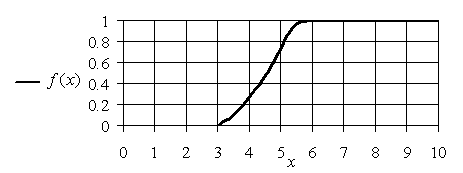
График этой функции для некоторого нечеткого множества A и универсума X = [0,10] изображен на рис.
Линейная S-Образная функция в общем случае может быть задана аналитически следующим выражением:
Где a,b – некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: a<b.
График этой функции для некоторого нечеткого множества A и универсума X = [0,10] изображен на рис.
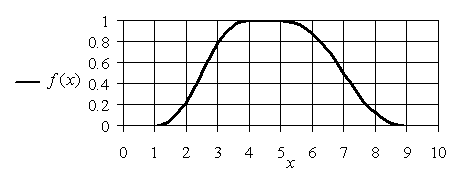
П-образные функции принадлежности. К этому типу функций принадлежности можно отнести целый класс так называемых колоколообразных кривых.
Один из возможных способов задания П -образной функции принадлежности состоит в использовании композиции S -Образной и Z -Образной функций в соответствии с соотношением:
Где
a,b,c,d
– некоторые числовые параметры,
принимающие произвольные действительные
значения и упорядоченные отношением
.
3В