4.1. Признаки в пространственной области 4.1.2. Структурные (вероятностные) признаки изображений

Нормализованная взаимная корреляция

Приведение шаблона и изображения к однородной шкале: вычитание среднего и деление на среднеквадратическое отклонение.

4.1.Признаки в пространственной области

4.1.2.Структурные (вероятностные) признаки изображений

Проблемы при сопоставлении изображения с шаблоном

OCR – optical character recornition

4.1.Признаки в пространственной области

4.1.2.Структурные (вероятностные) признаки изображений

Признаки стохастической геометрии

Признаки стохастической геометрии описываются случайными величинами,

связанными с наступлением каких-либо геометрических событий.

Чаще всего для получения этих признаков на плоскости изображения генерируется линия, положение которой задается случайным образом, и вычисляются некоторые характеристики, связанные с пересечением этой линией выбранного объекта на изображении. Напр., это может быть число пересечений объекта линией; максимальная или минимальная длина отрезка линии, попавшего на объект; суммарная длина отрезков линии, находящихся в области объекта, и т.д. Вероятностные характеристики таких

случайных величин некоторым образом описывают форму объекта.

В силу случайности положения линии, эти признаки инвариантны к смещениям и поворотам изображения; к масштабу (при определенных условиях).

Достоинством таких признаков является относительно высокая помехоустойчивость.

4.1. Признаки в пространственной области 4.1.2. Структурные (вероятностные) признаки изображений

Признаки стохастической геометрии Гистограмма ориентации

контурных элементов изображения –

распределение количества контурных элементов по длине вектора ρ и направлению φ.

Для построения гистограммы ρ-φ следует:

1.Подсчитать количество контурных элементов в различных диапазонах длин, независимо от их ориентации, и построить гистограмму. 2.Подсчитать количество контурных элементов, ориентированных в заданных диапазонах углов, независимо от размеров, и построить гистограмму.

3.Построить двумерную гистограмму частот по параметрам ρ и φ.

4.1.Признаки в пространственной области

4.1.2.Структурные (вероятностные) признаки изображений

Признаки стохастической геометрии

Сложность при измерении длины контурных элементов на изображении заключается в том, что они редко представляют собой прямые линии.

Обычно это искривленные линии с множеством плавных и резких перегибов, кроме того, весьма вероятно пересечение и размножение этих кривых.

Контурный элемент может быть представлен в виде отрезка прямой, произвольно ориентированной в плоскости изображения: в этом случае после выбора точки отсчета (начала отрезка) измерение осуществляется согласно евклидовой метрике.

Контурный элемент может представлять собой кривую, тогда она разбивается на ряд линейных участков, при этом точность измерений определяется минимальным размером аппроксимирующего элемента.

Если в контуре имеются разветвления, применяют следующие приемы: учитывают только максимальную длину; учитывают только особые кончики (напр., с завихрениями); учитывают сумму всех частей; не учитывают ответвления.

При подсчете количества контурных элементов (с учетом их ориентации) для криволинейных участков контура вычисляются все углы промежуточных звеньев, на которые они разбиты (точность растет при уменьшении длины

отрезка). Общую ориентацию замкнутого контура определяют, исходя из ориентации всех составляющих его отрезков.

4.1.Признаки в пространственной области

4.1.2.Структурные (вероятностные) признаки изображений

Признаки стохастической геометрии

Анализ осколков настенного рисунка для создания алгоритмов реставрации

Типы

разветвлений

4.2. Признаки в частотной области. Спектральные признаки

Спектральные признаки – это признаки, в процессе получения которых используется спектральная модель преобразования изображения:

N −1M −1

FW (u,v) = ∑ ∑B(x, y)W (x, y,u,v)

x=0 x=0

B(x, y) – яркость точки на изображении с координатами (x, y); W(x, y, u, z) – ядро преобразования.

Спектральные коэффициенты, найденные в результате двумерного преобразования, определяют веса двумерных базисных функций (базисных изображений), соответствующих этому преобразованию, при которых взвешенная сумма базисных функций идентична изображению.

Эти коэффициенты показывают степень корреляции соответствующих базисных функций с изображением. Поэтому если базисное изображение имеет ту же пространственную форму, что и признак, который требуется обнаружить на изображении, то для его обнаружения достаточно определить соответствующий спектральный коэффициент.

Для получения спектральных признаков применяют Фурье-преобразование, косинусное преобразование, преобразование Радона, вейвлет-преобразование и др.

4.2. Признаки в частотной области. Спектральные признаки

Фурье-преобразование изображения в непрерывной области имеет вид

F(u,v) = ∞∫ ∞∫B(x, y)e − j2π(xu+yv)dx dy

−∞−∞

В дискретной области применяют быстрое преобразование Фурье (БПФ)

u и v – горизонтальная и вертикальная пространственные частоты; N × M – размеры исходного изображения (в пикселях);

B(x, y) – яркость точки на изображении с координатами (x, y); j – мнимая единица.

Преобразование Фурье задает комплексное число для каждой точки частотной плоскости (u, v).

C помощью обратного БПФ функция F(u, v) может быть трансформирована в

u=0 v=0

4.2. Признаки в частотной области. Спектральные признаки

БПФ-изображение м.б. отображено с использованием 4х комплексных компонентов: действительная часть и мнимая часть, амплитуда и фаза.

Соотношение между этими компонентами:

F(u,v) = Re(u,v) + j Im(u,v)

Re(u, v) – действительная часть и Im(u, v) i – мнимая часть.

F(u,v) = F(u,v) e jϕ(u,v)

|F(u, v)| – амплитуда и φ(u, v) – фаза.

Амплитуда |F(u, v)| также называется спектром Фурье:

F(u,v) = 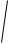Re(u,v)2 + Im(u,v)2

Фаза также называется фазовым углом:

ϕ(u,v) = arctg Im(u,v)Re(u,v)

4.2. Признаки в частотной области. Спектральные признаки

Возможно 2 представления БПФ-изображения (спектра БПФ):

стандартное и оптическое. Значения яркости точек на БПФ-изображении пропорциональны амплитудам спектра БПФ в соответствующих точках.

4.2. Признаки в частотной области. Спектральные признаки

В оптическом (центрированном) представлении низкие частоты группируются в центре изображения, а высокие располагаются по краям.

Постоянная составляющая или нулевая частота находится в центре изображения.

Шкала пространственных частот: [-N∆u/2, N∆u/2] × [-M∆v/2, M∆v/2].

4.2. Признаки в частотной области. Спектральные признаки

БПФ спектры изображений с видимой периодической структурой и без нее