2.2. Условия выполнения закона Бугера-Ламберта-Бера.

Как и все физические законы, закон Бугера-Ламберта-Бера выполняется при соблюдении во время измерений определенных условий. Рассмотрим эти условия.

Данный закон будет соблюдаться, если:

1. тестирующее излучение монохроматично, т.е. все его кванты имеют одинаковую энергию (длину волны, частоту и волновое число);

2. пучок тестирующего излучения параллелен и падает строго нормально на переднюю границу образца;

3. сам объект имеет плоскопараллельную форму, т.е. его передняя и задняя (по отношению к источнику излучения) границы представляют собой параллельные друг другу плоскости, и толщина объекта во всех его точках одинакова;

4. интенсивность тестирующего излучения и среднее время пребывания молекул-хромофоров в состоянии возбуждения после поглощения кванта, таковы, что примесью образующихся в образце молекул в возбужденном состоянии можно было пренебречь;

5. хромофорные молекулы распределены по объёму объекта равномерно, т.е. концентрация хромофора во всех точках объекта одинакова;

6. в образце за время измерения не наблюдаются значимые изменения его состава вследствие протекания фотохимических реакций;

7. все хромофорные молекулы пребывают в одном и том же агрегатном состоянии;

8. истинное поглощение есть единственная причина снижения числа квантов излучения, попадающих на фотодетектор измеряющего прибора.

Как видно из представленного, требования к тестирующему излучению и свойствам объекта, выполнение которых необходимо для того, чтобы закон Бугера-Ламберта-Бера соблюдался, довольно строги. Рассмотрим теперь, к чему приведет их несоблюдение.

Если тестирующее излучение немонохроматично, т.е. состоит из квантов с разными энергиями (длинами волн, частотами и волновыми числами), то, поскольку величина молярного коэффициента поглощения () для каждого типа квантов будет иметь собственное значение, при последующем расчёте концентрации хромофора в объекте по формуле D = cl будет сделана ошибка (в ней используется величина  для вполне конкретной длине волны). Если же анализируется концентрационная зависимость D, то она в таких условиях может сильно отклоняться от линейной.

Если пучок тестирующего излучения, падающий на объект, не параллелен (т.е. является сходящимся или расходящимся), то те кванты света, которые попадут в объект не по нормали, будут иметь другой оптический путь, чем кванты в середине пучка (рис. 3). Из-за этого величина D также окажется измеренной неверно, а концентрация хромофора определена с ошибкой.

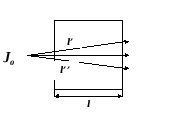
Рисунок 3. Схема, иллюстрирующая влияние непараллельности тестирующего пучка излучения на результаты измерения оптической плотности. Если пучок тестирующего излучения J₀, как в приведенном примере, расходящийся, то для квантов, близких к его середине оптический путь будет равен толщине образца (l), тогда как кванты, попадающие в объект ненормально, будут иметь оптические пути l’ и l’’, которые значительно отличаются от l. Аналогичная ситуация будет наблюдаться и в случае, если пучок тестирующего излучения будет сходящимся.

Если объект не имеет плоскопараллельной формы (например, измерения проводятся в круглой кювете), его толщина в разных точках будет неодинакова. Следовательно, кванты тестирующего излучения пройдут разные оптические пути, и измеренная величина D будет ошибочна.

Если интенсивность J₀ тестирующего излучения избыточно высока, а исследуемые молекулы долго пребывают в возбужденном состоянии после поглощения кванта (например, формируются триплетные возбуждения, см. выше), будет наблюдаться следующее. Во-первых, возбужденные молекулы являются новым типом хромофора с собственной величиной . Во-вторых, за счет формирования долгоживущих возбужденных молекул может заметно упасть концентрация невозбужденных. Наконец, в-третьих, длительно живущие возбужденные молекулы могут успеть поглотить второй квант излучения и перейти в еще более возбужденное состояние. Все указанные процессы приводят к тому, что зависимость D от концентрации хромофора перестает быть линейной, т.е. закон Бугера-Ламберта-Бера перестает соблюдаться.

Если хромофорные молекулы распределены по объему образца неоднородно и концентрация хромофора в разных частях объекта неодинакова, измеряемая оптическая плотность объекта будет занижена.

Попробуем доказать это математически.

Сопоставим однородный и неоднородный объекты при условии, что количество хромофора в обоих случаях одинаково. Для этого введем следующие обозначения:

• S - площадь освещенной поверхности объектов, совпадающая с площадью тестирующего пучка монохроматического излучения;

• J₀ – световой поток, падающий на эту поверхность, выраженный в квантах/секунду;

• m – количество хромофора в объектах, выраженное в молях;

• dm/dS – поверхностная плотность хромафора

В случае однородного объекта

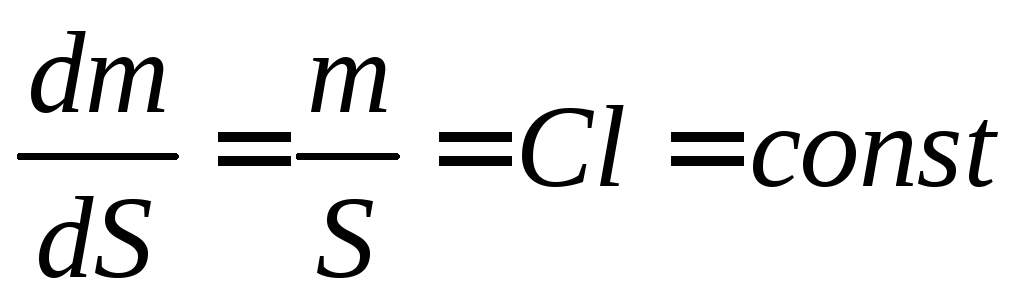
где С и l – концентрация вещества в объекте (количество вещества в единице объема) и толщина объекта. Согласно закону Бугера-Ламберта-Бера:

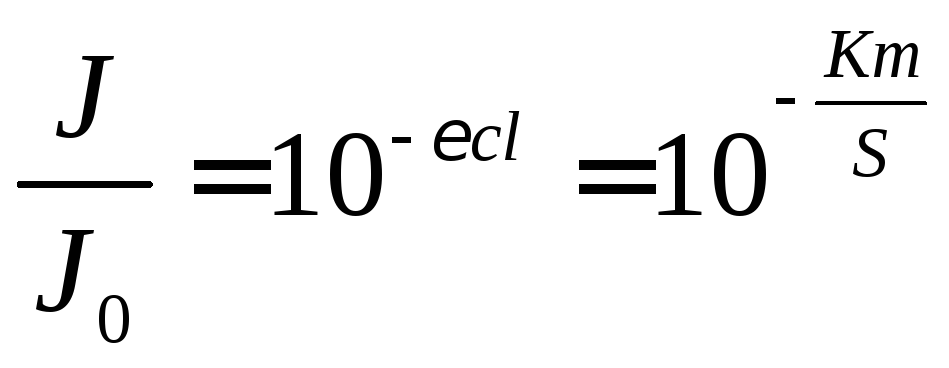
где К – поверхностный коэффициент поглощения, равный 10^-3 моль^-1см²; а J – выходящий из объекта световой поток.

Для неоднородного объекта

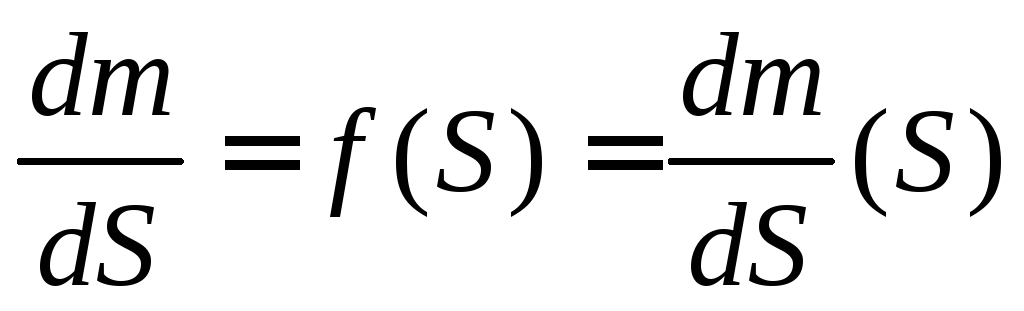
При этом вид зависимости dm/dS=f(S) неизвестен.

Разобъем неоднородный объект на такие маленькие фрагменты площадью dS каждый, чтобы неоднородностью распределения хромофора в пределах фрагмента можно было пренебречь. Закон Бугера-Ламберта-Бера в каждом из фрагментов будет выполняться и, соответственно, выходящий из каждого фрагмента световой поток dJ будет равен:

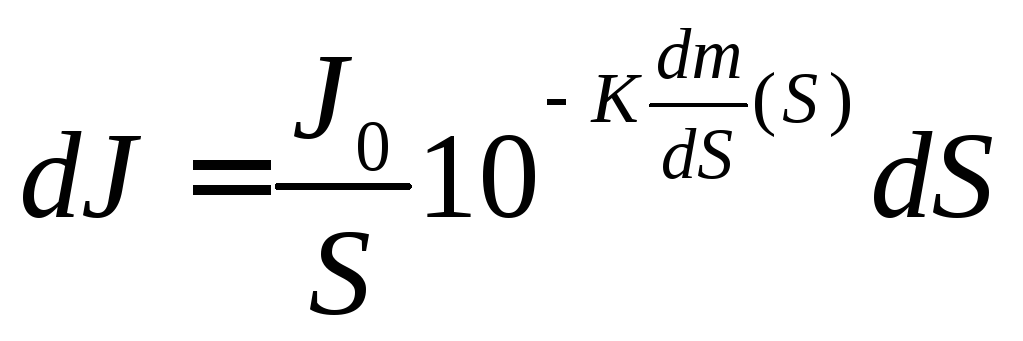
Полный световой поток J’, выходящий из неоднородного объекта площадью S, тогда будет составлять:

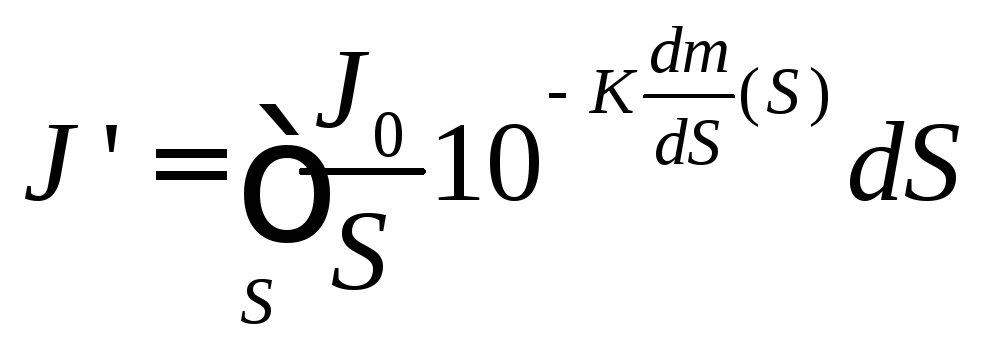
Отсюда

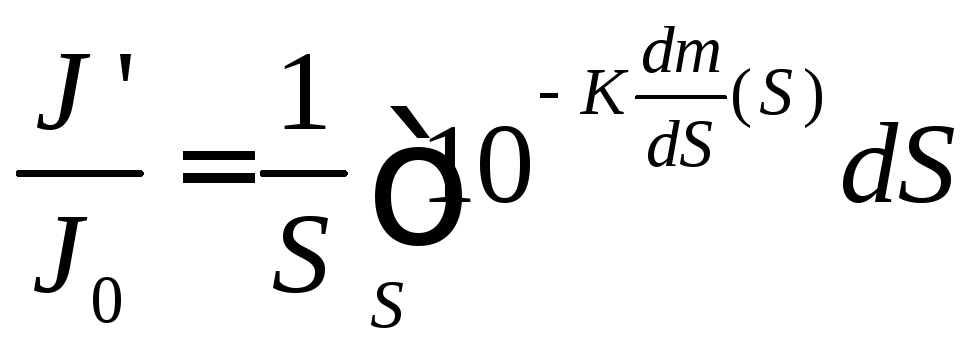
Трансформируем последнее уравнение в следующий вид:

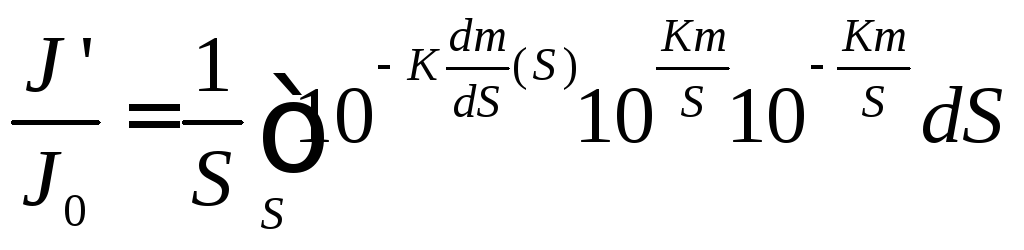
Разложим подинтегральное выражение в ряд Тейлора и будет интегрировать его по частям:

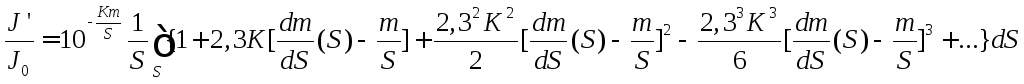
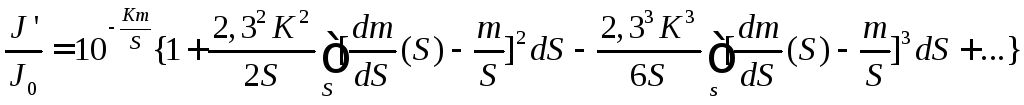
Прологарифмировав последнее уравнение с учетом того, что lg(J₀/J’)=D’ (оптическая плотность неоднородного объекта), а Km/S = D (оптическая плотность однородного объекта), получим:

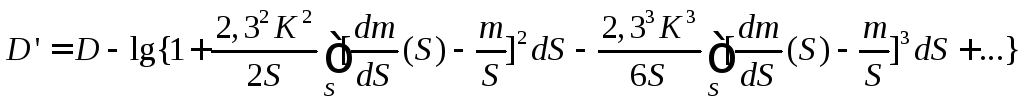
Тот факт, что D’ меньше D можно будет считать доказанным, если различающий эти величины логарифм положителен. Логарифм будет положителен, если логарифмируемая величина больше 1. В нашем случае это так, поскольку к 1 под знаком логарифма добавлен квадратичный член разложения в ряд Тейлора, который всегда положителен. Остальные же члены этого ряда будут значительно меньше, и на результат не повлияют. Таким образом, оптическая плотность объекта с неоднородным распределением хромофора всегда меньше, чем оптическая плотность однородного объекта с тем же общим количеством хромофора.

Впрочем, понять, почему D’ меньше D можно и не прибегая к математическим выкладкам, на основании простых логических рассуждений. Действительно, предельный случай неоднородного распределения хромофора в объекте – это случай, когда все хромофорные молекулы сосредоточены в пределах безразмерной точки. Поток света через эту точку будет равен 0, поскольку у неё нулевая площадь поперечного сечения. Таким образом, и оптическая плотность такого, предельно неоднородного, объекта будет равна 0. Все остальные случаи неоднородного распределения хромофора по объекту являются промежуточными между этим, предельным, случаем, и идеально однородным раствором хромофора. Следовательно, и оптическая плотность промежуточных по неоднородности объектов должна быть больше 0, но меньше оптической плотности образца с идеально однородным раствором.

Частным случаем влияния неоднородности распределения хромофора в объекте на его оптическую плотность является так называемый эффект сита. Поскольку этот эффект весьма часто наблюдается в клеточных суспензиях, типичном биологическом объекте, мы рассмотрим его более подробно ниже.

Если во время измерения под влиянием тестирующего излучения в образце во время измерения оптической плотности протекают значимые фотохимические реакции, количество исходных молекул-хромофоров может значительно уменьшится. Вместе с тем, в образце будут появляться продукты фотохимической реакции, которые являются другим типом молекул с новой структурой электронных энергетических уровней (орбиталей). Если молекулы-продукты будут способны к поглощению квантов излучения при той длине волны, при которой проводится измерение, часть измеряемой оптической плотности окажется связана с их присутствием. Однако величина молярного коэффициента поглощения () у молекул-продуктов при длине волны измерения будет иной, чем у исходных молекул, из-за чего расчеты концентрации исходного соединения по формуле D = cl дадут неверный результат.

Если хромофорные молекулы в объекте представлены в нескольких агрегатных формах, например, в виде мономера и димера, то каждая из этих форм будет иметь при длине волны тестирующего излучения собственную величину  (обозначим их _м и _д соответственно). В результате измеренное значение оптической плотности (D_изм) будет равно:

Соотношение же концентраций мономерной и димерной форм хромофора (с_м и с_д) зависит от количества вещества в образце и его растворимости в применяемом растворителе в данных условиях. Чаще всего, это соотношение неизвестно. Нередко неизвестен и _д (молярный коэффициент поглощения димерной формы хромофора). Естественно, в таких условиях применение закона Бугера-Ламберта-Бера невозможно, и определение концентрации соединения по величине D_изм даст неверный результат.

Молекулярные агрегаты (ди-, три- , тетрамеры и агрегаты большей величины) обычно начинают формироваться, если концентрация вещества в объекте близка к пределу его растворимости в используемом растворителе. Чтобы избежать их образования, при спектрофотометрии не следует применять растворители, в которых определяемое соединение растворяется плохо, и не следует подвергать исследованию растворы хромофоров очень высокой концентрации.

Если истинное поглощение излучения – не единственная причина снижения количества квантов, попадающих на фотодетектор фотометра (прибора для измерения поглощения света), измеряемая величина оптической плотности окажется завышенной. Соответственно, завышена окажется и рассчитанная величина концентрации хромофора в объекте.

Наиболее частой причиной такого эффекта является наличие в образце рассеивания света. Поскольку это явление чрезвычайно часто встречается в биологических объектах, ему будет посвящен специальный раздел ниже.