
- •Лабораторнаяработа
- •Изучение основных свойствэлектростатическогополя методическиеуказания
- •Лабораторнаяработа№ 2э.2 изучение основных свойств электростатического поляцельработы
- •Методическоеобоснование
- •Потенциал
- •Описаниеэкспериментальнойустановки
- •Подготовка лабораторной установки к работеиметодикаизмерений
- •Обработкарезультатовизмерений
- •Задание
- •Контрольныевопросы
- •Рекомендованнаялитература
 МинистерствообразованияРеспубликиБеларусьБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
МинистерствообразованияРеспубликиБеларусьБЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедрафизики
Лабораторнаяработа
№2э.2
Изучение основных свойствэлектростатическогополя методическиеуказания
Минск2023
Лабораторнаяработа№ 2э.2 изучение основных свойств электростатического поляцельработы
 Изучитьхарактеристикивекторногополя:потокΦЕчерезориентиро-ваннуюповерхностьициркуляцию
ΓЕвдольориентированногоконтура.
Изучитьхарактеристикивекторногополя:потокΦЕчерезориентиро-ваннуюповерхностьициркуляцию
ΓЕвдольориентированногоконтура.ПроверитьтеоремуГауссадляполявекторанапряженностиEэлек-трического полявинтегральной форме.
Проверитьравенствонулюциркуляциивекторанапряженности E
электростатическогополявдольпроизвольногоориентированногоконтура.
Методическоеобоснование
Всякий заряд (частица или тело, обладающее зарядом) изменяет опреде-ленным образом свойства окружающего его пространства – создаетэлектриче-ское поле, которое проявляет себя в том, что помещенный в какую-либо еготочкудругойзарядиспытываетдействиесилы со стороныэтогополя.
Основной характеристикой электрического поля является напряженность.НапряженностьEэлектрического поля в некоторой его точке – векторнаяфизическаявеличина,являющаясясиловойхарактеристикойэлектрическогопо-ляиравнаяотношениюсилы⃗,действующейсостороныполянапомещенныйв
 даннуюточкунеподвижныйточечныйпробныйзарядqпр,кэтомузаряду:
даннуюточкунеподвижныйточечныйпробныйзарядqпр,кэтомузаряду:
-
E(r)F(r).
qпр
(1)
В СИ[Е]= В/м.
![]() Электростатическим
полемназывается электрическое поле,
создавае-мое
неподвижными в выбранной системе отсчета
зарядами. Кроме
напряжен-ностиважнойхарактеристикойэлектростатическогополяявляетсяпотенциал.
Электростатическим
полемназывается электрическое поле,
создавае-мое
неподвижными в выбранной системе отсчета
зарядами. Кроме
напряжен-ностиважнойхарактеристикойэлектростатическогополяявляетсяпотенциал.
Потенциал
(r)
точкиэлектростатическогополя–скалярнаяфизиче-
![]() скаявеличина,являющаясяэнергетическойхарактеристикойэтогополявдан-
скаявеличина,являющаясяэнергетическойхарактеристикойэтогополявдан-
нойточкеиравнаяотношениюпотенциальнойэнергии
Wp(r),
которойобла-
 даетнаходящийсявданнойточкепробныйточечныйзарядqпр,кэтомузаряду:
даетнаходящийсявданнойточкепробныйточечныйзарядqпр,кэтомузаряду:
-
Wp(r)(r) .
qпр
(2)
В СИ[φ]=В.
![]()
 Связьнапряженностиэлектростатическогополяипотенциала:векторнапряженности
в данной точке с радиус-векторомrэлектростатического
поляравенградиентупотенциалавэтойточкеполясобратнымзнаком:
Связьнапряженностиэлектростатическогополяипотенциала:векторнапряженности
в данной точке с радиус-векторомrэлектростатического
поляравенградиентупотенциалавэтойточкеполясобратнымзнаком:
-
Ergrad(r).
(3)
В декартовой прямоугольной системе координат (ДПСК) равенство (3)принимаетвид:

EreEreEre(r)e(r)e(r)e, x x y y z z x x y y z z |
(4) |
где
Exr,
Eyr,
Ez
–проекциинапряженностиEвточкеэлектростати-
![]()
![]()
 ческогополясрадиус-векторомrнакоординатныеосиДПСК;
ческогополясрадиус-векторомrнакоординатныеосиДПСК;
![]() ex,
ex,
ey,ez
–ортонормированныйбазисДПСК.
![]()
![]() Стационарным
векторным полем(например, полем
вектора напряжен-ностиEэлектростатического
поля) называется область пространства,
в
каждойточкекоторойзаданнезависящийотвременивекторE,т.е.определенавек-
Стационарным
векторным полем(например, полем
вектора напряжен-ностиEэлектростатического
поля) называется область пространства,
в
каждойточкекоторойзаданнезависящийотвременивекторE,т.е.определенавек-

 торнаяфункциякоординатEEr,гдеr –радиус-векторточкиобластипространства.
торнаяфункциякоординатEEr,гдеr –радиус-векторточкиобластипространства.
Силоваялиниявекторногополя
EE(r)
−этонаправленнаялиния,в
каждой точке которой векторEнаправлен по касательной к силовой линии.Густота силовых линий (т. е. число силовых линий, пересекающих перпендику-лярную к ним плоскую поверхность единичной площади) в некоторой точкеполяпрямо пропорциональнамодулюЕвектораEвэтой точке.
Интегральнымихарактеристикамивекторногополя,описывающимиос-
новныеегосвойства,являются:
потокΦЕчерезориентированнуюповерхность,
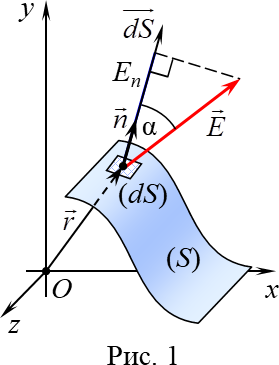 циркуляция
ΓЕвдоль
ориентированного
контура.Пустьвокрестностикакой-либоточкивектор-
циркуляция
ΓЕвдоль
ориентированного
контура.Пустьвокрестностикакой-либоточкивектор-
ногополя
EE(r)
находитсямалыйплоскийэлемент
![]()
 (dS)
некоторой поверхности (S), в пределах
которогоданноеполеможносчитатьоднородным,т.е.векторEв
каждой точке элемента (dS)
одинаков (рис. 1).Ориентируем
этот элемент (dS) заданием
единичноговекторанормалиn(n1),проведенногоперпенди-
(dS)
некоторой поверхности (S), в пределах
которогоданноеполеможносчитатьоднородным,т.е.векторEв
каждой точке элемента (dS)
одинаков (рис. 1).Ориентируем
этот элемент (dS) заданием
единичноговекторанормалиn(n1),проведенногоперпенди-
 кулярнок(dS).Посколькумалыйэлемент(dS)по-верхности
является плоским, то вектор нормалиnк(dS)
можно провести как в одном направлении,
так и
впротивоположном.Введемврассмотрениевекторориентированногомалогоэлементаповерхности
кулярнок(dS).Посколькумалыйэлемент(dS)по-верхности
является плоским, то вектор нормалиnк(dS)
можно провести как в одном направлении,
так и
впротивоположном.Введемврассмотрениевекторориентированногомалогоэлементаповерхности
![]()
![]() ,равного
,равного
-
dSdSn.
(5)
 гдеdSплощадьмалогоэлемента(dS)поверхности(S).
гдеdSплощадьмалогоэлемента(dS)поверхности(S).
Тогдапотоком(элементарным)
dE
векторногополя
EE(r)
через
dEE,dSE,ndSEcosdSEndS, |
(6) |
 малыйориентированныйэлементповерхностиназываетсячисло,равноеска-лярномупроизведениювекторовEиdS:
малыйориентированныйэлементповерхностиназываетсячисло,равноеска-лярномупроизведениювекторовEиdS:
гдеαугол междувекторамиEиn;
 EnE,nEcos–проекцияEнанаправление
единичноговектора
EnE,nEcos–проекцияEнанаправление
единичноговектора
нормалиn(или ).
Пустьвобластивекторногополя
EE(r)
находитсягладкаяиликусоч-
но-гладкая поверхность (S) конечных размеров (рис. 1).Ориентированнойявля-ется гладкая двусторонняя поверхность (S), в каждой точке которой задан еди-ничныйвекторn,направленныйпонормаликоднойизсторонэтойповерхно-
сти.ПотокΦЕвекторногополяEErчерезпроизвольнуюориентирован-
EE,dSE,ndS, (S) (S) |
(7) |
 нуюповерхность(S)–
эточисло,равноезначениюповерхностногоинтеграла
нуюповерхность(S)–
эточисло,равноезначениюповерхностногоинтеграла
![]()
 где n–векторориентированногомалогоэлемента(dS)поверхности(S);
где n–векторориентированногомалогоэлемента(dS)поверхности(S);
dSплощадьмалогоэлемента(dS)поверхности(S),впределахкотороговекторноеполе можносчитатьоднородным;
n–единичныйвекторнормаликмаломуэлементу(dS)поверхности(S).
В СИ[ΦE]= В·м.
EE,ndSEcosdSEndS, (S) (S) (S) |
(8) |
 Сучетомопределенияскалярногопроизведениявекторовпоток(7)век-торногополя
равен
Сучетомопределенияскалярногопроизведениявекторовпоток(7)век-торногополя
равен
гдеαуголмеждувекторамиEиn(рис.1);
 EnEcos–
проекцияEна
направление единичного вектора
нормалиn.Согласно
определению(7)потокΦЕ–величинаалгебраическая,т.к.онможетприниматьположительныезначения(ΦЕ>0),отрицательныезначения
EnEcos–
проекцияEна
направление единичного вектора
нормалиn.Согласно
определению(7)потокΦЕ–величинаалгебраическая,т.к.онможетприниматьположительныезначения(ΦЕ>0),отрицательныезначения
(ΦЕ<0)илибытьравнымнулю(ΦЕ=0)приE0.
 Формула
(7) определяет поток ΦЕчерез
двусто-роннююповерхность
(S)сточностью
дознака(«+»
или
Формула
(7) определяет поток ΦЕчерез
двусто-роннююповерхность
(S)сточностью
дознака(«+»
или
![]() «–»)
в зависимости от выбора стороны
поверхности, ккоторой
задаетсяединичный вектор нормалиn.
Еслиповерхность(S)ориентироватьзаданиемединичного
«–»)
в зависимости от выбора стороны
поверхности, ккоторой
задаетсяединичный вектор нормалиn.
Еслиповерхность(S)ориентироватьзаданиемединичного
векторанормали
n1кееверхнейстороне(рис.2),то
поток ΦЕ1в этом случае будет отличаться только зна-ком от потока ΦЕ2через ту же самую поверхность (S),ноориентированнуювыборомединичноговектора
E1E,n1dSEcos1dSEcos2dS (S) (S) (S) Ecos2dSE,n2dSE2. (S) (S) |
(9) |

 нормалиn2книжнейстороне(n2n1):
нормалиn2книжнейстороне(n2n1):
 В
случаезамкнутойповерхности (сферы,
поверхности параллелепипедаили
любой другой ограничивающей объемное
тело поверхности) единичныйвектор
нормалиnпроводится
квнешней сторонеэтой поверхности,
т. е.
нару-жуограничиваемойеюпространственнойобласти.Дляобозначенияповерх-
В
случаезамкнутойповерхности (сферы,
поверхности параллелепипедаили
любой другой ограничивающей объемное
тело поверхности) единичныйвектор
нормалиnпроводится
квнешней сторонеэтой поверхности,
т. е.
нару-жуограничиваемойеюпространственнойобласти.Дляобозначенияповерх-
ностногоинтегралапозамкнутойповерхности(S)используетсясимвол
ПотокΦЕвекторногополя
EE(r)
черезпроизвольнуюориентирован-
 нуюповерхность(S)прямопропорционаленразностичиславыходящихNвыход
нуюповерхность(S)прямопропорционаленразностичиславыходящихNвыход
E~NвыходNвход. |
(10) |
изэтойповерхностиивходящихNвходвнеесиловыхлинийэтогополя:

![]() Приэтомвыходящейизориентированнойпо-верхности
(S) является такая силовая линия,
направле-ние которой
в точке ее пересечения с (S)
образуетост-рыйугол
с единичным вектором нормалиnк
этой по-верхности
(рис. 3). Если силовая линия пересекает
ори-ентированнуюповерхность(S)так,чтонаправлениелинии
образует с единичным вектором
нормалиnкэтой
поверхноститупойугол, то такая
силовая линияявляетсявходящей.
Приэтомвыходящейизориентированнойпо-верхности
(S) является такая силовая линия,
направле-ние которой
в точке ее пересечения с (S)
образуетост-рыйугол
с единичным вектором нормалиnк
этой по-верхности
(рис. 3). Если силовая линия пересекает
ори-ентированнуюповерхность(S)так,чтонаправлениелинии
образует с единичным вектором
нормалиnкэтой
поверхноститупойугол, то такая
силовая линияявляетсявходящей.
 Теорема
Гаусса для поля вектора
напряженностиEэлектрическогополяввакуумевинтегральнойформе:потоквекторанапряженностиEэлектрического
поля в вакууме через любуюзамкнутуюповерхность
(S)
равеналгебраической
сумме зарядовqохв,
охватываемых этой поверхностью,
делен-нойна
электрическуюпостояннуюε0:
Теорема
Гаусса для поля вектора
напряженностиEэлектрическогополяввакуумевинтегральнойформе:потоквекторанапряженностиEэлектрического
поля в вакууме через любуюзамкнутуюповерхность
(S)
равеналгебраической
сумме зарядовqохв,
охватываемых этой поверхностью,
делен-нойна
электрическуюпостояннуюε0:
-
(E,dS)1q .
охв
(S) 0
(11)
Принимая во внимание связь потока ΦЕполя вектораEчерез произволь-ную ориентированную поверхность (S) счислом пересекающихэту поверх-ностьсиловых линийданного поля(10),изтеоремыГаусса(11)следует:
если замкнутая поверхность охватывает электрические заряды, то потоквектора напряженности через эту поверхность отличен от нуля, а значит, общеечислосиловыхлиний,пересекающихэтуповерхностьнеравнонулю,т.е.Nвых≠Nвход;
есливнутрипространственнойобласти,ограниченнойзамкнутойповерх-
ностью заряды отсутствуют, то число выходящих линий равно числу линийвходящихNвых=Nвход.
ПоэтомусодержательныйсмыслтеоремыГауссадляполявекторанапряженностиEэлектрического поля в вакууме в интегральной форме заклю-чается в следующем: в общем случае силовые линии электрического поля неявляются замкнутыми – они начинаются на положительных электрических за-рядах и оканчиваются наотрицательных.
![]()
 Гладкая
или кусочно-гладкая замкнутая кривая
(контур) считаетсяориен-тированной,
если вдоль нее выбрано направление
обхода, т. е. в каждой
точкеэтойкривойзаданединичныйвектор(1),направленныйпокасательнойк
Гладкая
или кусочно-гладкая замкнутая кривая
(контур) считаетсяориен-тированной,
если вдоль нее выбрано направление
обхода, т. е. в каждой
точкеэтойкривойзаданединичныйвектор(1),направленныйпокасательнойк
кривой всторонуобхода.
ЦиркуляцияΓЕвекторногополя
EE(r)
вдользамкнутойориентиро-
EE,dE,d, (L) (L) |
(12) |
 ваннойкривой(L)–эточисло,равное
значениюлинейногоинтеграла:
ваннойкривой(L)–эточисло,равное
значениюлинейногоинтеграла:
где
векторориентированногомалогоэлементаза-

 мкнутойкривой(L)(рис.4);
мкнутойкривой(L)(рис.4);
d![]() –длинамалогоэлемента(d
)замкнутойкривой(L),впределахкотороговекторноеполеможносчитатьоднородным;
–длинамалогоэлемента(d
)замкнутойкривой(L),впределахкотороговекторноеполеможносчитатьоднородным;
единичный вектор касательной к кривой (L) в некото-ройточкеэлемента(d ),понаправлениюсовпадающийснаправлениемобходавдоль(L).
В СИ[ΓE]= В.
 Сучетомопределенияскалярногопроизведениявекторовциркуляция(12)
векторногополя
равна
Сучетомопределенияскалярногопроизведениявекторовциркуляция(12)
векторногополя
равна
-
EEcosd Ed,
(L) (L)
(13)
гдеαуголмеждувекторамиEи(рис.4);

 EE,Ecos–проекцияEнанаправлениеединичноговекторакаса-
EE,Ecos–проекцияEнанаправлениеединичноговекторакаса-
![]() тельнойиливектораориентированногомалогоэлемента
тельнойиливектораориентированногомалогоэлемента
кривой(L).
РаботаАсилыFэлектрическогополяпридвижениивнемточечногоза-рядаqпозамкнутойтраектории(L),равнапроизведениюэтогозарядаqнацир-
куляциюΓЕвекторногополянапряженности
EF(r)
 q
q
вдользамкнутойориен-
 тированнойкривой(L),совпадающейстраекториейдвиженияданногозаряда:
тированнойкривой(L),совпадающейстраекториейдвиженияданногозаряда:
-
FqE
AF,dr qE,dqE,dqE.
(L) drd (L) (L)
(14)
E,d0. (L) |
(15) |
Теорема о циркуляции вектора напряженностиEэлектростатиче-ского поля в интегральной форме: циркуляция вектора напряженностиEэлектростатическогополя вдоль любой замкнутой ориентированной кривой (L)всегдаравна нулю:

С учетом (14) из теоремы о циркуляции (15) получается, что работа силэлектростатическогополяпридвижении внемточечного зарядаqпозамкнутой
траектории(L)всегдаравнанулю.Следовательно,силыэлектростатическогополяявляютсяконсервативными.
