Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный педагогический университет им. А.И. Герцена

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mathematics_part_1_hamov

.pdf

Скачиваний:

Добавлен:

12.02.2015

Размер:

1.28 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

деляемой собственными единичными перпендикулярными векторами X10 , X 20 .

Замечания. 1. Вектор столбец	x	и вектор строка X {x1 ; x2 }
Замечания. 1. Вектор столбец	X =	и вектор строка X {x1 ; x2 }
	1
	x2

есть различные обозначения одного и того же вектора на плоскости.

2. Несмотря на то, что для любой матрицы T , столбцы которой есть координаты собственных векторов, выполняется равен-

ство T		λ		0	,	матрицей перехода от прямоугольной сис-
ство T	−1	AT =	1		,	матрицей перехода от прямоугольной сис-
	−1		1	λ2
			0	λ2

темы координат (x 0 y) к прямоугольной системе координат (x′0 y′), определяемой собственными векторами, является лишь та матрица, столбцы которой — координаты единичных собственных векторов.

Матрица A определяет линейное преобразование (5.6; 5.7) и при переходе от системы (x 0 y) к системе (x′0 y′), определяемой собственными векторами, матрица линейного преобразования будет иметь вид A′ = T −1 AT , а по формуле (5.14) эта матрица будет диагональной:

A = T			λ		0		(5.15)
A = T	−1	AT =		1		.	(5.15)
′	−1			1	λ2
				0	λ2
Пример 5.6. Найти собственные числа и собственные векто-
ры матрицы		2		3		Преобразовать	матрицу A к диаго-
ры матрицы	A =				.	Преобразовать	матрицу A к диаго-
			3	10
			3	10

нальному виду.

Решение. Составляем характеристическое уравнение мат-
рицы		A	и	решаем его:			(2 −λ)	3	= 0	(2 −λ)(10 −λ) −9 = 0

							3	(10 −λ)
λ2	−12λ +11 = 0 . Получаем					собственное				значения матрицы
λ1 =1,	λ2	=11. Для каждого собственного значения находим собст-
венный вектор.
При λ1			=1	собственные векторы являются решениями одно-
родной		системы: x1 +3x2			= 0	<=>		x1 +3x2 = 0		<=> x1 = −3x2 , x2 —
				3x1 +9x2	= 0

111

свободная переменная, полагая

=1, получим x1 = −3;

таким об-

разом собственный вектор

−3

При

λ2

=11

собственные

векторы

—

решения

системы:

−

9x +

<=>

3x1 − x2

= 0

<=>

= 3x1 ,

полагая

=1,

получим

3x1 − x2

= 3 и собственный вектор X 2

Преобразующая матрица имеет вид

−3

T =

T −1 AT = −

−1

2 3 −3 1 1 0

−

−1

3 10 1 3 0 11

Единичные

собственные

векторы

данной

матрицы:

−3

−3 1

1 ,

X10

10 ,

X 20 =

10 ,

преобразующая

матрица

T =

1 3

1 0

осуществляет переход от системы

T0−1 AT0 =

и матрица

координат

(x 0 y)

к системе

(x′0 y′),

определяемой единичными

векторами

X10 , X 20 .

Задания для самостоятельной работы

1. Найти собственные числа и собственные векторы квад-

ратной матрицы A и преобразовать ее к диагональному виду:

а)

−3

49 −7

;

в)

0 6

A =

; б)

A =

−3

−7

6 5

Ответы: а) Собственные числа

λ1

= 2, λ2

= 8;

собственные

векторы (один из наборов)

X 2

−1

соответственно

1 =

−

единичные собственные векторы

. Преобра-

X10

X 20

зующая матрица (соответственно для первого и второго набора

112

									1	−	1
					1 −1				2	−	2
собственных				векторов)	1 −1		,	T0 =				,
собственных				векторов)	T =		,	T0 =				,
						1			1		1
					1	1			1		1
									2		2
									2		2
T −1 AT = T −1 AT	2		0
T −1 AT = T −1 AT	=			.
o 0		0	8
		0	8

			б)		Собственные								числа			λ1		= 0,	λ2	= 50; собственные векторы
																			1			7
			1				−7														−
X1		=	1		,	X 2	−7												50 ,		X 20 =	50 .
X1		=			,	X 2	=		, единичные X10 =										50 ,		X 20 =	50 .
				7					1										7			1

																			50			50
			Преобразующая матрица															1 −7			— для первого набора и
			Преобразующая матрица														T =				— для первого набора и

																		7		1
				1		−	7
				50		−	50
T 0=				50			50		— для набора из единичных векторов.
				7			1
				50
				50			50
			Тогда				T −1 AT = T0−1 AT0							0		0
			Тогда				T −1 AT = T0−1 AT0							=			.
															0	50
															0	50
			в)		Собственные числа											λ1		= 9, λ2		= −4.	Собственные векторы
X1		=		2	,		X 2			−3				Единичные						собственные			векторы
X1		=			,		X 2		=		.			Единичные						собственные			векторы
										2
				3						2
X	0	=		1		2	, X	0	=	1	−3
X	1	=					, X	2	=				.
	1							2		13		2
				13		3				13		2
																		2	−3
																	T =
			Преобразующая матрица																		для первого набора соб-
			Преобразующая матрица															3		2	для первого набора соб-
												T		=	1	2		−3
												T		=	1
ственных векторов;												0			13				— для набора из единичных
ственных векторов;															13	3		2	— для набора из единичных
собственных											векторов.								Выполняются				равенства
T −1 AT				= T −1 AT =					9		0
T −1 AT				= T −1 AT =								.
					0		0			−	4
									0	−	4

113

§ 5. Приведение общего уравнения кривой второго порядка к каноническому виду

Рассмотрим квадратичную форму с двумя переменными

f (x, y) = a11 x2 + 2a12 xy + a22 y2 .

Матрицей данной квадратичной формы называют симметрическую матрицу, составленную из коэффициентов формы f (x y)следующим образом

a	a
11	a	12
A = a	a	22	.
12		22

Данная матрица определяет линейное преобразование (5.2) плоскости.

Если перейти от системы координат (x0 y) , в которой форма f (x y) задана, к системе (x′0 y′) , определяемой перпендикулярными собственными единичными векторами, то матрица данного линейного преобразования будет равна матрице T0−1 AT0 , которая

′		λ	0
′		1
A	=	0	λ2	.
ввиду равенства (5.15) есть диагональная матрица		0	λ2

Этой матрице в системе координат(x′0 y′) соответствует квадратичная форма: f ′(x′y′)= λ1x′2 +λ2 x′2 . Таким образом, при переходе от системы координат (x0y) к системе (x′0 y′) , определяемой единичными ортогональными собственными векторами с соответст-

вующими		собственными значениями			λ1, λ2 ,			выражение
a	x2 + 2a xy + a	22	y2	преобразуется в выражение	λ x	′2	+λ	x	′2	. В этом
11	12	22			λ x		+λ	x
					1		2

случае говорят, что квадратичная форма приведена к каноническому виду.

Пример 5.7. Привести к каноническому виду следующие уравнения кривых второго порядка:

а) 2x2 −4xy +5y2 = 6

б) 2x2 +12xy −7 y2 + 20 = 0

в) 25x2 −14xy +25y2 +64x −64 y −224 = 0 г) x2 −2xy + y2 +6x −14 y +29 = 0 .

114

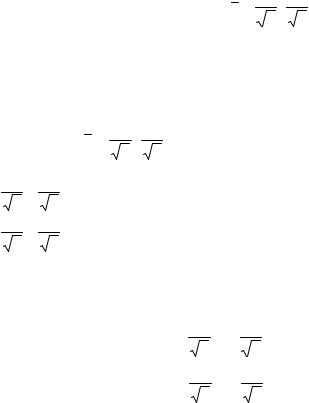
Решение:

а) составляем

матрицу

квадратичной формы,

−2

стоящей в левой части уравнения

A =

Составляем для

−

матрицы А характеристическое уравнение и решаем его:

(2 −λ)

− 2

= 0 <=> λ2

−7λ + 6 = 0

<=>

=1, λ

= 6.

(5 −λ)

− 2

Находим собственные векторы. Для λ1 =1

получаем систему

x1 −2x2 = 0

−2x1 + 4x2 = 0

<=>x

−2x

= 0

один из собственных векторов, соответствующих собственному значению

		2	;	1
λ1 =1, e1 {2; 1},	e1′	5		5	.		λ1 = 6 получаем
	нормируем его					Для

систему

−4x1 −2x2 = 0
−2x1 −			x2 = 0			<=> −2x − x				2	= 0,	собственный			вектор	e	2	{−1; 2},
									1	2		собственный			вектор		2
							−1	;	2
нормированный						e2′	5	;	.		Преобразующаяся				матрица			имеет
нормированный							5		5		Преобразующаяся				матрица			имеет
		2	−1
		5		5
T	=	5		5
0		1	2
вид		5
вид		5		5 . Формулы преобразования получаем по форму-
	x		= T	x′		:
			= T			:
ле (5.5) y			0	y	′						2		1
									x	=	2	x′−	1	y′
											5		5
											1		2
									y	=	1	x′+	2	y′
											5		5

Уравнение линии в новой системе координат, определяе-

	имеет вид: x′	2	+ 6 y′	2			x′2		y′	2
мой векторами e1′, e2′					= 6	<=>		+			=1 (эл-
							6		1

липс, рис. 5.3).

115

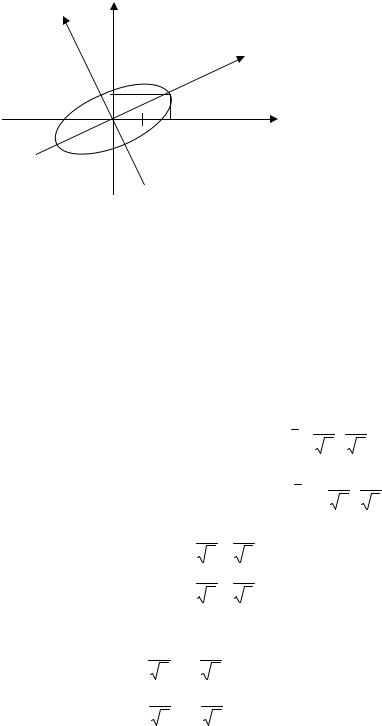
y′

x′

Рис. 5.3

б) матрица квадратичной формы

−7

. Характеристи-

ческое уравнение:

2 −λ

= 0 <=> x2 +5λ −50 = 0,

λ = 5, λ

= −10.

6 −7 −λ

Находим собственные векторы: для λ1 = 5 получаем систему

−3x1 + 6x2

= 0

<=> − x1 + 2x2

= 0, e1 {2, 1},

;

−12x2

e2′

6x1

= 0

5 5

;

12x1 + 6x2

= 0

<=> 2x1

+ x2

= 0,

e2 {−

1, 2},

;

e2′ −

для λ2 =10 : 6x1 +3x2

= 0

−1

Преобразующая матрица

5 . Формулы преобразо-

вания:

x =

x′

−

y′

y =

x′

y′

5 .

Уравнение линии в системе координат, определяемой векто-

рами e1′, e2′, имеет вид:

x′2

−

y′2

= −1

(гипербола, рис. 5.4).

116

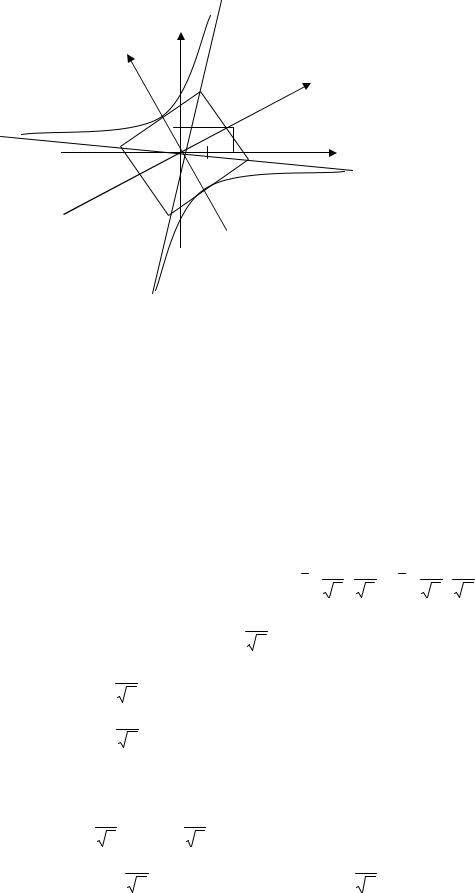
y
y'
	x'
1
0	2
0	x

Рис. 5.4

в) выражение 25x2 −14xy + 25y 2 в левой части уравнения является квадратичной формой. Приводим ее к каноническому виду. Корни характеристического уравнения

(25 −λ)

−7

= 0

λ1 =18, λ2

= 32.

−7

(25 −λ)

;

−1

;

Единичные собственные векторы

e1′

e2′

Преобразующая матрица

	1	(x′	− y′)
x =	2	(x′	− y′)
	2
	1
	1	′	′
системе (x′0 y′): y =	2	(x	+ y	).

уравнение

T	= 1	1	−1
				.
0	2		1
		1		Формулы перехода к

Подставляем данные формулы в

18x′2 +32y′2 + 642 (x′− y′)− 642 (x′− y′)− 224 = 0 <=>

<=>18x′2 +32y′2 −1282 y′− 224 = 0 <=> 9x′2 +16y′2 − 642 y′−112 = 0.

117

Далее, выделяем в левой части полный квадрат и осуществляем параллельный перенос системы (x′0 y′):

9x′	2					2	−	4		= 0.
9x′			+16 y′				−	2	y′+ 2 −144	= 0.
								2
9x′	2					−		2	2
9x′			+16 y′			−			=144.
								2
′		′		2			и переходим к системе координат
Обозначим X = x ; Y = y			−	2			и переходим к системе координат
′				O′				2		′
′				O′	0;					′
( XO Y ) с центром в точке								2	(координаты точки O , в систе-

ме x′0y′), в которой уравнение линии примет канонический вид

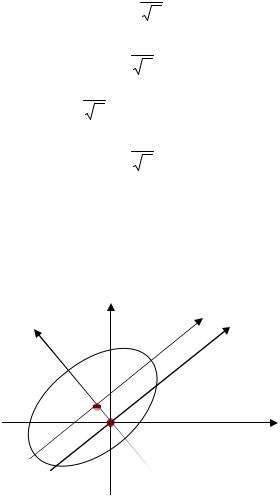
	X 2		Y 2
		+			=1
16		+	9		=1	(эллипс, рис.5.5)
16			9			(эллипс, рис.5.5)
	Y			y		X x′
	Y					X x′
y′
				0′
				0		x

Рис. 5.5

г) Приводим квадратичную форму x2 − 2xy + y2 к каноничес-

кому виду. Ее матрица			1	−1		. Находим корни характери-
кому виду. Ее матрица		A =				. Находим корни характери-
			−1	1
			−1	1
стического уравнения		(1 −λ )	−1	−λ)	= 0,		где λ = 0,	λ	2	= 2 .
стического уравнения		(1 −λ )	−1		= 0,		где λ = 0,	λ		= 2 .
	−1		(1				1

118

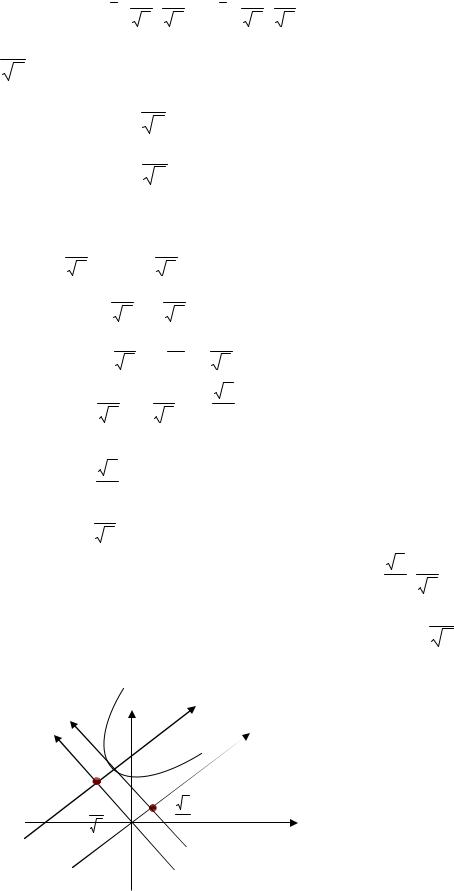
Собственные	векторы							e1′ 1							;	1		, e2′ 1 ;							1	. Преобразующая
													2			2								2	2
матрица T =	1	1 −1				, формулы преобразования:
матрица T =	1					, формулы преобразования:
0	2
	2	1		1
														1		(x′ − y′)
							x =								2	(x′ − y′)
															2
														1		(x′+ y′).
														1
							y =								2
															2
Подставляя в данное уравнение, получим
	2 y		′2	6			′	− y			′	)−			14		(x		′			′	)+ 29 = 0			<=>
	2 y			+ 2 (x				− y				)−				2	(x			+ y			)+ 29 = 0			<=>
					′2					8			′			20				′
	<=>			2 y			−			2 x				−			2	y			+ 29			= 0	<=>
	<=>					2	−		10				y′+			25				=		8		x′− 4		<=>
	<=>			2 y′			−			2			y′+			2				=		2		x′− 4		<=>
										2						2						2
	<=>						5 2						=		4							2
	<=>			y′−									=				x′−							.
								2								2						2
								2								2						2
Обозначая		X = x′−						2		,			осуществим параллельный перенос
Обозначая							2						осуществим параллельный перенос
		Y = y′−					5
							2

′ ′	)в систему	′		2		5		в
			′		;		,
системы (x 0 y		(XO Y )с центром в точке	O	2		2

которой уравнение линии примет канонический вид

(парабола, рис.5.6)

Y 2 = 42 X

y	X
Y
y′	x′
0′
5	2
2	2
0	x

Рис. 5.6

119

Задания для самостоятельной работы

1. Привести к каноническому виду уравнения кривых второго порядка. Изобразить линии на чертеже:

а) 3x2 − 2xy + 3y2 + 2x − 4 y +1 = 0 б) 5x2 +12xy − 22x −12 y −19 = 0 в) x2 − 2xy + y2 −10x − 6 y + 25 = 0 г) 4x2 − 4xy + y2 − 20 = 0

д) −3x2 +8xy + 3y2 = 0 .

Ответы: а) собственные числа: λ1 = 2, λ2 = 4 ;

		1	;	1		1	;	1
e1′			;		e2′ −	2	;
собственные векторы:		2		2 ,		2		2 .
Формулы преобразования:
	1		(x′ − y′)
x =		2	(x′ − y′)
		2
		1	(x′+ y′).
		1
y =		2
		2

Формулы параллельного переноса системы (x′0 y′):

	= x′−			1
X	= x′−			2
			2	2
		′		3			′		1		3
	= y	′	−	3	,	0	′		1	;	3
Y	= y		−		,	0				;		.
			4	2				2	2		4	2

Каноническое уравнение в системе (XO′Y ):

X 2	+	Y 2		=1.
3		3
			32	(эллипс).
16

б) Собственные числа: λ1 =9, λ2 = −4. Собственные векторы:

	3	;	2			2	;	3
e1′	13	;	13		e2′ −	13	;	13
	13		13	,		13		13	.

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.10.2018800.77 Кб3mater.doc
#
20.08.2019183.3 Кб4Materialy_iz_knig_Fundamentalnaya_biblioteka.doc
#
16.09.20192.37 Mб26Materialy_k_GEKu.doc
#
01.09.201973.73 Кб4materialy_k_zachjotu_po_psikhologii_zdorovja_20...doc
#
28.10.2018807.94 Кб4mater_pr.doc
#
12.02.20151.28 Mб16mathematics_part_1_hamov.pdf
#
12.02.201587.83 Кб40mat_dlya_DO1.docx
#
30.03.201639.2 Кб9Mertvye_doktora_ne_lgut.docx
#
23.09.2019640.51 Кб12method.doc
#
17.08.2019119.3 Кб5Metod-kursovik2007-2012.doc
#
07.12.20194.61 Mб1metodicheskie-rekomendacii-zd-v-ye-doc131315611...doc