mathematics_part_1_hamov

Математика

Часть I. Линейная алгебра и аналитическая геометрия: Учебное пособие

Санкт-Петербург

2004

ПРЕДИСЛОВИЕ

Пособие предназначено для студентов факультетов физики, химии, биологии, географии, технологии и предпринимательства.

Впервой части содержится материал, относящийся к разделу линейной алгебры и аналитической геометрии. В ней изложены: элементы теории матриц и определителей; методы решения систем линейных уравнений; основы аналитической геометрии на плоскости, векторной алгебры, аналитической геометрии в пространстве на базе векторной алгебры; метод приведения уравнения кривой второго порядка

кканоническому виду на основе линейной алгебры. Материал распределен на пять глав. В каждой главе приводятся: теоретический материал, в котором доказательства теорем и утверждений приведены выборочно; основные формулы, используемые для решения задач; подробно разобранные примеры; наборы задач для самостоятельной работы. В пособии имеются приложения с комплектами задач для проведения проверочных, контрольных работ или для выдачи индивидуальных заданий.

При самостоятельной работе с данным пособием перед тем, как приступить к решению задач, рекомендуется внимательно прочитать теоретические сведения параграфа и рассмотреть разобранные там примеры.

Нумерация определений, теорем, формул и примеров проведена по главам, при этом в приведенном номере первая цифра означает номер главы, а последующие цифры — порядковый номер в главе. Например, запись «Определение 1.3» означает, что определение находится в первой главе, а 3 — его порядковый номер в главе.

Вучебном пособии не приводятся доказательства некоторых теоретических положений. При необходимости ознакомления с ними рекомендуем обратиться к литературе:

Баврин И И. Курс высшей математики. — М., 1992. Шипачев В.С. Высшая математика. — М., 1996.

Мантуров О.В. Н.М. Матвеев. Курс высшей математики. — М., 1986.

3

Глава I. МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

§ 1. Матрицы. Действия над матрицами

Определение 1.1. Матрицей размера m ×n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов

Числа, составляющие матрицу, называются ее элементами. Элементы матрицы будем обозначать буквами с двумя индексами. Например, aij . В этом обозначении первый индекс — i ука-

зывает номер строки, а второй — j указывает номер столбца, на пересечении которых находится этот элемент. Для матрицы будем использовать обозначение

A = (aij ) (i =1, 2,...,m; j =1, 2,..., n).

Если m = n , то есть число строк матрицы равно числу ее столбцов, то матрица называется квадратной матрицей порядка n . Это матрица вида

Диагональ квадратной матрицы, идущая от левого верхнего к правому нижнему углу, то есть составленная из элементов a11 , a22 ,....ann , называется главной диагональю матрицы.

4

Матрица, не являющаяся квадратной, называется прямоугольной.

Единичной матрицей порядка n называется квадратная матрица порядка n , у которой все элементы главной диагонали равны 1, а все элементы вне этой диагонали равны нулю. Для обозначения единичной матрицы используется буква E .

Пример 1.1.

Пример 1.3.

E = 1 0 — единичная матрица второго порядка;

0 1

на одинаковых местах.

Матрицы можно складывать, вычитать, умножать на число и друг на друга.

Определение 1.2. Суммой двух матриц A = (aij ) и B = (bij ) размера m ×n называется матрица C = (cij ) размера m ×n , такая что

cij = aij +bij (i =1, 2,...,m; j =1, 2,..., n).

Сумма матриц A и B обозначается символом A + B .

5

m ×n , элементы которой определяются следующим равенством

6

сумме произведений соответствующих элементов i -й строки матрицы A и j - го столбца матрицы B , то есть

cij = ai1b1 j + ai2b2 j +K+ aik bkj (i =1,2,K, m; j =1,2,K, n).

Используется обозначение: C = AB .

Замечание. При умножении матриц количество столбцов первой матрицы обязательно должно совпадать с количеством строк второй матрицы.

7

Замечание. Если матрица A имеет размерность m ×k , а матрица B — размерность k ×m, то можно найти как A B, так и B A. Однако, вообще говоря, AB ≠ BA.

При умножении квадратной матрицы A n -го порядка на единичную матрицу такого же порядка имеем: AE = A и EA = A, то есть при умножении матриц единичная матрица обладает таким же свойством, как число 1 при умножении чисел.

Этим и объясняется ее название «единичная».

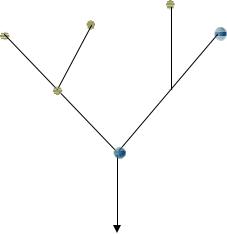
В географии широкий интерес представляет применение матриц при изучении географических сетей (речные сети, транспортные сети и т.д.). Рассмотрим для примера участок речной сети (рис. 1.1) в матричной форме относительно количества притоков (ребра), сходящихся в каждой точке их слияния (узловые точки)

E 4

C 3

6

K

7

Рис. 1.1

Для изображения речной сети матрица может быть составлена как с использованием ребер, так и узлов. Обозначим (см. рис. 1.1) ребра числами 1,2,3,4,5,6,7, а узлы буквами A,B,C,D,E,F,K,L.

В матрице ребер число 0 означает, что притоки непосредственно не соединяются, а 1 — что они соединяются; в матрице узлов число 0 означает, что узлы непосредственно между собой не связаны. Получим матрицы:

8

Если учесть течение воды, то матрицы примут вид:

Сумма по каждому столбцу дает общее количество притоков, впадающих в каждую реку. В данном случае по два притока в 3;6;7 и по два — в узлы C,E,K. Изменения речной сети легко представить путем сложения и вычитания матриц. Изложенный метод можно распространить на другие характеристики речной сети, расход воды, размер русла и т.д.

Задания для самостоятельной работы

Найти: а) A + B; б) A − B.

9