
- •Матрицы
- •Алгебра матриц
- •Вычисление обратной матрицы
- •Ранг матрицы
- •Системы линейных уравнений
- •Аналитическая геометрия
- •5 Видов уравнения на плоскости прямой.
- •Второй замечательный предел
- •Предел функции непрерывного аргумента
- •Первый замечательный предел
- •Непрерывность
- •Первая теорема Больцано-Коши
- •Локальные экстремумы функции
Линейная алгебра.
Определители (детерминант)
Назовем определителем число, записанное в виде квадратной таблицы чисел.
Ч![]()
![]()
![]()
![]()
![]() исло
элементов в строке (колонке) называют
порядком определителя.
исло
элементов в строке (колонке) называют
порядком определителя.
Для определителя справедливы 2 правила:
Это правило эквивалентных преобразований.
Правило раскрытия по строке (колонке).
Правило эквивалентных преобразований:
Если в определителе какую-то строку умножить на число не равное нулю (столбец) прибавить к другой строке (столбцу), то мы получим определитель эквивалентный данному.
П![]() ример:
ример:


![]()
Правило раскрытия по строке:
Каждый определитель порядка n может быть представлен в виде суммы произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
![]()
![]()
А![]()
![]()
![]()
![]()
![]()
![]() лгебраическим
дополнениемAij
к элементу aij
назовем
произведение (-1)i+jMij,
где M-
минор.
лгебраическим
дополнениемAij
к элементу aij
назовем
произведение (-1)i+jMij,
где M-
минор.
Минором, построенным по элементу aij , называется определитель порядка (n-1), полученный из исходного путем вычеркивания i строки и j столбца.
![]()
![]()
![]()
![]()
П![]()
 ример:
ример:
M![]()
 11=|1|
11=|1|
Если в каком-то определителе есть строка (колонка), состоящая из нулей, то определитель равен нулю.
Определитель 2-го порядка равен разности произведений к элементу главной диагонали (СЗ, ЮВ) и элементов побочной диагонали (СВ, ЮЗ)
П римеры:
римеры:
![]()

![]()





Матрицы
Матрицой называют прямоугольную таблицу чисел.
![]()

Алгебра матриц
![]()
![]()
![]()
![]()
![]()
![]()
Сложение:
![]()
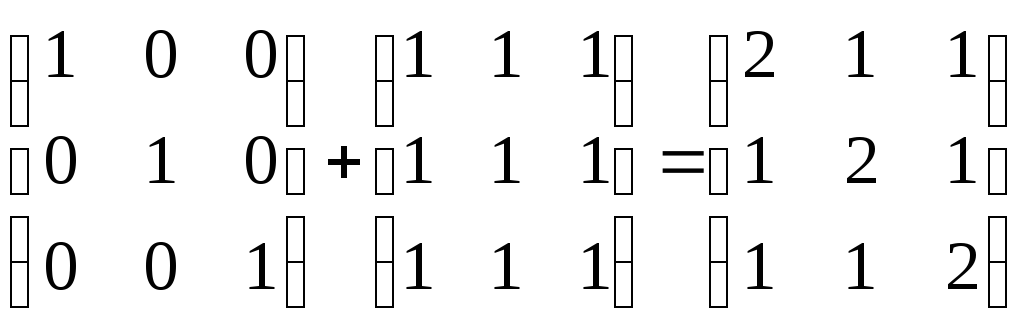
Умножение:
![]()
![]()
![]()
![]()
![]()
Правило согласованности размерности матриц при умножении:
Количество столбцов 1-го сомножителя равняется количеству строк 2-го.
Чтобы получить элемент произведения двух матриц ij мы должны умножить i строчку 1-го сомножителя на j столбец 2-го и результаты сложить.
П ример:
ример:
![]()
![]()
Е![]()
![]()
![]() -
единичная матрица
-
единичная матрица
Э то
квадратная матрица, у которой по главной
диагонали стоят единицы, а остальные
нули.
то
квадратная матрица, у которой по главной
диагонали стоят единицы, а остальные
нули.
![]()
![]() 1
1![]()
![]()
![]() 1=1+1+1=3
1=1+1+1=3
12=3
21=0
22=0
Для всякой квадратной матрицы можно посчитать определитель.
Е сли
главный определитель квадратной матрицы
ноль, то матрица называется выражденной.
сли
главный определитель квадратной матрицы
ноль, то матрица называется выражденной.
Чтобы умножить матрицу на число, надо каждый элемент этой матрицы умножить на это число.
Вычисление обратной матрицы
![]()
![]()

Доказательство:


![]()
![]()
![]()
![]()
![]()
![]()
A![]() 11=(-1)1+1*3=3
11=(-1)1+1*3=3
A12=-2
A21=-1
A22=1
Ранг матрицы
![]()
Р![]() анг
(rang)
А- размерность наибольшего отличного
от нуля определителя, содержащегося в
матрице А.
анг
(rang)
А- размерность наибольшего отличного
от нуля определителя, содержащегося в
матрице А.
Min (m,n)- максимально возможный порядок определителя.
П![]() ример:
ример:
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
Системы линейных уравнений
Это система, у которой m уравнений и n неизвестных
О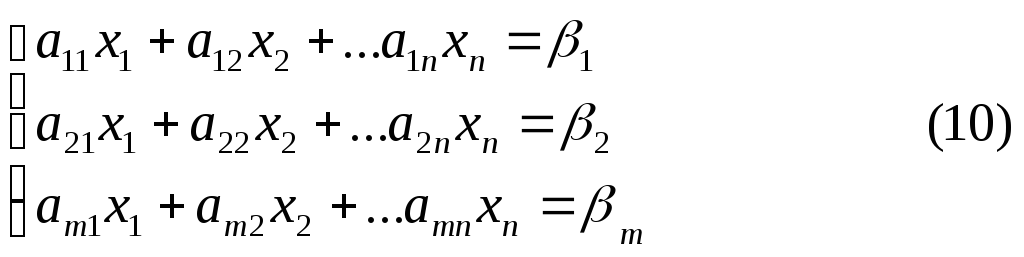 бщий
вид
бщий
вид![]() системы линейных уравнений
системы линейных уравнений
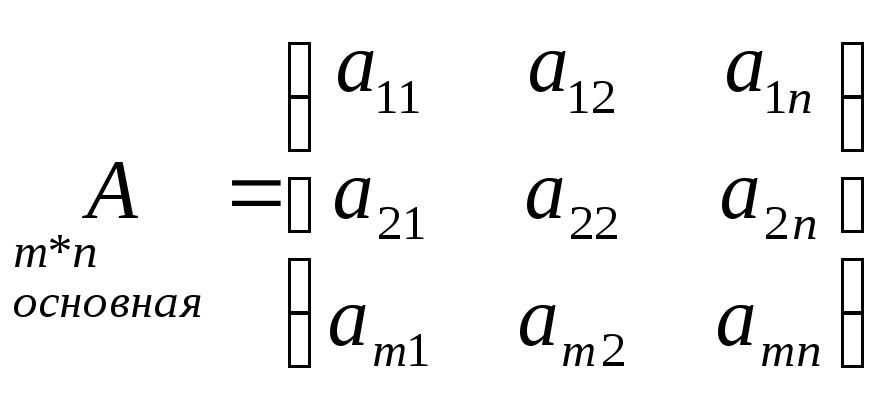

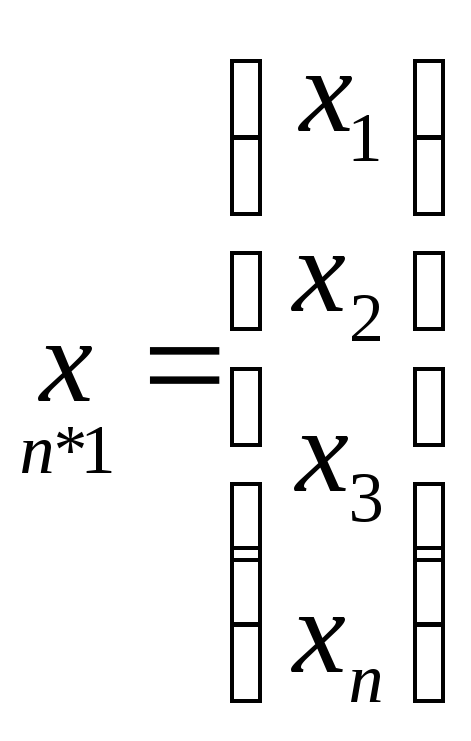

![]()
![]()
Матричная запись системы (10)
![]()
Д![]() опущения:
опущения:
А- квадратная, невырожденная
А-1Ax=A-1B x=A-1B (11) (решение системы 10)
Если количество неизвестных больше числа уравнений, то последнее (лишнее неизвестное) переходит в разряд параметров и переносится в правую часть.
Если основная матрица вырожденная, то отбрасывается последнее уравнение до тех пор, пока она не станет невырожденной.
Теорема Кронекера- Капелли:
С истема(10)
имеет решения тогда и только тогда,
когда ранг основной матрицы системы
совпадает с рангом расширенной матрицы
(rang
A=
rang
A),
если при этом эти ранги совпадают с
числом неизвестных n,
то решение единственно. Если меньше n,
то решений бесконечно много.
истема(10)
имеет решения тогда и только тогда,
когда ранг основной матрицы системы
совпадает с рангом расширенной матрицы
(rang
A=
rang
A),
если при этом эти ранги совпадают с
числом неизвестных n,
то решение единственно. Если меньше n,
то решений бесконечно много.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
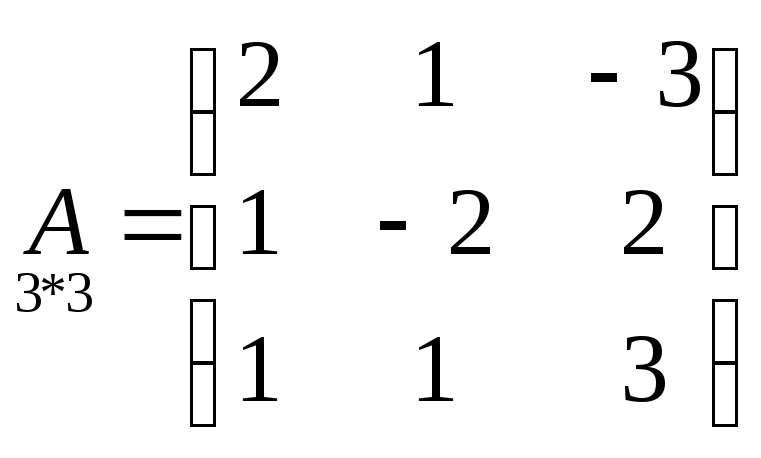
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Векторная алгебра
![]()
Y



 a2
a2

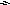 a
a

 0
a1
X
0
a1
X
Умножение вектора на число:
![]()
![]()
С![]()

![]() ложение
и вычитание:
ложение
и вычитание:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Умножение векторов:
а) Скалярное произведение:
![]()
![]()
к![]() оммутативно
оммутативно
![]()
б) Векторное произведение (3-х мерное):
![]()
![]()
![]()
![]()

![]()
![]() i
i![]() ,j,k-
орты осей координат
,j,k-
орты осей координат

![]()
![]()
![]()
![]()
![]()
![]()
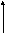
![]()
![]()
![]()
![]()
![]()



![]()

![]()
![]()
![]()
![]()

![]()
С![]() войство
антикоммутативности
войство
антикоммутативности

Геометрический определитель второго порядка равен длине векторного произведения векторов, составленных из строк данного определителя.
Геометрическое смешенное произведение:
О но
равно объему параллелепипеда, построенного
на исходных векторах.
но
равно объему параллелепипеда, построенного
на исходных векторах.
![]()
![]()
![]()
Аналитическая геометрия
5 Видов уравнения на плоскости прямой.
Уравнение прямой с угловым коэффициентом
Y=kx x=0 y=0
(0,0) (x1, kx1)
(x2, kx2)
Y=kx+b![]()
![]()
![]() (1)
(1)
Общие уравнения
![]()
Kx-y+b=0
A B C
Ax+By+C=0
![]() (2)
(2)
![]() Общее
уравнение прямой на плоскости
Общее
уравнение прямой на плоскости
У

 равнение
в отрезках
равнение
в отрезках
Ax+By=-C
![]()
![]()
![]()
![]() a b
a b
![]()
Уравнение прямой через две заданные точки
(x0, y0) (x, y)

![]()
![]()



![]()
![]()
Н


 ормальное
уравнение прямой
ормальное
уравнение прямой
y
![]()



![]()
![]()
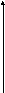

![]()
![]() 0
x
0
x
![]()
![]()
![]()
![]()
р![]()
![]() асстояние
от (0,0) доl
асстояние
от (0,0) доl
![]()
![]()

![]()
![]()
![]()
![]() -
угол между
и осью
-
угол между
и осью
z



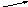
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Нормальное уравнение плоскости в пространстве
![]()
![]()

![]()
Нормальный вид уравнения плоскости в пространстве:
Ax+By+Cz+D=0 (7)
Уравнение прямой в пространстве или множество точек в пространстве задается двумя уравнениями плоскости в пространстве.
Дифференциальное исчисление
Теория пределов
Предел последовательности
X- область определения
Y- область значений
- для любого
- существует
- единственный
- следует
Ф![]()
![]() ункция-
закон, по которому для любого элемента
x
из множества X
существует единственный y
из множества Y.
ункция-
закон, по которому для любого элемента
x
из множества X
существует единственный y
из множества Y.

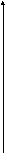 Y
Y



 y*
y*

 y*
y*

 x*
x*
x*
x*
R 0 X
 y**
y**
![]() не
функция
не
функция
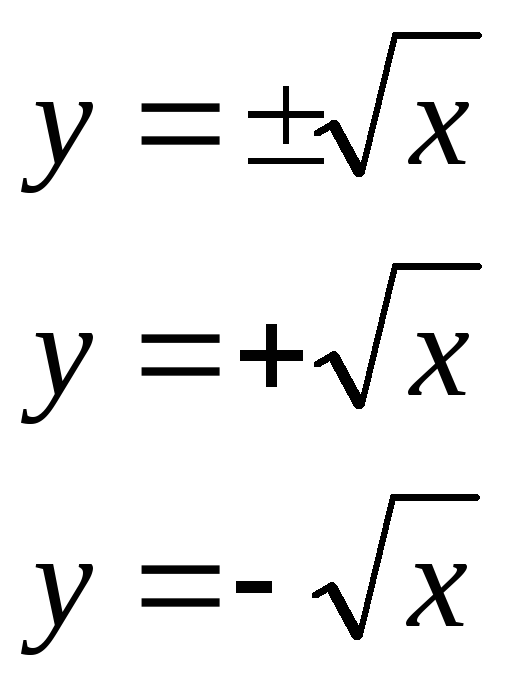
М![]()
![]() ножество
натуральных чисел
ножество
натуральных чисел
Множество натуральных чисел с нулем
М![]()
![]()
![]() ножество
целых чисел
ножество
целых чисел![]()
М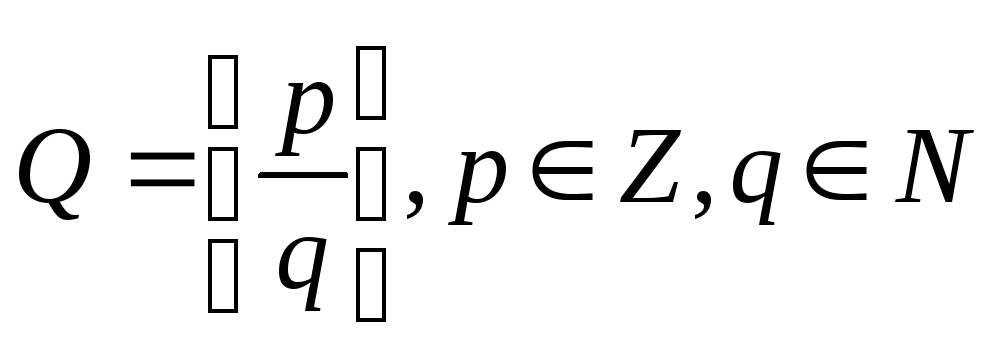 ножество
рациональных чисел
ножество
рациональных чисел
R![]()
![]() -
Множество всех периодических десятичных
дробей
-
Множество всех периодических десятичных
дробей
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Xn=(-1)n 1,-1,1,-1…- гармонический ряд, ряд Эйлера
Свойства последовательности, имеющих пределы.
1![]()
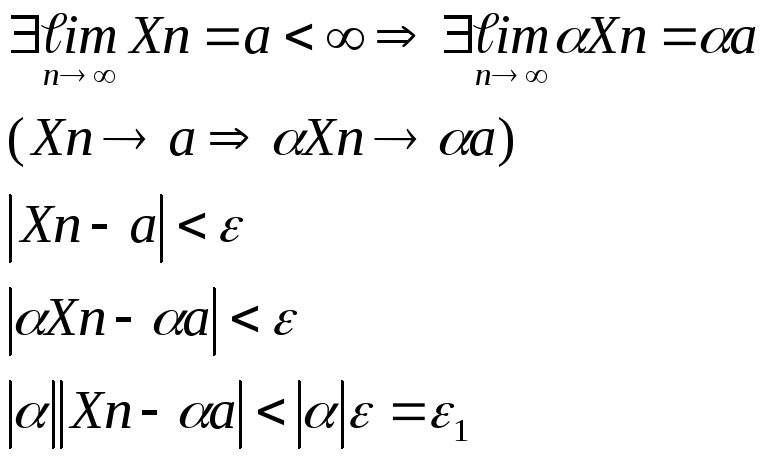 )
)
2 )
)
![]()
Д![]()
![]() оказать:
оказать:
![]()
![]()
![]()
![]()
3![]()
![]()
![]()
![]()
![]()
![]()
![]() )
)
![]()
![]()
![]()
![]()
Определение предела последовательности:
![]()
![]()
![]()
![]()
X![]()
![]() n
монотонно возрастает с строгом
(нестрогом) смысле
n
монотонно возрастает с строгом
(нестрогом) смысле
X
 n
монотонно убывает в строгом
(нестрогом) смысле
n
монотонно убывает в строгом
(нестрогом) смысле
![]()
![]()

![]()
X![]() n
ограничена,
если для всех n
n
ограничена,
если для всех n
![]()
X![]() n
ограничена сверху
n
ограничена сверху
![]()
X![]() n
ограничена снизу
n
ограничена снизу
![]()
Точкой верхней границы Xn supXn (infXn) называется наименьшая из верхних границ (наибольшая из нижних границ)
a=supXn
b![]() =infXn
=infXn
![]()
Теорема о пределе монотонной и ограниченной последовательности
Пусть последовательность Xn монотонно возрастает (убывает) и ограничена сверху.

X
![]()
![]()
![]()
![]() n
n
Существует конечный предел ограниченной последовательности
Доказательство:
Д![]()
![]()
![]() окажем,
что
окажем,
что
![]()
![]()

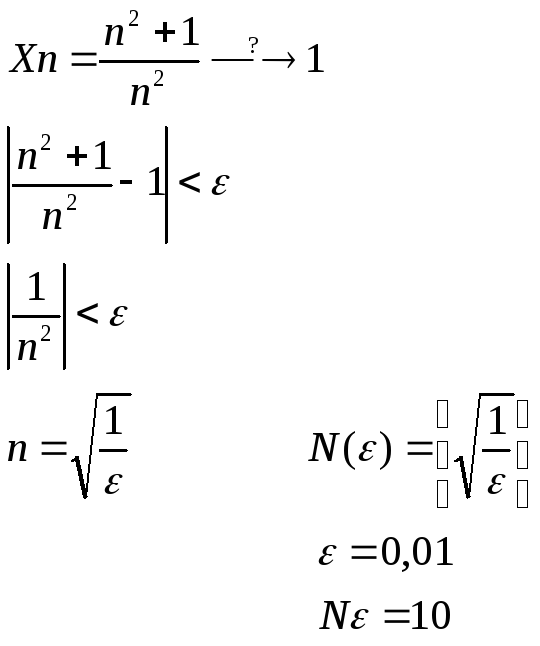

![]()
![]()
![]()
бесконечно большая величина
![]()
б![]() есконечно
малая величина
есконечно
малая величина
![]()
