Интегрирование по частям.

Если функции u = (x) и v = (x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше, поэтому здесь приводить его нет смысла.

Несобственные интегралы.

Пусть функция f(x) определена и непрерывна на интервале [a, ). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел , то этот предел называетсянесобственным интегралом от функции f(x) на интервале [a, ).

Обозначение:

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Пример.

-

не существует.

Несобственный интеграл расходится.

Пример.

- интеграл сходится

Теорема: Если для всех х (x  a) выполняется условие и интегралсходится, тотоже сходится и .

Теорема: Если для всех х (x  a) выполняется условие и интегралрасходится, тотоже расходится.

Теорема: Если сходится, то сходится и интеграл.

В этом случае интеграл называетсяабсолютно сходящимся.

Интеграл от разрывной функции.

Если в точке х = с функция либо неопределена, либо разрывна, то

Если интеграл существует, то интеграл-сходится, если интеграл не существует, то- расходится.

Если в точке х = а функция терпит разрыв, то .

Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то

Таких точек внутри отрезка может быть несколько.

Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.

Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур.

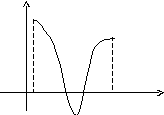
у

+ +

O a - b x

Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

Для нахождения суммарной площади используется формула .

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x², x = 2.

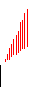
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:

(ед²)

Нахождение площади криволинейного сектора в полярной системе координат.

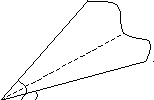
 = f()





О 

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид  = f(), где  - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а  - угол наклона этого радиус – вектора к полярной оси .

Площадь криволинейного сектора может быть найдена по формуле