61)Математическая модель потенциального риска.
66) Основные величины, входящие в математическую модель коллективного риска токсического поражения.
N-кол-во людей
Методика расчета коллективного риска токсического поражения.
Математическая модель коллективного риска фугасного поражения.
Основные величины, входящие в математическую модель коллективного риска фугасного поражения.
R(N)=Rind*N
N-кол-во людей
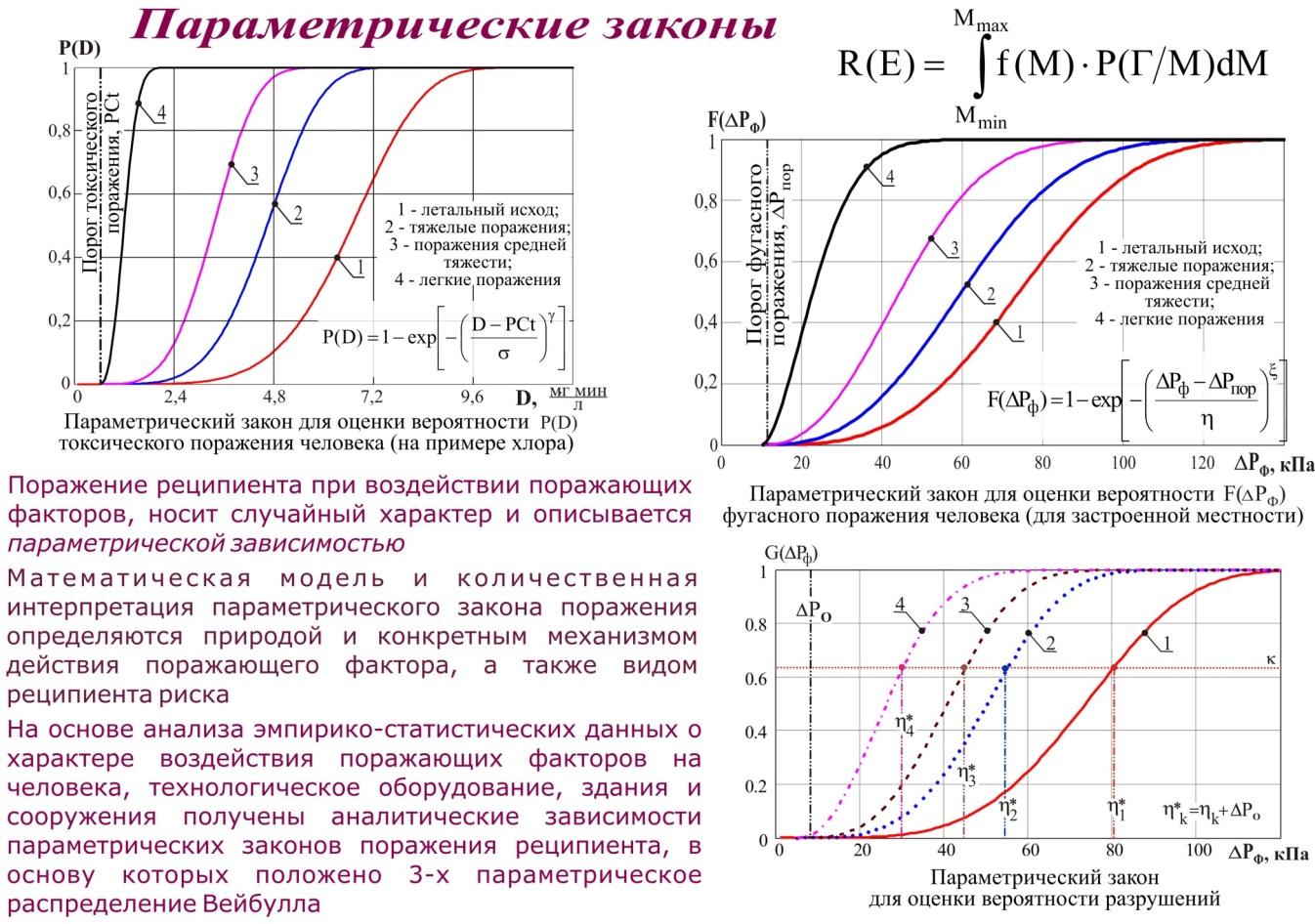
Распределение Вейбулла для оценки вероятности фугасного поражения человека.
Математические модели параметрического и координатного законов фугасного поражения индивидуума.
модели параметрического
ПАРАМЕТРИЧЕСКИЙ ЗАКОН ПОРАЖЕНИЯ
Вероятность поражения реципиента в рассматриваемой точке территории Р(Г) описывается распределением Вейбулла, которое принято называть параметрическим законом поражения реципиента.
КООРДИНАТНЫЙ ЗАКОН ПОРАЖЕНИЯ
Зная параметрический закон поражения человека Р(D), мы не можем судить о характере распределения потенциального риска на прилегающей территории.
Для решения данной задачи необходимо знать, как изменяется вероятность поражения человека по мере удаления от источника опасности, то есть от параметрического закона необходимо прейти к координатному закону поражения человека Р(Г).
Методика расчета коллективного риска фугасного поражения.
Математическая модель индивидуального риска.
ИНДИВИДУАЛЬНЫЙ РИСК
Основные величины, входящие в математическую модель индивидуального риска.
По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск
Rind = R(E)P(N)
Индивидуальный риск – частота поражения отдельного индивидуума (человека) в результате воздействия поражающего фактора.
Потенциальный риск на прилегающей к ОПО территории в пределах КВП не может быть равен нулю по определению, в то время как индивидуальный риск может изменяться от нуля до величины потенциального риска
(0 ≤ Rиндивидуум ≤ Rпотенциал)
Оценка вероятности нахождения индивидуума в данной точки рассматриваемой территории.
По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск
Rind = R(E)P(N)
Основные величины, входящие в математическую модель коллективного риска токсического поражения.
N-кол-во людей
Методика расчета коллективного риска токсического поражения.
Математическая модель коллективного риска фугасного поражения.
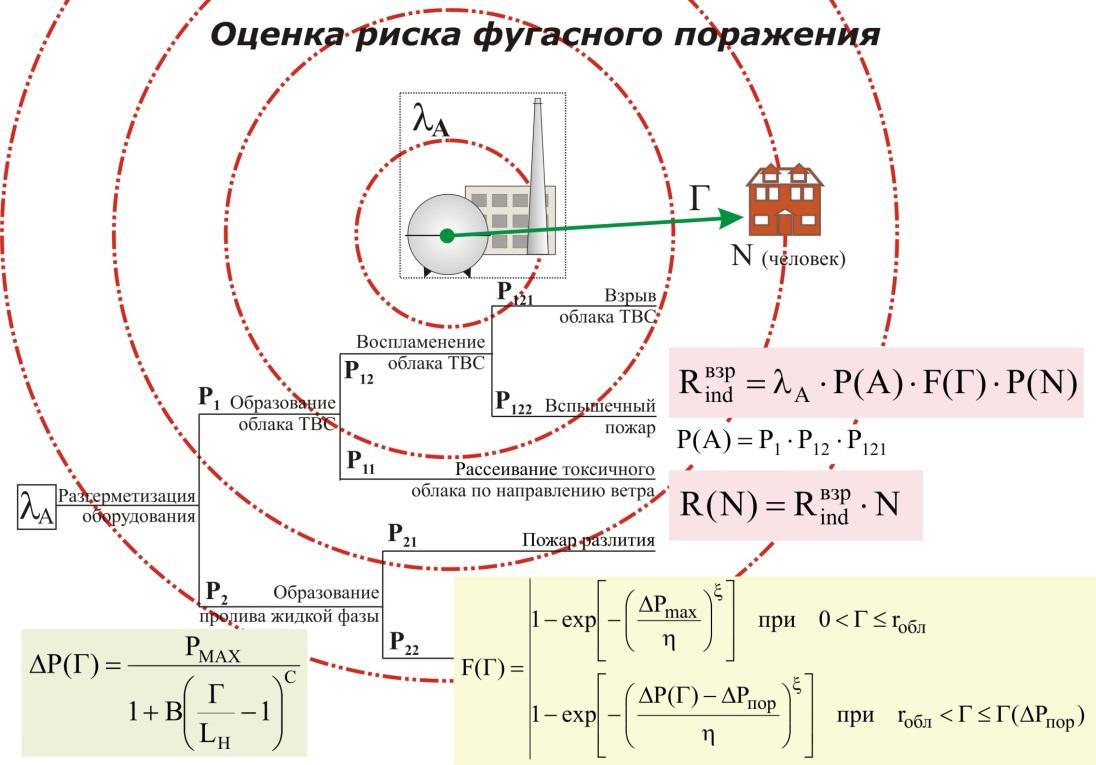
Основные величины, входящие в математическую модель коллективного риска фугасного поражения.
R(N)=Rind*N
N-кол-во людей
Распределение Вейбулла для оценки вероятности фугасного поражения человека.
Математические модели параметрического и координатного законов фугасного поражения индивидуума.
модели параметрического
ПАРАМЕТРИЧЕСКИЙ ЗАКОН ПОРАЖЕНИЯ
Вероятность поражения реципиента в рассматриваемой точке территории Р(Г) описывается распределением Вейбулла, которое принято называть параметрическим законом поражения реципиента.
КООРДИНАТНЫЙ ЗАКОН ПОРАЖЕНИЯ
Зная параметрический закон поражения человека Р(D), мы не можем судить о характере распределения потенциального риска на прилегающей территории.
Для решения данной задачи необходимо знать, как изменяется вероятность поражения человека по мере удаления от источника опасности, то есть от параметрического закона необходимо прейти к координатному закону поражения человека Р(Г).
Методика расчета коллективного риска фугасного поражения.
Математическая модель индивидуального риска.
ИНДИВИДУАЛЬНЫЙ РИСК
Основные величины, входящие в математическую модель индивидуального риска.
По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск
Rind = R(E)P(N)
Индивидуальный риск – частота поражения отдельного индивидуума (человека) в результате воздействия поражающего фактора.
Потенциальный риск на прилегающей к ОПО территории в пределах КВП не может быть равен нулю по определению, в то время как индивидуальный риск может изменяться от нуля до величины потенциального риска
(0 ≤ Rиндивидуум ≤ Rпотенциал)
Оценка вероятности нахождения индивидуума в данной точки рассматриваемой территории.
По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск
Rind = R(E)P(N)