ОТчет по Simulink
.docx
Цель работы:
-
Изучить приёмы моделирования систем автоматического управления в системе MatLAB.
-
Исследовать системы автоматического регулирования температуры печи сопротивления.
Введение
Система MatLAB (сокращение от MATrix LABoratory — МАТричная ЛАБоратория) является интерактивной системой для выполнения инженерных и научных расчетов, ориентированной на работу с массивами данных. Система использует математический сопроцессор и допускает возможность обращения к программам, написанным на языках FORTRAN, Си и C++.
Особенностью системы является то, что она содержит развитую встроенную матричную и комплексную арифметику. Система поддерживает выполнение операций с векторами, матрицами и массивами данных, реализует сингулярное и спектральное разложения, поддерживает работу с алгебраическими полиномами, решение нелинейных уравнений и задач оптимизации, интегрирование, решение дифференциальных и разностных уравнений, построение различных видов графиков, трехмерных поверхностей и линий уровня, моделирование систем автоматического регулирования. В ней реализована удобная операционная среда, позволяющая формулировать проблемы и получать решения в привычной математической форме, не прибегая к рутинному программированию.
Основным объектом системы MatLAB является прямоугольный числовой массив, который допускает комплексные элементы и ввод матриц без явного указания их размеров. Система позволяет решать многие вычислительные задачи за значительно меньшее время, нежели то, которое необходимо для написания соответствующих программ на языках FORTRAN, Basic и Си.
Система MatLAB выполняет операции с векторами и матрицами даже в режиме непосредственных вычислений без какого-либо программирования. Ею можно пользоваться как мощнейшим калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями могут использоваться такие сложные операции, как обращение матрицы, вычисление ее собственных значений и векторов, решение систем линейных алгебраических уравнений и много других. Однако основная отличительная черта системы — это легкость ее модификации и адаптации к конкретным задачам пользователя. Пользователь может ввести в систему любую новую команду, оператор или функцию и пользоваться затем ими так же просто, как и встроенными операторами и функциями. При этом, в отличие от языков программирования, таких как Basic, Pascal или Си, нет необходимости в их предварительном описании. Новые программы, функции и процедуры в системе MatLAB сохраняются в виде файлов, имеющих расширение .m. Это делает набор операторов и функций практически неограниченным.
В базовый набор слов системы входят: спецзнаки; знаки арифметических и логических операций; арифметические, тригонометрические и некоторые специальные математические функции; функции быстрого преобразования Фурье и фильтрации; векторные и матричные функции; средства для работы с комплексными числами; операторы построения графиков в декартовой и полярной системах координат, трехмерных поверхностей и т.д.
Система MatLAB имеет собственный язык программирования, напоминающий Basic. Запись программ в системе является традиционной и поэтому привычной для большинства пользователей персональных компьютеров. К тому же система дает возможность редактировать программы при помощи любого привычного для пользователя текстового редактора.
MatLAB имеет большие возможности для работы с сигналами, для расчета и проектирования аналоговых и цифровых фильтров, для построения их частотных, импульсных и переходных характеристик. Имеются в наличии и средства для спектрального анализа и синтеза, в частности, для реализации прямого и обратного преобразования Фурье. Благодаря этому система довольно привлекательна для проектирования электронных устройств и моделирования систем автоматического регулирования.
-
Приёмы моделирования систем автоматического управления в системе MatLAB.
Блок Signal Generator
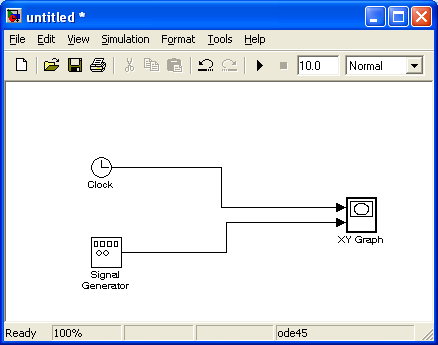
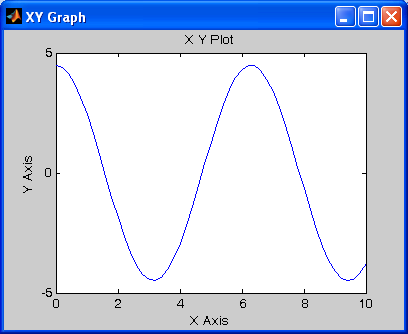
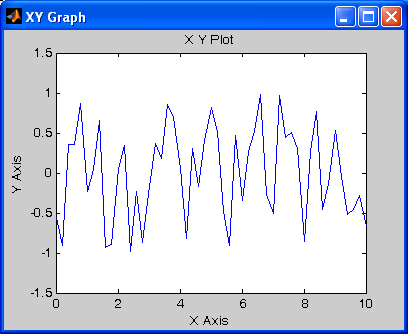
На рис. 1.1 показана простейшая S-модель, состоящая из блока Signal Generator и блока отображения XY Graph. На следующем рисунке (1.2) представлено содержимое блока отображения после проведения моделирования при таких параметрах настройки: вид колебаний — Sine; амплитуда — 4,5; частота — 1 Гц.
|
|
|
|
Рис 1.1 |
Рис 1.2 |
Блок Step
Блок обеспечивает формирование управляющего сигнала в форме ступеньки (или, как говорят, скачкообразного постоянного сигнала) (рис1.3). Установим следующие параметры настройки блока: Step time — 3,5, Initial value — -2, Final value — 3. После активизации моделирования (команда Start из меню Simulation) получим в окне Scope картину, представленную на рис. 1.4.
|
|
|
|
Рис 1.3 |
Рис 1.4 |
Блок Ramp
Блок формирует постоянно нарастающий сигнал и имеет следующие параметры настройки(рис 1.5):
• Slope - значение крутизны наклона прямой коси времени;
• Start time – время начала действия нарастающего сигнала;
• Initial output – значение сигнала в момент начала его действия.
|
|
|
|
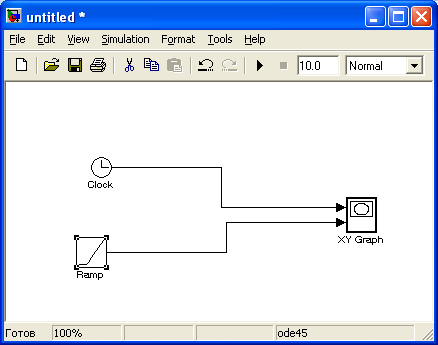
Рис 1.5 |
Рис 1.6 |
На рис. 1.6 проиллюстрировано применение блока Ramp при следующих значениях параметров: Slope – 1, Start time – 3, Initial output - -3.
Блок Sine Wave
Блок (рис 1.7) имеет следующие настройки:
• Amplitude – определяет амплитуду синусоидального сигнала;
•
Frequency
(rad/sec)
– задаёт частоту колебаний в рад/с ( );
);
• Phase (rad) – устанавливает начальную фазу в радианах;
• Sample time – определяет дискретность значений синусоидального сигнала.
На
рис. 1.8 представлен результат применения
блока со следующими параметрами:
Amplitude
– 4,5; Frequency
- 1 ;
Phase
-
;
Phase
-
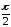 .
.
|
|
|
|
Рис 1.7 |
Рис 1.8 |
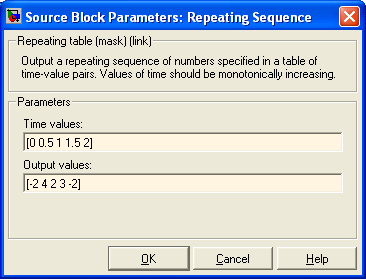
Блок Repeating Sequence
Этот блок (рис 1.9) содержит две настройки:
• Time values — вектор значений времени, в которых заданы значения выходной величины;
• Output values — вектор значений выходной величины, которые она должна принять в указанные в первом векторе соответствующие моменты времени.
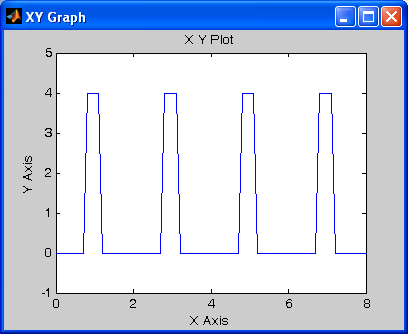
Блок обеспечивает генерирование колебаний с периодом, равным разности между последним значением вектора Time values и значением первого его элемента. Форма волны внутри периода представляет собой ломаную, проходящую через точки с указанными в векторах Time values и Output values координатами.
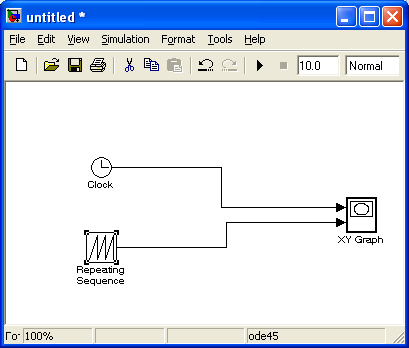
В качестве примера на рис. 1.11 приведено изображение процесса, сгенерированного блоком Repeating Sequence при параметрах настройки, указанных на рис. 1.10.
|
|
|
|
Рис 1.9 |
Рис 1.10 |
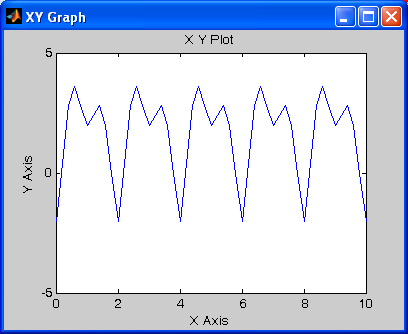
Рис 1.11
Блок Discrete Pulse Generator
Блок (рис 1.12) генерирует последовательности прямоугольных импульсов.
На рисунке 1.13 представлены параметры а на рис 1.14 выходной график.
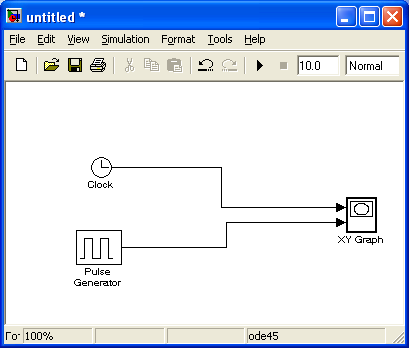
Рис 1.12
|
|
|
|
Рис 1.13 |
Рис 1.14 |
Блок Chirp Signal
Этот блок(рис1.15) генерирует синусоидальный сигнал единичной амплитуды и переменной частоты, причем частота колебаний изменяется во времени по линейному закону.
На рисунке 1.16
представлены параметры а на рис 1.17
выходной график.

Рис 1.15
|
|
|
|
Рис 1.16 |
Рис 1.17 |
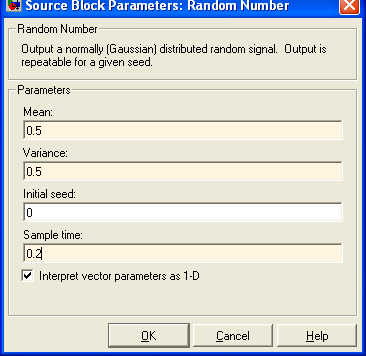
Блок Random Number
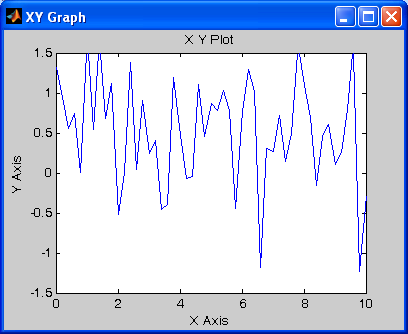
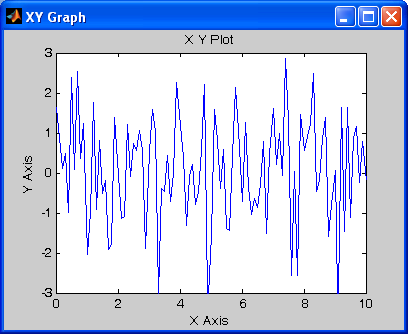
Блок Random Number (рис 1.18) обеспечивает формирование сигналов, амплитуда которых является случайной величиной, распределенной по нормальному закону с заданными параметрами.
На рисунке 1.19 представлены параметры а на рис 1.20 выходной график.

Рис 1.18
|
|
|
|
Рис 1.19 |
Рис 1.20 |
Блок Uniform Random Number
Этот блок(рис 1.21) формирует сигналы, амплитуда которых является случайно величиной, равномерно распределенной в заданном интервале. В число параметров настройки блока входят:
• Minimum — нижняя граница случайных чисел;
• Maximum — верхняя граница;
• Initial seed — начальное значение базы генератора случайных чисел;
• Sample time — дискретизация по времени.
На рисунке 1.22 представлены параметры. Пример процесса, сгенерированного блоком приведен на рис. 1.23.

Рис 1.21
|
|
|
|
Рис 1.22 |
Рис 1.23 |
Блок Band-Limited White Noise
Этот блок (рис1.24) формирует процесс в виде частотно-ограниченного белого шума. Параметры настройки у него следующие:
• Noise power — значение мощности белого шума;
• Sample time — значение дискретности времени (определяет верхнее значение частоты процесса);
• Seed — начальное значение базы генератора случайной величины.
На
рис. 1.26 приведен пример реализации
процесса с помощью
блока Band-Limited
White
Noise
при параметрах, указанных на
рис. 1.25.

Рис 1.24
|
|
|
|
Рис 1.25 |
Рис 1.26 |
-
Структурная схема ЭПС
Электрическая печь сопротивления (ЭПС) представляет собой сложную, многозвенную структуру, звенья которой связаны между собой законами теплообмена. Типовая структурная схема ЭПС, состоящей из нагревателя, стенки (футеровка), изделия и датчика температуры, приведена Передаточные функции элементов печи определяются следующим образом:
1. Нагреватель можно считать теплотехнически тонким телом и его передаточную функцию определить как передаточную функцию инерционного звена первого порядка определяемую зависимостями (2.1):

 (2.1)
(2.1)

где:
 - постоянная времени нагревателя; с
- удельная
теплоёмкость (Дж/м
- постоянная времени нагревателя; с
- удельная
теплоёмкость (Дж/м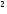 сК);
g
– масса (кг);
F
– площадь поверхности звена (
сК);
g
– масса (кг);
F
– площадь поверхности звена ( );
);
 - коэффициент теплоотдачи (
- коэффициент теплоотдачи ( );
);
 - температура звена в исходном режиме
(К);
- температура звена в исходном режиме
(К);
 - приведённая излучательная способность
(
- приведённая излучательная способность
( ).
).
 на
рис. 2.1
на
рис. 2.1
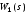 -
передаточная функция нагревателя;
-
передаточная функция нагревателя;
 - то же футеровки;
- то же футеровки;
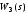 - то же изделия;
- то же изделия;
 - то же датчика; Р
– входное воздействие; к
- то же датчика; Р
– входное воздействие; к - коэффициенты передачи.
- коэффициенты передачи.
2. Футеровку печи можно принять за полуограниченное тело, для которого передаточная функция определяется (3.2):
 (2.2)
(2.2)
где:
 - определяется аналогично
- определяется аналогично
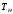 .
.
3. Приняв допущения, что все элементы в камере печи имеют одинаковую температуру во всех режимах, т. е. никакого теплообмена между ними нет, можно определить передаточную функцию печи как (3.3):
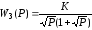
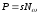 (2.3)
(2.3)
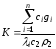
где:
 - нормирующий коэффициент по времени
(ч);
- нормирующий коэффициент по времени
(ч);

 число теплотехнически тонких тел в
рабочем пространстве печи и их суммарная
тепловая ёмкость на 1
число теплотехнически тонких тел в
рабочем пространстве печи и их суммарная
тепловая ёмкость на 1
 поверхности футеровки (
поверхности футеровки ( );
);
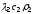 - коэффициент усвоения футеровки (
- коэффициент усвоения футеровки (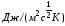 );
);
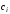 - коэффициент теплопроводности футеровки
(
- коэффициент теплопроводности футеровки
(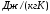 );
);
 - масса теплотехнически тонких тел,
приходящихся на 1
- масса теплотехнически тонких тел,
приходящихся на 1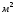 футеровки (
футеровки (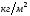 );
);
 - коэффициент теплопроводности футеровки
(
- коэффициент теплопроводности футеровки
( );
);
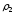 - плотность материала футеровки (
- плотность материала футеровки ( )
)
Коэффициент К характеризует приращение температуры при единичном тепловом потоке за единицу относительного времени.
При многослойной футеровке принимают в расчет лишь теплофизические постоянные ее внутреннего слоя.
4. Передаточная функция датчика температуры (термоэлектрического термометра) при наличии защитного чехла может быть аппроксимирована выражением (3.4):
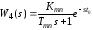 (2.4)
(2.4)
Без защитного чехла датчик практически не обладает запаздыванием и может быть, с достаточной точностью, представлен в виде инерционного звена первого порядка (3.5):
 (2.5)
(2.5)

где:
 - постоянная времени датчика;
- постоянная времени датчика;
 - теплоёмкость, масса, коэффициент
теплопередачи и площадь рабочего конца
термопары.
- теплоёмкость, масса, коэффициент
теплопередачи и площадь рабочего конца
термопары.
Вывод: Изучили основные приёмы моделирования систем автоматического управления в системе MatLAB.
Исследовали системы автоматического регулирования температуры печи сопротивления.