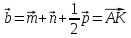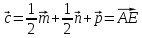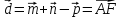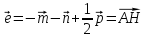Векторы, практическое занятие
..docxВекторы, практическое занятие.
Пример 1.
В
параллелепипеде ABCDA’B’C’D’
заданы векторы, совпадающие с его
ребрами:
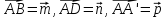 .
.
Построить каждый из следующих векторов:
Получим:

Пример 2.
Проверьте
на коллениарность векторы:
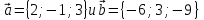
Установить какой из них длиннее и во сколько раз, как они направлены относительно друг друга.
Решение.
Так
как координаты этих векторов
пропорциональны(
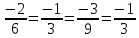 ), то
), то
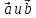 коллениарны.
коллениарны.
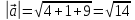
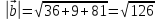
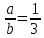 ,
значит вектор
,
значит вектор
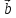 длиннее в 3 раза, чем вектор
длиннее в 3 раза, чем вектор
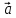 .
.
Так
как отношение всех их координат равно
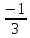 ,
то есть меньше 0, то данные векторы
разнонаправлены.
,
то есть меньше 0, то данные векторы
разнонаправлены.
Пример 3.
Определить
при каких значениях
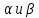 векторы:
векторы:
 коллениарны.
коллениарны.
Решение.
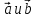 коллениарны
при условии что все их координаты имеют
одинаковые отношения, то есть:
коллениарны
при условии что все их координаты имеют
одинаковые отношения, то есть:
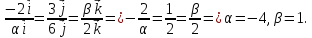
Ответ:
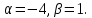
Пример 4.
Доказать что точки: А(3;-1;2), B(1;2;-1), C(-1;1;-3), D(3;-5;3) служат вершинами трапеции.
Решение.
Найдем следующие векторы:
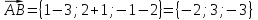
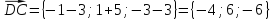
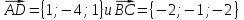
Легко
доказать, что
 коллениарны, а значит AB
и DC
параллельны и что,
коллениарны, а значит AB
и DC
параллельны и что,
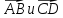 не коллениарны, а значит AB
и СD не параллельны.
не коллениарны, а значит AB
и СD не параллельны.
А так как имеются 4 прямые, две из которых параллельны, а остальные две – нет и пересекают параллельные прямые, то они образуют трапецию, что и требовалось доказать.
Пример 5.
Определить,
при каком значении
 ,
векторы
,
векторы
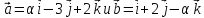 взаимно перпендикулярны.
взаимно перпендикулярны.
Решение.
Скалярное
произведение перпендикулярных векторов
равно 0, верно и обратное, значит, для
того чтобы
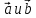 были взаимно перпендикулярны нужно
чтобы их скалярное произведение равнялось
0, получим:
были взаимно перпендикулярны нужно
чтобы их скалярное произведение равнялось
0, получим:


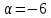
Ответ:

Пример 6.
Даны
векторы
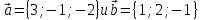 ,
,
Найти координаты векторных произведений:
Решение.
-
2
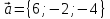
2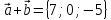
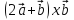 =det
=det
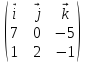 =
=
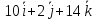 .
.
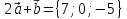
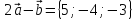
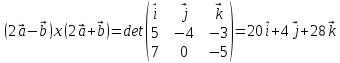
Ответ:
1) =
=
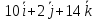 .
.
2)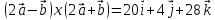 .
.
Пример 7.
Даны вершины треугольника ABC: A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Определите его угол B.
Решение.
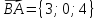 ,
,
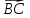 = {7;0;1}
= {7;0;1}
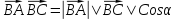 и
в тоже время
и
в тоже время
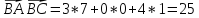
Получим:
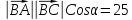 ,
далее найдем
,
далее найдем
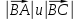 :
:
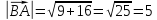 и
и
 .
.
Подставив
полученные данные в выражение
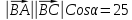 ,
получиим
,
получиим
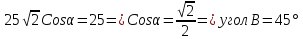 .
.
Ответ:
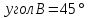 .
.
Пример 8.
Даны
векторы:
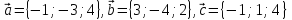 .
Вычислить проекцию вектора
.
Вычислить проекцию вектора
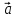 на направление
на направление
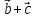 .
.
Решение.
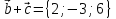 ,
обозначим
,
обозначим
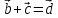 ,
,
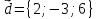 .
.
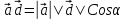 .
.
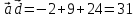 ,
,
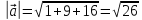 ,
,
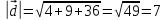 .
.
Подставив полученные данные в исходную формулу, получим:
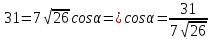 .
.
Проекция
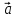 =
=
 =
=
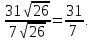
Ответ:
проекция вектора
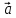 на направление
на направление
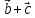 равно
равно
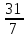 .
.
Задания для самостоятельного решения.
-
Даны вершины четырехугольника: A(1;-2;2), B(1;4;0), C(-4;1;1), D(-5;-5;3). Доказать, что его диагонали взаимно перпендикулярны.
-
Вычислить
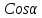 образованный векторами
образованный векторами
 .
. -
Вектор
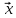 коллениарен
коллениарен
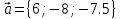 и образует острый угол с осью OZ,
зная, что
и образует острый угол с осью OZ,
зная, что
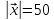 ,
найти его координаты.
,
найти его координаты. -
Найти вектор
 .
. -
Точки A(1;2;0), B(3;0;-3), C(5;2;6) образуют треугольник. Вычислить площадь треугольника ABC.