
Комплексные числа. примеры
.docx
Комплексные числа
Пример 1.
Указать, какие линии определяются этими уравнениями:
а)
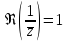 .
.
б)
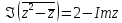 .
.
в)
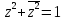 .
.
г)
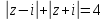 .
.
Решение:
а)
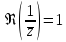 .
.
Пусть
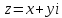 ,
тогда
,
тогда
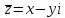 .
.
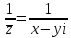 =
=
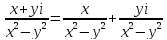 .
.
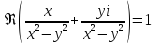 .
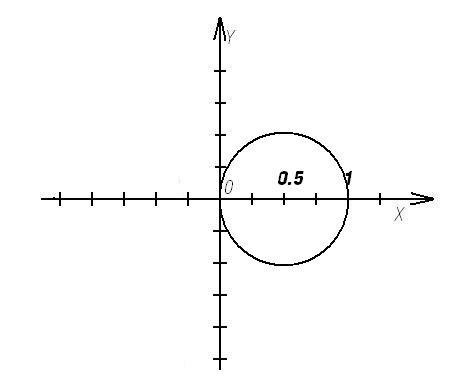
.
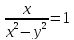 ,
,
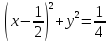 .
.
Ответ:
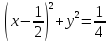 - окружность с центром в точке с
координатами (0,5, 0) и радиусом 0,5.
- окружность с центром в точке с
координатами (0,5, 0) и радиусом 0,5.
б)
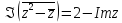 .
.
Пусть
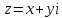 ,
тогда
,
тогда
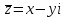 .
.
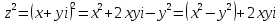 .
.
 .
.
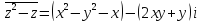 .
.
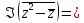
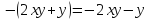 .
.
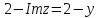 ,
,
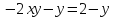 ,
,
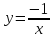 .
.
Ответ:
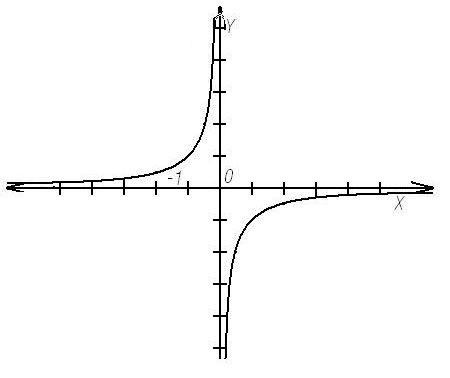
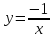 - графиком является гипербола, ветви
которой расположены во второй и четвертой
четверти координатной плоскости.
- графиком является гипербола, ветви
которой расположены во второй и четвертой
четверти координатной плоскости.
в)
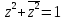 .
.
Пусть
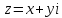 ,
тогда
,
тогда
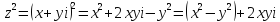 .
.
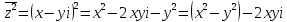 .
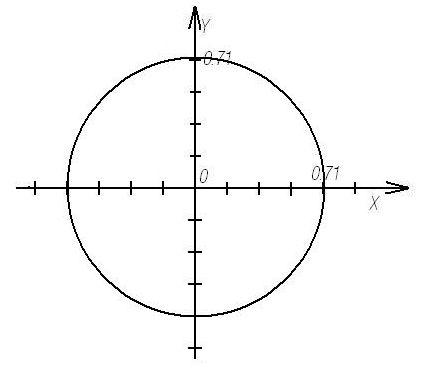
.
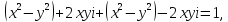
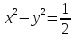 .
.
Ответ:
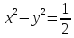 - окружность с центром в начале координат
и радиусом
- окружность с центром в начале координат
и радиусом
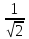 .
.
г)
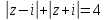 .
.
Пусть
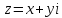 ,
тогда
,
тогда
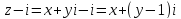 .
.
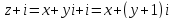 .
.
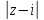 =
=
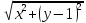 .
.
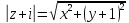 .
.
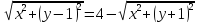 -
возведем полученное уравнение в квадрат
-
возведем полученное уравнение в квадрат
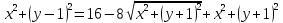 ,
,
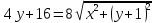 -
возведем ещё раз в квадрат, получим
-
возведем ещё раз в квадрат, получим
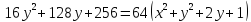 ,
,
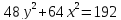 – разделим
обе части уравнения на 192,
– разделим
обе части уравнения на 192,
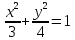 .
.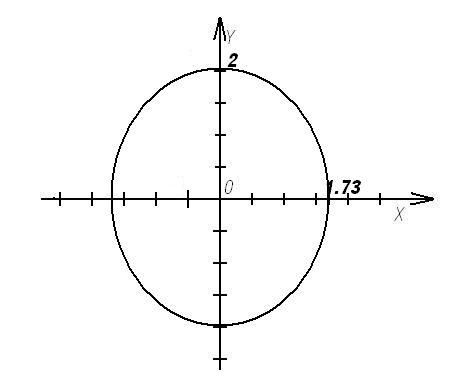
Ответ:
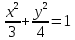 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Пример 2.
Построить множество точек на плоскости комплексной переменной z, которая определяется заданными условиями.
а)
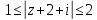 .
.
б)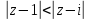 .
.
в)
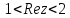 .
.
г)
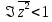 .
.
д)
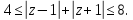
Решение.
а)
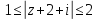 .
.
Пусть
 ,
тогда
,
тогда
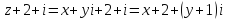 .
.
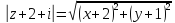 .
.
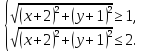 -
Возведем
систему в квадрат, получим
-
Возведем
систему в квадрат, получим
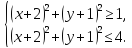
Ответ: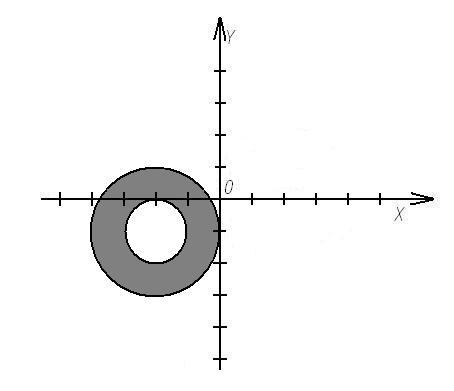
б)
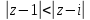 .
.
Пусть
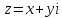 ,
тогда
,
тогда
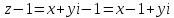 .
.
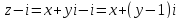 .
.
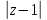 =
=
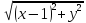 .
.
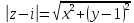 .
.
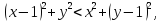
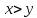 .
.
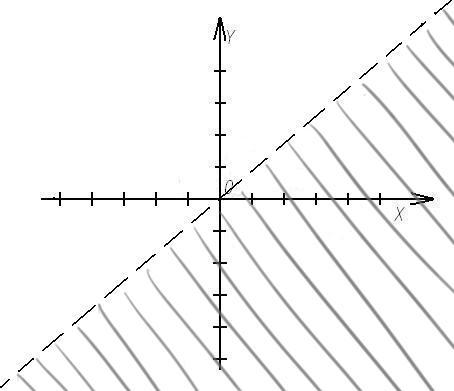
Ответ:
в)
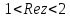 .
.
Пусть
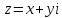 ,
тогда
,
тогда
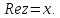
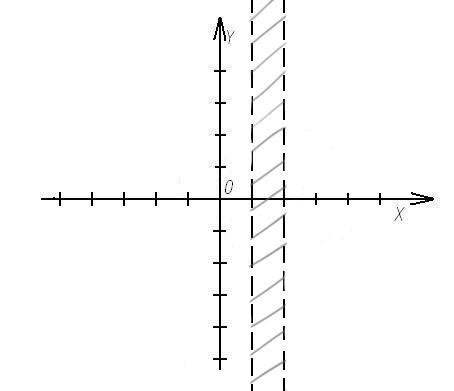
 .
.
Ответ:
г)
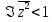 .
.
Пусть
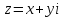 ,
тогда
,
тогда
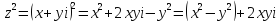 .
.
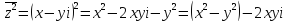 .
.
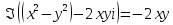 ,
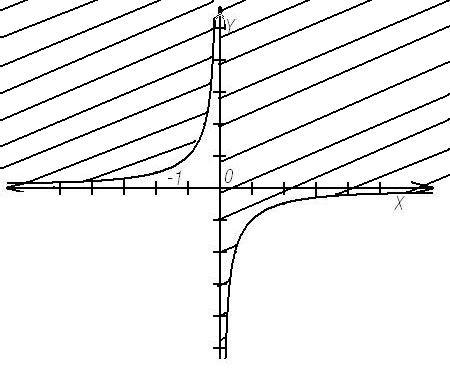
,
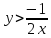 .
.
Ответ:
д)
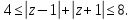
Пусть
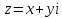 ,
тогда
,
тогда
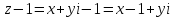 .
.
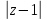 =
=
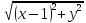 .
.
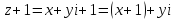 .
.
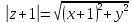 .
.
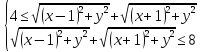 ,
,
Решим первое неравенство системы:
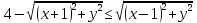 ,
,
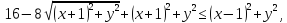
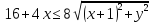 -
возведем обе части неравенства в квадрат.
-
возведем обе части неравенства в квадрат.
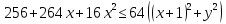 -
раскрываем
скобки, приводим подобные, получаем
-
раскрываем
скобки, приводим подобные, получаем
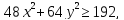
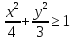 .
.
Решим второе неравенство системы:
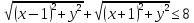 ,
,
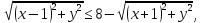 -
возведем обе части неравенства в квадрат,
получим
-
возведем обе части неравенства в квадрат,
получим
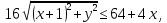 -
ещё раз возведем в квадрат.
-
ещё раз возведем в квадрат.
256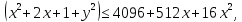
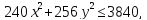
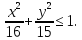
В итоге получаем систему
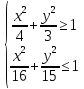

Ответ:
