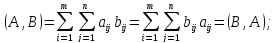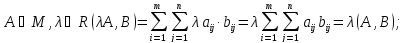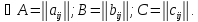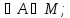Понятие n-мерного евклидова пространства
..docxЛекция №30.
-
Понятие n-мерного евклидова пространства.
Пусть
V
– вещественное или комплексное линейное
пространство. Отображение
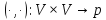 называется скалярным произведением,
если оно удовлетворяет следующим
аксиомам :
называется скалярным произведением,
если оно удовлетворяет следующим
аксиомам :
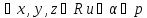 ;
;
-
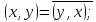
-
(
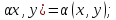
-
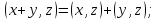
-
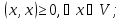
-
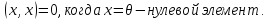
Число
 называют скалярным произведением
называют скалярным произведением
 , (1-5) аксиомы скалярного произведения.
, (1-5) аксиомы скалярного произведения.
Замечание.
В вещественном случае черта первой аксиомы может быть опущена.
Определение.
Вещественное, линейное пространство со скалярным произведением, называют евклидовым пространством, а комплексное – унитарным.
Е – евклидово пространство;
V – унитарное пространство.
Пример.
Доказать,
что векторное пространство М, элементами
которого являются матрицы размеры m
на n
становится евклидовым пространством,
если для
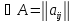 и
и
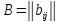 ,
положить
,
положить
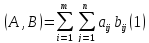 .
.
Достаточно
проверить, что
 определена (1) и удовлетворяет четырём
аксиомам скалярного произведения.
определена (1) и удовлетворяет четырём
аксиомам скалярного произведения.
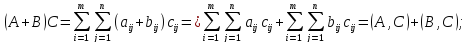
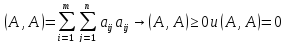 ,
если все элементы
,
если все элементы
 ,
где θ – нулевая матрица.
,
где θ – нулевая матрица.
Выполнены все
аксиомы скалярного произведения, то
есть равенство (1) даёт скалярное
произведение в векторном пространстве евклидово пространство.
евклидово пространство.
Из аксиом следует, что любую конечную линейную комбинацию векторов можно умножить скалярно на другую линейную комбинацию векторов по правилу :
 (2).
(2).
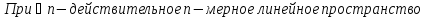 можно многими
способами превратить в евклидово
пространство.
можно многими
способами превратить в евклидово
пространство.
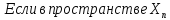 фиксирован базис
фиксирован базис
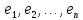 , то
, то
 имеют в нем расположение
имеют в нем расположение
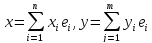 .
.
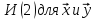 даёт
даёт
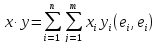 (3).
(3).
Матричная форма.
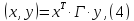 ;
;
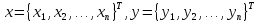 ;
;
 .
.
Матрица
Г- (матрица Грамма) матрица базиса
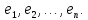
Матрица
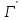 базиса
базиса
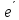 и Г базиса e,
связаны соотношением.
и Г базиса e,
связаны соотношением.
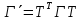 ,
(5) где Т –
матрица перехода от е к е΄.
,
(5) где Т –
матрица перехода от е к е΄.
Длина
 в линейном пространстве
в линейном пространстве

 , (6).
, (6).
Нормировать
ненулевой вектор, значит, заменить его
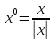 , (7).
, (7).
Углом
между ненулевыми векторами
 Еn
называется угол β определяемый
соотношением :
Еn
называется угол β определяемый
соотношением :
 ,
,
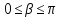 ,
(8).
,
(8).
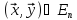 называются
ортогональными, если
называются
ортогональными, если
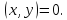
Система векторов называется ортогональной, если в ней все векторы попарно ортогональны.
Система вектором называется ортонормированной, если она ортогональна и в ней все векторы нормированы.
Базис
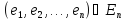 называется ортогональным базисом, если
его векторы попарно ортогональны. Если
кроме того, векторы этого базиса имеют
одинаковую длину, то он называется
ортонормированным.
называется ортогональным базисом, если
его векторы попарно ортогональны. Если
кроме того, векторы этого базиса имеют
одинаковую длину, то он называется
ортонормированным.
-
Ортогонализация Грамма – Шмидта.
От
любой линейно независимой системы
векторов
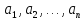 евклидова пространства можно перейти
к ортогональной системе ненулевых
векторов
евклидова пространства можно перейти
к ортогональной системе ненулевых
векторов
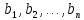 состоящей так же из n
векторов. Такой переход осуществляется
с помощью процесса ортогонализации
Грамма- Шмидта.
состоящей так же из n
векторов. Такой переход осуществляется
с помощью процесса ортогонализации
Грамма- Шмидта.
Положим,
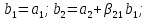

Найдём
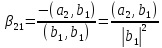 .
.
 .
.
Следовательно,
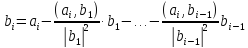 ,
(9).
,
(9).
-
Изоморфизм линейных пространств.
Два линейных пространства V и U называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, выполняемое условием :
Сумме векторов линейного пространства U соответствует сумма соответствующих векторов линейного пространства V.
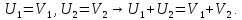
Произведение числа на вектор линейного пространства U соответственно равен произведению того же числа на соответствующий вектор V.
Изоморфизм – это взаимно однозначное соответствие сохранения линейной операции.
Изоморфизм евклидовых пространств.
Линейные
евклидова пространства
 называют изоморфными, если между их
векторами можно установить такое взаимно
однозначное соответствие, такое, что
выполняется следующее требование:
называют изоморфными, если между их
векторами можно установить такое взаимно
однозначное соответствие, такое, что
выполняется следующее требование:
1)Это
соответствие является изоморфным
соответствием между
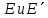 ,
которые в свою очередь рассматриваются
как линейные пространства.
,
которые в свою очередь рассматриваются
как линейные пространства.
2)
При этом соответствии сохраняется
скалярное произведение, то есть, если
образами
 из Е служат соответственно
из Е служат соответственно
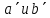 из Е΄, то
из Е΄, то
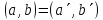 ,
(10).
,
(10).
Теорема.
Любые Е и Е΄ имеющие одну и ту же размерность n – изоморфны между собой.
Доказательство:
Выберем в пространствах Е и Е' ортонормированные базы
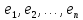 (11) и соответственно
(11) и соответственно
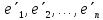 (12).
(12).
Ставя
в соответствие всякому вектору
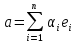 ,
из Е вектор
,
из Е вектор
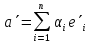 ,из Е΄ имеющий в базисе те же координаты,
что и вектор
,из Е΄ имеющий в базисе те же координаты,
что и вектор
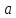 в своём базисе, мы получим очевидное
изоморфное соответствие между линейными
пространствами Е и Е΄ . Покажем что
выполняется равенство (10), если :
в своём базисе, мы получим очевидное
изоморфное соответствие между линейными
пространствами Е и Е΄ . Покажем что
выполняется равенство (10), если :
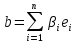 ,
,
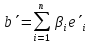 .
.
И учитывая ортонормированность баз (11) и (12), получим:
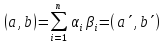 .
.
Естественно изоморфные евклидовы пространства не считаются различными. Поэтому для всякого n существует единое n-мерное евклидово пространство в том же смысле, в каком для всякого n существует единственное n-мерное действительное линейное пространство.