Понятие линейного оператора

Лекция 28

Понятие линейного оператора

Определение 1. Рассмотрим два линейных пространства R и R₁ над полем K. Оператором ã называется любое правило, согласно которому каждому вектору ставится в соответствие единственный вектор , такой, что . Вектор называется образом вектора , а вектор 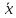- прообразом вектора .

Определение 2. Оператор ã называется линейным, если выполняются следующие 2 условия:

a) ;

b) .

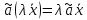Матрица линейного оператора в заданном базисе

Пусть и – линейные пространства размерности n и m соответственно. Пусть A – линейный оператор, действующий из L₁ в L₂. Зафиксируем в пространстве L₁ базис . Рассмотрим действие линейного оператора A на векторы базиса Разложим векторы по базису :

Коэффициенты этих разложений образуют матрицу , которая называется матрицей линейного oператора A в паре базисов e и f.

Основные действия над линейными операторами

Пусть L₁ и L₂ – произвольные линейные пространства.

Определение. Операторы и называются равными, если .

Определение. Суммой операторов и называется оператор , действующий по правилу

Определение. Произведением оператора на действительное число λ называется оператор , действующий по правилу .

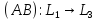Определение. Произведением операторов и называется оператор , действующий по правилу

Определение. Пусть . Определим степень оператора A следующим образом: , где единичный оператор, действующий по правилу .

Легко доказать следующие утверждения.

Утверждение 1. Если A и B – линейные операторы, то также линейные операторы (при условии, что существуют).

Утверждение 2. В конечномерных линейных пространствах произведению линейного оператора на число, сумме линейных операторов и произведению линейных операторов соответствуют такие же действия с их матрицами.

Понятие собственного вектора и собственного значения линейного оператора. Характеристическая матрица и характеристический многочлен матрицы. Подобные матрицы, их характеристические многочлены

Пусть выражается линейно через :

,

тогда с координатами переводятся в вектор 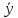с помощью линейного преобразования (1) с матрицей А.

Пусть имеется линейное преобразование (оператор) с матрицей А, если существует , такая, что (2), то λ называется собственным числом (значением), а 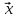- собственным вектором линейного преобразования соответствующего числа λ.

Из (2) следует 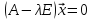, где E – единичная матрица.

Матричное уравнение соответствует следующей системе уравнений:

Чтобы эта система имела ненулевое решение, необходимо, чтобы ее определитель был равен 0, поэтому собственные значения являются корнями уравнения , то есть

(5) называется характеристическим уравнением.

Чтобы найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей А, поступает следующим образом:

1. составляют характеристическое уравнение (5);

2. находим корни λ характеристического уравнения;

3. каждое подставляется в систему (4). Находим все ее линейно-независимые решения, которые будут определять собственный вектор, соответствующий данному . Для каждого существует бесконечно много коллинеарных соответствующих векторов.

Определение. Характеристическим многочленом относительно числа λ называется многочлен вида .

Характеристические многочлены подобных матриц совпадают.

Характеристический многочлен и характеристические корни линейного оператора

Определение. Уравнение называется характеристическим уравнением оператора A.

Теорема. Для того чтобы число λ являлось собственным значением

оператора A, необходимо и достаточно, чтобы оно было действительным корнем характеристического уравнения оператора A.

Теорема о линейной независимости собственных векторов, отвечающих различным собственным значениям линейного оператора.

Теорема. Пусть собственные значения линейного оператора A попарно различны. Тогда система соответствующих им собственных векторов линейно независима.

Доказательство.

Доказательство опирается на метод математической индукции, проводимый по количеству n векторов в системе. При n = 1 утверждение теоремы верно, так как линейная независимость системы из одного вектора означает, что этот вектор ненулевой, а собственный вектор, согласно определении., является ненулевым.

Пусть утверждение верно при n = m, то есть для произвольной системы из m собственных векторов . Добавим к системе векторов еще один собственный вектор , отвечающий собственному значению , и докажем, что расширенная таким способом система векторов останется линейно независимой. Рассмотрим произвольную линейную комбинацию полученной системы собственных векторов и предположим, что она равна нулевому вектору:

К равенству (1) применим линейный оператор A и в результате получим еще одно векторное равенство

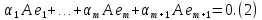
Учтем, что векторы являются собственными:

Вспоминая, что система векторов , по предположению, линейно независима, делаем вывод, что у полученной линейной комбинации все коэффициенты равны нулю:

Поскольку все собственные значения λi попарно различны, то из равенств (3) следует, что . Значит соотношение (1) можно записать в виде , а так как вектор ненулевой (как собственный вектор), то . В итоге получаем, что равенство (1) выполняется лишь в случае, когда все коэффициенты , равны нулю. Тем самым мы доказали, что система векторов линейно независима.

Теорема о существовании базиса, состоящего из собственных векторов линейного оператора

Теорема 1. Матрица линейного оператора A, действующего в линейном пространстве, в данном базисе является диагональной тогда и только тогда, когда все векторы этого базиса являются собственными для оператора A.

Доказательство:

Пусть A — матрица линейного оператора A в базисе . Согласно определению, j-м столбцом матрицы A является столбец координат вектора Ab_j.

Если матрица A является диагональной, то произвольно взятый ее j-й столбец имеет вид (0 . . . 0 µ_j 0 . . . 0)^т (единственный ненулевой элемент стоит на j-м месте). Для вектора Ab_j получаем представление Ab_j = b(0 . . . 0 µ_j 0 . . . 0)^т= µ_jb_j, которое как раз и означает, что вектор b_j является собственным с собственным значением µ_j. Значит, все базисные векторы являются собственными, а все диагональные элементы матрицы A являются собственными значениями.

Верно и обратное. Если каждый вектор b_j является собственным для линейного оператора A и ему отвечает собственное значение λ_j, то Ab_j = λ_jb_j = b(0 . . . 0 λ_j 0 . . . 0)^т, т.е. в матрице оператора A в этом базисе равны нулю все элементы, кроме диагональных, а диагональный элемент в j-м столбце равен λ_j.

Следствие 1. Если характеристическое уравнение линейного оператора, действующего в n-мерном линейном пространстве, имеет n попарно различных действительных корней, то существует базис, в котором матрица этого оператора является диагональной.

Доказательство:

Каждый действительный корень характеристического уравнения является собственным значением линейного оператора. Каждому из таких корней можно сопоставить хотя бы по одномусобственному вектору. Система выбранных таким образом векторов, согласно теореме о линейной независимости собственных векторов, является линейно независимой, а так как количество n векторов в ней равно размерности линейного пространства, она является базисом. Этот базис состоит из собственных векторов.

Согласно теореме 1, матрица линейного оператора в этом базисе имеет диагональный вид.

Следствие 2. Если характеристическое уравнение квадратной матрицы порядка n имеет n попарно различных действительных корней, то эта матрица подобна некоторой диагональной.

Доказательство:

Пусть характеристическое уравнение матрицы A порядка n имеет n различных действительных корней. Выберем произвольное n-мерное линейное пространство L, зафиксируем в нем некоторый базис b = (b₁, b₂, . . . , b_n) и рассмотрим линейный оператор A, матрицей которого в базисе b является матрица A. По теореме 1 существует базис, в котором матрица A'

этого оператора диагональна. Матрицы A и A' подобны. Отметим, что

на диагонали матрицы A' стоят все попарно различные собственные значения матрицы A.