
Фундаментальная система решений
Рассмотрим систему однородных линейных алгебраических уравнений.
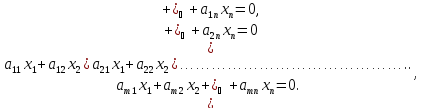 (1)
(1)
Выпишем матрицу A

Определение 1.
Минор матрицы называется базисным , если он неравен 0, и окаймляющие его миноры либо все равны 0, либо совсем отсутствуют.
Теорема о базисном миноре.
Столбцы матрицы, пересекающие главный минор линейно независимы; Всякий столбец через них линейно выражается.
Определение 2.
Всякая максимальная линейно независимая система решений однородной системы уравнений (1), называется фундаментальной системой решений (ФСР).
Теорема:
Если ранг r , матрицы из коэффициентов системы линейных однородных уравнений (1), меньше m, то всякая ФСР системы (1) состоит из n-r решений.
Пример №1.
Дана однородная система линейных алгебраических уравнений
 .
.
Найти ФСР и общее решение системы.
1.Составим матрицу системы.
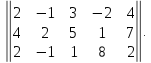
2. Легко показать, что ранг матрицы A=2, значит ФСР состоит из трех решений (5-2=3).
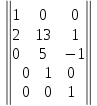
3. В матрице A возьмем базисный минор (минор второго порядка):
 .
.
4.
Отбрасываем последние уравнения системы
, а неизвестные
 ,
,
считаем «свободными» и переносим их в правую часть уравнений.
Получим:
 .
(2)
.
(2)
5.
Ищем первое базисное решение X
, для этого положим
 ,
тогда получим систему:
,
тогда получим систему:
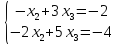 (3)
(3)
Определителем
матрицы системы является базисный
минор, он отличен от 0, значит система
(3) имеет единственное решение:
 .
.
Таким образом
 =
=
 .
.
6.
Полагая в системе (2) ,
находим
,
находим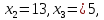 то
есть, вторым базисным решением является
столбец:
то
есть, вторым базисным решением является
столбец:
 .
.
7.
Полагая:
 ,
получаем -
,
получаем -
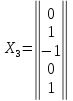 .
.
8. Итак, ФСР получена; построенная таким образом ФСР называется нормальной.
9.
Столбцы
 образующие ФСР линейно независимы, так
как свободные неизвестные были выброшены
так, что выделенный минор третьего
порядка отличен от 0;
образующие ФСР линейно независимы, так
как свободные неизвестные были выброшены
так, что выделенный минор третьего
порядка отличен от 0;
10.Теперь выпишем общее решение исходной однородной системы линейных алгебраических уравнений.
 ,
,
 .
.
Неоднородная система линейных алгебраических уравнений
 (1)
(1)
Общее решение неоднородной системы линейных алгебраических уравнений (1) имеет вид:
 (2)
(2)
где
 – какое-либо решение системы (1).
– какое-либо решение системы (1).
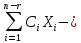
общее
решение соответствующей однородной
системы, для которой
 – ФСР.
– ФСР.
Пример №2.
Дана неоднородная система линейных алгебраических уравнений:

Доказать, что это система совместна и найти ее общее решение.
Решение:
Легко показать, что rang Ᾱ = rang A
Рассмотрим соответствующую однородную систему уравнений, эта система из примера №1. Её ФСР и общее решение найдены. Выделим в матрицу Ᾱ базисный минор, стоящий на пересечении первых двух строк со вторым и третьим столбцами. Тогда последовательность уравнений системы есть следствие двух первых уравнений системы, а неизвестные
 можно считать «свободными», поэтому
исходная система эквивалентна системе:
можно считать «свободными», поэтому
исходная система эквивалентна системе:



Решив
её, находим единственное решение:

Найдено частное решение данной неоднородной системы.
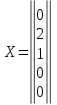 .
.
Общее решение исходной неоднородной системы получим с помощью формулы (2).
 =
=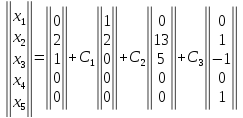 или
или

Это
решение можно было бы получить методом
исключения неизвестных. ФСР определяется
неоднозначно,
но число элементов в ФСР всегда равно
 .
.
