
Задания на первый семестр
.doc
Задания для студентов-сокращёнников заочного отделения 1 курса 2012-2013 г.г. (группы сзУПТС-11, сзУПТС-12) по предмету: „Программирование и основы алгоритмизации“
Студент выполняет задания, номера которых указаны напротив его ФИО в приведенной ниже таблице. Тексты задач приведены ниже.
|
№ |
ФИО |
№№ заданий |
|
1 |
Бейбулатова Светлана Ивановна |
1, 38, 75, 3, 45, 82 |
|
2 |
Бойко Алексей Михайлович |
2, 39, 76, 4, 46, 83 |
|
3 |
Будеркин Дмитрий Сергеевич |
3, 40, 77, 5, 47, 84 |
|
4 |
Васильев Роман Константинович |
4, 41, 78, 6, 48, 85 |
|
5 |
Веткасов Дмитрий Юрьевич |
5, 42, 79, 7, 49, 86 |
|
6 |
Гладкий Алексей Алексеевич |
6, 43, 80, 8, 50, 87 |
|
7 |
Говорухин Андрей Михайлович |
7, 44, 81, 9, 51, 88 |
|
8 |
Долматов Андрей Андреевич |
8, 45, 82, 10, 52, 89 |
|
9 |
Захаров Алексей Юрьевич |
9, 46, 83, 11, 53, 90 |
|
10 |
Зверев Александр Викторович |
10, 47, 84, 12, 54, 91 |
|
11 |
Корешков Александр Викторович |
11, 48, 85, 13, 55, 92 |
|
12 |
Коршунова Маргарита Сергеевна |
12, 49, 86, 14, 56, 93 |
|
13 |
Красноштан Владимир Александрович |
13, 50, 87, 15, 57, 94 |
|
14 |
Кристофович Никита Валерьевич |
14, 51, 89, 16, 58, 95 |
|
15 |
Куприянов Николай Николаевич |
15, 52, 90, 17, 59, 96 |
|
16 |
Ларин Дмитрий Сергеевич |
16, 53, 91, 18, 60, 97 |
|
17 |
Маврин Александр Романович |
17, 54, 92, 19, 61, 98 |
|
18 |
Махова Юлия Сергеевна |
18, 55, 93, 20, 62, 99 |
|
19 |
Мельников Никита Андреевич |
19, 56, 94, 21, 63, 100 |
|
20 |
Мельников Сергей Олегович |
20, 57, 95, 22, 64, 101 |
|
21 |
Мещеряков Валерий Алексеевич |
21, 58, 96, 23, 65, 102 |
|
22 |
Михайлов Иван Алексеевич |
22, 59, 97, 24, 66, 103 |
|
23 |
Муслумов Валерий Русланович |
23, 60, 98, 25, 67, 104 |
|
24 |
Наумов Анатолий Анатольевич |
24, 61, 99, 26, 68, 105 |
|
25 |
Погребнов Виталий Сергеевич |
25, 62, 100, 27, 69, 106 |
|
26 |
Проскурняк Сергей Михайлович |
26, 63, 101, 28, 70, 107 |
|
27 |
Солейник Егор Алексеевич |
27, 64, 102, 29, 71, 108 |
|
28 |
Томилко Павел Николаевич |
28, 65, 103, 30, 72, 109 |
|
29 |
Фадейкин Сергей Дмитриевич |
29, 66, 104, 31, 73, 110 |
|
30 |
Филиппенко Кирилл Олегович |
30, 67, 105, 32, 74, 20 |
|
31 |
Чеканов Евгений Васильевич |
31, 68, 106, 33, 75, 21 |
|
32 |
Чекменев Альберт Анатольевич |
32, 69, 107, 34, 76, 22 |
|
33 |
Ширяева Ольга Александровна |
33, 70, 108, 35, 77, 23 |
|
34 |
Шулятьева Ирина Сергеевна |
34, 71, 109, 36, 78, 24 |
|
35 |
|
35, 72, 110, 37, 79, 25 |
|
36 |
|
36, 73, 1, 38, 80, 26 |
|
37 |
|
37, 74, 2, 39, 81, 27 |
|
38 |
|
38, 75, 3, 40, 82, 28 |
|
39 |
|
39, 76, 4, 41, 83, 29 |
|
40 |
|
40, 77, 5, 42, 84, 30 |
|
41 |
|
41, 78, 6, 43, 85, 31 |
|
42 |
|
42, 79, 7, 44, 86, 32 |
|
43 |
|
43, 80, 8, 45, 87, 33 |
|
44 |
|
44, 81, 9, 46, 88, 34 |
|
45 |
|
45, 82, 10, 47, 89, 35 |
|
46 |
|
46, 83, 11, 48, 90, 36 |
|
47 |
|
47, 84, 12, 49, 91, 37 |
|
48 |
|
48, 85, 13, 50, 92, 38 |
|
49 |
|
49, 86, 14, 51, 93, 39 |
|
50 |
|
50, 87, 15, 52, 94, 40 |
|
51 |
|
51, 88, 16, 53, 95, 41 |
|
52 |
|
52, 89, 17, 54, 96, 42 |
|
53 |
|
53, 90, 18, 55, 97, 43 |
|
54 |
|
54, 91, 19, 56, 98, 44 |
|
55 |
|
55, 92, 20, 57, 99, 45 |
|
56 |
|
56, 93, 21, 58, 100, 46 |
|
57 |
|
57, 94, 22, 59, 101, 47 |
|
58 |
|
58, 95, 23, 60, 102, 48 |
|
59 |
|
59, 96, 24, 61, 103, 49 |
|
60 |
|
60, 97, 25, 62, 104, 50 |
|
61 |
|
61, 98, 26, 63, 105, 51 |
|
62 |
|
62, 99, 27, 64, 106, 52 |
|
63 |
|
63, 100, 28, 65, 107, 53 |
|
64 |
|
64, 101, 29, 66, 108, 54 |
|
65 |
|
65, 102, 30, 67, 109, 55 |
|
|
|
|
|
|
|
|
|
|
|
|
-
Напечатать все простые числа, не превосходящие заданное число М.
-
Задан массив А(М) из М из попарно различных чисел. Напечатать все перестановки этих чисел.
-
Ввести вещественное число А и натуральное k. Вычислить и напечатать Ak с выполнением следующих условий: операцией возведения в степень пользоваться нельзя; k может оказаться настолько большим, что недопустимо выполнять k умножений.
-
В написанном выражении ((((1?2)?3)?4)?5)?6 вместо знака ? вставить знак одной из четырех арифметических операций + – * /, так чтобы результат вычислений равнялся 35 (при делении дробная часть в частном отбрасывается). Достаточно найти одно решение.
-
Дан двухмерный целочисленный массив А(2,N). Известно, что среди его элементов два и только два равны между собой. Напечатать их индексы.
-
Можно ли заданное натуральное число М представить в виде суммы двух квадратов натуральных чисел? Написать программу решения этой задачи.
-
Даны натуральное число М и целочисленный массив А(М). Сосчитать и напечатать, сколько различных чисел в этом массиве. Например, в массиве 5,7,5 различных чисел два (5 и 7).
-
Составить программу вывода всех трехзначных десятичных чисел, сумма цифр которых равна данному целому числу.
-
Целое неотрицательное число М задано массивом своих двоичных цифр a0, a1, a2, … an-1:
M= an-1 2n-1 + an-1 2n-2+…+ a1 2+a0
где ai=0 или ai=1 (i=0, …, n-1). Напечатать массив двоичных цифр числа М+1.
-
В массиве X(M,N) все числа различны. В каждой строке выбирается минимальный элемент, затем среди всех этих чисел выбрать максимальное. Напечатать номер строки массива Х, в котором расположено это число.
-
В массиве Х(N) каждый элемент равен 0,1 или 2. Переставить элементы массива так, чтобы располагались все нули, затем все единицы и, наконец, все двойки (дополнительного массива не заводить).
-
Функция f (n) для целых неотрицательных n определена:
f (0)=0, f (1)=1, f (2n)= f (n), f (2n+1)= f (n)+ f (n)
Для данного найти и напечатать f (N). Обязательное условие: N столь велико, что недопустимо заводить массив из N чисел (равно как и массив, длина которого растет с ростом N)
-
Найти минимальное число, которое представляется суммой четырех натуральных чисел не единственным образом.
-
Вывести число n и заполнить массив размером nn натуральными числами от 1 до n2 по спирали.
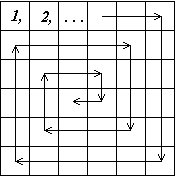
-
-
Напечатать все четырехзначные натуральные числа, в десятичной записи нет двух одинаковых цифр. Обобщить данную задачу для n мерного числа.
-
Заданы число N и целочисленный массив A(N). Найти длину самой длинной последовательности подряд идущих элементов массива, равных нулю.
-
На квадратном клетчатом листе бумаги (размера 100100 клеток) нарисовано несколько прямоугольников. Каждый прямоугольник состоит из целых клеток, различные прямоугольники не накладываются друг на друга и не соприкасаются (см. рисунок). Задан массив 100100, в котором aij=1, если клетка (i,j) принадлежит какому либо прямоугольнику, и aij=0 в противном случае. Написать программу, которая сосчитает и напечатает число прямоугольников.

-
-
Напечатать в порядке возрастания все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7.
-
Даны целочисленный массив A(N) и число M. Найти такое множество A(i1), A(i2), … A(ik), (1 i1 i2 ik N), что A(i1) + A(i2) + … + A(ik)=M. Предполагается, что такое множество заведомо существует.
-
Дан одномерный массив. Все его элементы, не равные нулю, переписать (сохраняя их порядок) в начало массива, а нулевые элементы – в конец массива (новый массив не заводить).
-
Даны числа M,N и двухмерный массив размером MN. Некоторый элемент этого массива назовем седловой точкой, если он является наименьшим в своей строке и наибольшим в столбце. Напечатать номера строки и столбца какой-нибудь седловой точки и напечатать число 0, если такой точки нет.
-
Даны числа N,K и два целочисленных массива X(N) и Y(K). Можно ли в первом из них выбрать такие K идущих подряд элементов Xi+1, Xi+2, … Xi+k, чтобы Xi+1=Y1, Xi+2=Y2, … Xi+k=Yk,? Написать программу, которая решает данную задачу и и печатает ответ ДА или НЕТ.
-
Бит-реверс. Целое положительное число M записывается в двоичной системе счисления и разряды (в это записи) переставляются в обратном порядке. Получившееся число принимается за значение функции B(M). Напечатать значения B(M) для M =512, 513, 514, … , 1023. Вот, для ясности, начало этой распечатки: 1, 513, 257, … ,1023.
-
Треугольник и точка. Заданы прямоугольные координаты x1, y1, x2, y2, x3, y3 вершин треугольника и координаты x, y точки. Определить и напечатать, находится ли точка в треугольнике. Погрешностями вычислений пренебречь.
-
Лабиринт. Может ли путник выйти из лабиринта? Если может, то напечатать путь от выхода до начального положения путника. Лабиринт задан массивом А размером 4040 в котором: Акм=0 если клетка (К, М) «проходима»; Акм=1 если клетка (К, М) «не проходима». Начальное положение путника задается в проходимой клетке (I, J). Путник может перемещаться из одной клетки в другую, если они имеют общую сторону. Путник выходит из лабиринта, когда попадает в граничную клетку (то есть (К, М), где К или М равны 1 или 40).
-
Пила. Задан массив X(N). Найти длину К самой длинной «Пилообразной (зубьями вверх)» последовательности идущих подряд чисел: Хр+1< Хр+2> Хр+3< …> Хр+k.
-
Сократить дробь. Даны натуральные числа M и N. Найти такие натуральные числа M1 и N1, не имеющие общего делителя, что M1/N1=M/N.
-
Инверсия. Пусть P=(p1, …pn) является перестановкой чисел 1, 2, … , n. Таблицей инверсии перестановки Р называют последовательность T= (t1, … , tn), в которой ti равно числу элементов перестановки Р, стоящих (в Р) левее числа i и больше числа i. Например, для перестановки Р=(5, 9, 1, 8, 2, 6, 4, 7, 3) чисел (1, 2, … , 9) таблица инверсии Т= (2, 3, 6, 4, 0, 2, 2, 1, 0). Написать программу, которая по заданной таблице инверсий восстанавливает перестановку.
-
Дорога. Даны натуральные числа N 2 и M и вещественный массив A(M,M,N-1). Найти минимальное значение суммы R=A(,1) + A(i2,i3,2) + … +A(iN-1,iN,N-1) для всевозможных наборов чисел 1 i1, i2, … , iN М.
Пояснение. Числа M, N – величины порядка несколько десятков. Поэтому неприемлемо решение с числом действий порядка MN.
-
Совершенные числа. Натуральное число называется совершенным, если оно равно сумме всех своих собственных делителей, включая 1. Напечатать все совершенные числа, меньшие заданного М.
-
Период дроби. Введите натуральные числа M и N и напечатать период десятичной дроби M/N. Например, для дроби 1/7 период будет (142857), а если дробь конечная, то ее период состоит из одной цифры 0.
-
Слияние массивов. Даны два числа M, N и два упорядоченных массива a1 a2 … aM и b1 b2 … bN . Образовать из этих элементов упорядоченный массив с1 с2 … сM+N.
-
Календарь. Заданны три числа А, В, С которые обозначают число, месяц и год. Найти номер N указанного дня с начала года.
Указание: високосные годы – это те, у которых номер делится на 400, и, те, у которых номер делится на 4, но не делится на 100.
-
Квадратики. Дан массив A(M,N), каждый элемент которого равен 0, 1, 5 или 11. Подсчитать в нем количество четверок A(i,j), A(i+1,j), A(i, j+1), A(i+1,j+1), в каждой из которых все элементы различны.
-
Написать программу нахождения самой тяжёлой и самой легкой из 100 монет различной массы, если можно сделать не более 150 взвешиваний на чашечных весах без гирь. Какое минимальное число взвешиваний надо сделать, чтобы гарантированно определить искомые монеты?
-
Составить программу, проверяющую, является ли данное число n простым. Если введённое число не простое, то должен быть возвращён его делитель.
-
Составить программу, выдающую все целые делители натурального числа n.
-
На числовой оси живёт Кузнечик, который умеет прыгать на 1 и на 4 вправо и влево. В точках с координатами 0, 4, 8, 12 и т.д. ему находится нельзя, потому что в них он будет съеден лягушками. Составить программу, которая находила бы способ, как Кузнечику попасть из точки с координатой a в точку с координатой b ровно за N прыжков. Если это сделать невозможно, должно быть выведено соответствующее сообщение.
-
Число, равное сумме всех его делителей (без самого числа), называется совершенным. Например, числа 6=1+2+3; 28=1+2+4+7+14 – совершенные числа. Составить программу поиска всех совершенных чисел среди натуральных от 1 до N (N =2109).
-
Христиан Гольдбах высказал предположение, что любое нечетное число, большее 5, можно представить в виде суммы трех простых чисел. Составить программу, проверяющую это предположение для произвольного нечетного числа от 0 до 200000.
-
Пара чисел, каждое из которых равно сумме делителей другого числа (не считая самого числа), называются дружественными. Например, числа 220 и 284 – дружественные. Леонард Эйлер нашел в XVIII в. 65 пар дружественных чисел. Составить программу поиска дружественных чисел в диапазоне от 0 до 2000000.
-
Даны натуральные числа M и N. Написать программу, которая найдет наименьшие натуральные числа m и n, что m/n=M/N.
-
Среди 2n+1 различных по массе монет нужно найти среднюю (которая тяжелее n монет и легче оставшихся n монет). Напишите программу, которая сделает это не более чем за 100n взвешиваний на чашечных весах без гирь.
-
Заданы два массива чисел длины n и m (n>m) соответственно. Составить программу, определяющую, можно ли вычеркнуть некоторые элементы из большего массива, чтобы получить меньший. (Порядок элементов в массивах роли не играет).
-
Заданы два массива чисел длины n и m (n>m) соответственно. Составить программу, определяющую максимальное число k такое, что путём вычеркивания некоторых элементов из данных массивов можно получить два одинаковых массива длины k. (Порядок элементов в массивах роли не играет).
-
Задачу про ханойские башни по преданию придумали буддийские монахи. Они занимались перекладыванием 64 колец. Согласно легенде, в момент, когда они кончат складывать кольца, наступит конец света. Считая, что на перекладывание одного кольца необходимо 1 секунду, оценить, когда наступит конец света.
-
Составить программу нахождения первых n простых чисел.
-
Составить программу, проверяющую предположение: «Любое четное число, большее 2, можно представить в виде суммы двух простых чисел» для чисел от 0 до 200000.
-
Составить программу, выдающую все четные числа от 4 до 200000, которые нельзя представить в виде суммы двух простых чисел.
-
Задана целочисленная прямоугольная матрица. Составить программу, получающую новую матрицу следующим образом: в каждом столбце исходной матрицы элементы заменяются суммой элементов из строк, расположенных ниже (последняя строка должна стать нулевой). Размер матрицы большой и заводить вспомогательную матрицу такого же размера не представляется возможным.
-
Задана целочисленная прямоугольная матрица. Составить программу, получающую новую матрицу следующим образом: в каждой строке исходной матрицы элементы заменяются суммой элементов из предыдущих столбцов (первый столбец должен стать нулевым). Размер матрицы большой и заводить вспомогательную матрицу такого же размера не представляется возможным.
-
Написать программу, получающую из заданной последовательности чисел длины N все числа, которые входят в нее по одному разу.
-
Два простых числа, разность которых равна 2, называют близнецами. Составить программу поиска чисел-близнецов от 5 до 200000.
-
Элемент последовательности называется локальным максимумом, если у него нет соседа, большего, чем он сам. Аналогично элемент последовательности называется локальным минимумом, если у него нет соседа, меньшего, чем он сам. Составить программу, подсчитывающую число локальных максимумов и локальных минимумов и последовательности длины n.
-
Элемент последовательности называется локальным максимумом, если у него нет соседа, большего, чем он сам. Аналогично элемент последовательности называется локальным минимумом, если у него нет соседа, меньшего, чем он сам. Составить программу, подсчитывающую число локальных максимумов и локальных минимумов и последовательности длины n.
-
Напишите программу порождения всех перестановок целых чисел от 1 до n.
-
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для
любого заданного a.
для
любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы

-
Напишите оптимальную по быстродействию программу для вычисления значения суммы

-
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы

-
Напишите оптимальную по быстродействию программу для вычисления значения суммы
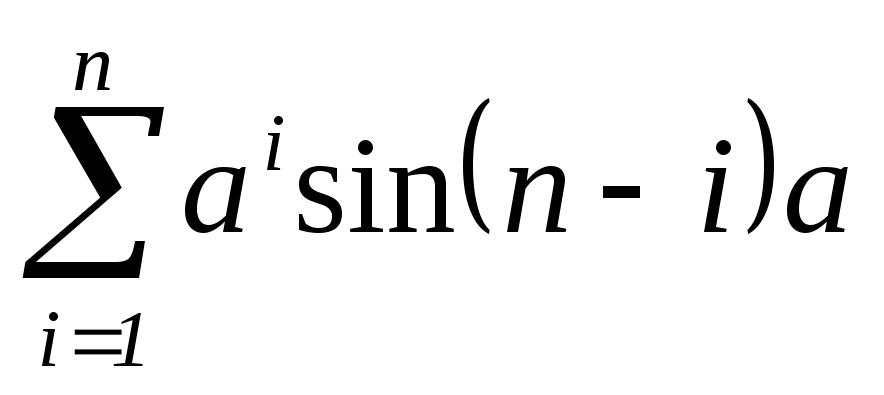 для
любого заданного a.
для
любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
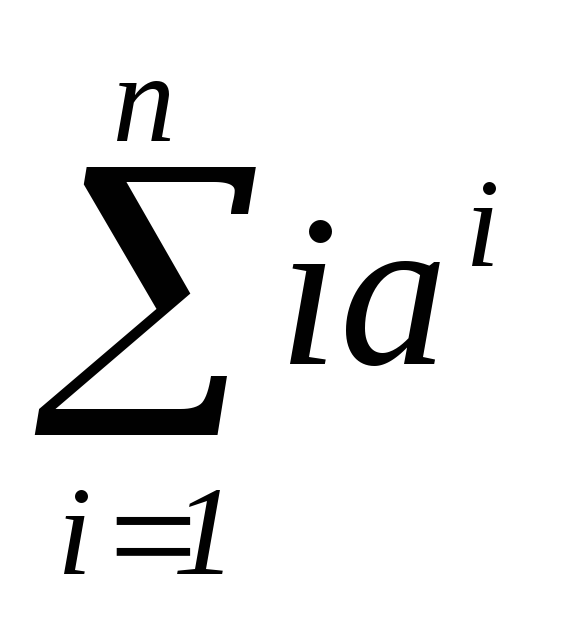 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для любого заданного a.
для любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы
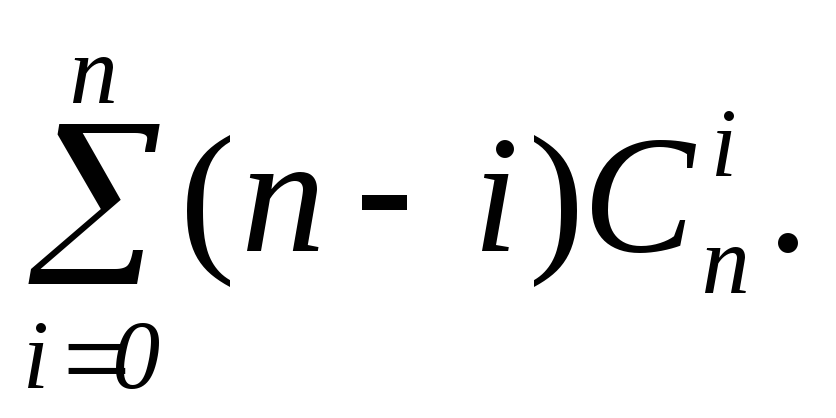
-
Напишите оптимальную по быстродействию программу для вычисления значения суммы
 для
любого заданного a.
для
любого заданного a. -
Напишите оптимальную по быстродействию программу для вычисления значения суммы

-
Дано натуральное n, вычислить n!
-
Даны два натуральных числа a и b, не равные нулю одновременно. Вычислить НОД (a,b) - наибольший общий делитель а и b.
-
Составить программу, печатающую квадраты всех натуральных чисел от 0 до заданного натурального n.
-
Составить программу, печатающую разложение на простые множители заданного натурального числа n > 0 (другими словами, требуется печатать только простые числа и произведение напечатанных чисел должно быть равно n; если n = 1, печатать ничего не надо).
-
Проверить, является ли заданное натуральное число n > 1 простым.
-
Дано натуральное n. Подсчитать количество решений неравенства x*x + y*y < n в натуральных (неотрицательных целых) числах, не используя действий с вещественными числами.
-
Даны натуральные числа а и b, причем b > 0. Найти частное и остаток при делении а на b, оперируя лишь с целыми числами и не используя операции целочисленного деления и нахождения остатка от деления, за исключением деления на 2 четных чисел; число шагов не должно превосходить C1*log(a/b) + C2 для некоторых констант C1, C2.
-
Подсчитать количество нулей в массиве x. (Составить фрагмент программы, не меняющий значения x, после исполнения которого значение некоторой целой переменной k равнялось бы числу нулей среди компонент массива x.)
-
Дан массив x длины n из целых чисел, причём x[1] <= x[2] <= ... <= x[n]. Найти количество различных чисел среди элементов этого массива.
-
Дан массив x [1]..x[n] целых чисел. Не используя других массивов, переставить элементы массива в обратном порядке.
-
Дан массив целых чисел x[1]..x[m+n], рассматриваемый как соединение двух его отрезков: начала x[1]..x[m] длины m и конца x[m+1]..x[m+n] длины n. Не используя дополнительных массивов, переставить начало и конец. (Число действий порядка m+n.)
-
Коэффициенты многочлена хранятся в массиве a: array [0..n] of integer (n - натуральное число, степень многочлена). Вычислить значение этого многочлена в точке x (т. е. a[n]*(x в степени n)+...+a[1]*x+a[0]).
-
В массивах a:array [0..k] of integer и b: array [0..l] of integer хранятся коэффициенты двух многочленов степеней k и l. Поместить в массив c: array [0..m] of integer коэффициенты их произведения. (Числа k, l, m - натуральные, m = k + l; элемент массива с индексом i содержит коэффициент при x в степени i.)
-
Даны два возрастающих массива x: array [1..k] of integer и y: array [1..l] of integer. Найти количество общих элементов в этих массивах (т. е. количество тех целых t, для которых t = x[i] = y[j] для некоторых i и j). (Число действий порядка k+l.)
-
Даны два неубывающих массива x: array [1..k] of integer и y: array [1..l] of integer. Найти число различных элементов среди x[1],...,x[k], y[1],...,y[l]. (Число действий порядка k+l.)
-
Даны два массива x[1] <= ... <= x[k] и y[1] <= ... <= y[l]. "Соединить" их в массив z[1] <= ... <= z[m] (m = k+l; каждый элемент должен входить в массив z столько раз, сколько раз он входит в общей сложности в массивы x и y). Число действий порядка m.
-
Некоторое число содержится в каждом из трех целочисленных неубывающих массивов x[1] <= ... <= x[p], y[1] <= ... <= y[q], z[1] <= ... <= z[r]. Найти одно из таких чисел. Число действий должно быть порядка p + q + r.
-
Дан неубывающий массив положительных целых чисел a[1] <= a[2] <=...<= a[n]. Найти наименьшее целое положительное число, не представимое в виде суммы нескольких элементов этого массива (каждый элемент массива может быть использован не более одного раза). Число действий порядка n.
-
Дан массив a[1..n] и число b. Переставить числа в массиве таким образом, чтобы слева от некоторой границы стояли числа, меньшие или равные b, а справа от границы - большие или равные b.
-
Дан массив a[1]..a[n] и число m<=n. Для каждой группы из m стоящих рядом членов (таких групп, очевидно, n-m+1) вычислить ее сумму. Общее число действий должно быть порядка n.
-
Дана квадратная таблица a[1..n][1..n] и число m<=n. Для каждого квадрата размера m на m в этой таблице вычислить сумму стоящих в нем чисел. Общее число действий должно быть порядка n*n.
-
Написать программу, которая печатала бы все перестановки чисел 1..n по одному разу.
-
Перечислить все представления положительного целого числа n в виде суммы последовательности невозрастающих целых положительных слагаемых.
-
Имеется последовательность символов x[1]..x[n]. Определить, имеются ли в ней идущие друг за другом символы "abcd". (Другими словами, требуется выяснить, есть ли в слове x[1]..x[n] подслово "abcd".)
-
Дано натуральное n, вычислить n! (0!=1, n! = n * (n-1)!).
-
Дано натуральное n, вычислить 1/0!+1/1!+...+1/n!.
-
Даны два натуральных числа a и b, не равные нулю одновременно. Вычислить НОД (a,b) - наибольший общий делитель а и b.
-
Даны натуральные а и b, не равные 0 одновременно. Найти d = НОД (a,b) и такие целые x и y, что d = a*x + b*y.
-
Составить программу, печатающую квадраты всех натуральных чисел от 0 до заданного натурального n.
-
Составить программу, печатающую разложение на простые множители заданного натурального числа n > 0 (другими словами, требуется печатать только простые числа и произведение напечатанных чисел должно быть равно n; если n = 1, печатать ничего не надо).
-
Дано натуральное n. Подсчитать количество решений неравенства x*x + y*y < n в натуральных (неотрицательных целых) числах, не используя действий с вещественными числами.
-
Подсчитать количество нулей в массиве x. (Составить фрагмент программы, не меняющий значения x, после исполнения которого значение некоторой целой переменной k равнялось бы числу нулей среди компонент массива x.)
-
Дан массив x: array [1..n] of integer, причём x[1] <= x[2] <= ... <= x[n]. Найти количество различных чисел среди элементов этого массива.
-
В массивах a:array [0..k] of integer и b: array [0..l] of integer хранятся коэффициенты двух многочленов степеней k и l. Поместить в массив c: array [0..m] of integer коэффициенты их произведения. (Числа k, l, m - натуральные, m = k + l; элемент массива с индексом i содержит коэффициент при x в степени i.)
-
Даны два возрастающих массива x: array [1..k] of integer и y: array [1..l] of integer. Найти количество общих элементов в этих массивах (т. е. количество тех целых t, для которых t = x[i] = y[j] для некоторых i и j).
-
Дан массив x: array [1..n] of array [1..m] of integer, упорядоченный по "строкам" и по "столбцам":
