4.3 Постулат Планка. Абсолютное значение энтропии

По уравнениям (4.34) и (4.37) невозможно вычислить абсолютное значение энтропии системы. Такую возможность дает новое недоказуемое положение, которое было сформулировано Планком (1912). Согласно этому положению, называемому постулатом Планка энтропия индивидуального кристаллического вещества при абсолютном нуле равна нулю:

(4.39)

Постулат Планка справедлив только для индивидуальных веществ, кристаллы которых идеально построены, такие тела называются идеальными твердыми телами. Реальные кристаллы не являются таковыми. Поэтому реальные кристаллы при 0 К обладают энтропией больше нуля.

В соответствии с постулатом Планка уравнение (4.39) для идеального твердого тела примет вид:

(4.40)

Можно показать, что при очень низких температурах не только энтропия и теплоемкость твердого тела стремятся к нулю (как это установлено экспериментально), но и многие другие свойства твердых тел (объем тела, давление насыщенного пара и др.) изменяются с температурой так, что их производные по температуре стремятся к нулю. Этим объясняется принцип недостижимости абсолютного нуля, согласно которому никакие процессы не могут снизить температуру тела до абсолютного нуля.

Постулат Планка используется при термодинамических расчетах химических процессов для вычисления абсолютных значений энтропий химических соединений. Энтропия твердого вещества вычисляется по уравнению (4.40). Для вычисления необходимо знать экспериментальные значения теплоемкостей, определенные для возможно низких температур до 10 К или 80 К. Значения теплоемкостей до 0 К находят путем экстраполяции по уравнениям Дебая или Тарасова либо с помощью эмпирических приемов.

Уравнение для вычисления энтропии газа при некоторой температуре будет иметь вид:

, (4.41)

где и_. – удельные теплоты агрегатных превращений.

Очевидно, что энтропию вещества, находящегося в жидком состоянии при температуре , также можно вычислить по уравнению (4.41), исключив два последних члена в правой части:

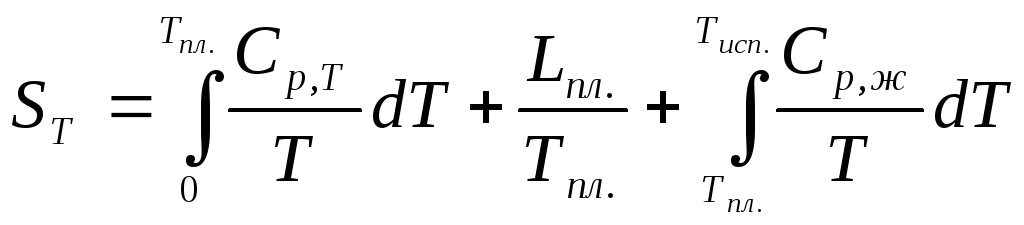(4.42)

Интегральные члены уравнения (4.42) находят графическим интегрированием. Для этого строят кривые и численное значение интеграла определяют по величине площади, ограниченной кривой и осью

абсцисс, заключенными между соответствующими температурами. Однако для расчета энтропии требуется выполнить серию точных и трудных экспериментальных исследований.

4.4 Характеристические функции. Приложение второго закона термодинамики

4.4.1 Изохорно-изотермический потенциал

Работа процесса в общем случае зависит от пути процесса. Работа неравновесного процесса меньше, чем работа равновесного процесса, протекающего между теми же начальными и конечными состояниями системы. Исходя из уравнения первого закона термодинамики (4.2) и уравнения (4.33), получаем в общем случае:

(4.43)

Величина правой части этого уравнения не зависит от того равновесен или не равновесен процесс. В случае равновесного процесса:

(4.44)

Для неравновесного процесса:

< (4.45)

Сравнивая уравнения (4.44) и (4.45), получаем:

.>

Таким образом, работа равновесного процесса максимальна.

Максимальная работа не зависит от пути, а определяется лишь начальным и конечным состоянием системы. Так, при (равновесный адиабатный процесс):

и ,

т.е. величина максимальной работы определяется изменением внутренней энергии системы.

Интегрируя при постоянной уравнение (4.44), получим:

(4.46)

или

(4.47)

Выражения, стоящие в скобках являются функциями состояния системы. Введя в уравнение (4.47) обозначение:

, (4.48)

получаем (при ):

, (4.49)

где – функция состояния, называемая изохорно-изотермическим потенциалом (более коротко – изохорным потенциалом) илисвободной энергией системы. Таким образом, максимальная работа при изохорно-изотермических равновесных процессах равна убыли свободной энергии системы.

Переписав уравнение (4.49) в виде , можно рассматривать внутреннюю энергию, как состоящую из двух частей - свободной энергиии связанной энергии.

Лишь часть внутренней энергии – свободная энергия, которую система отдает вовне при , может превратиться в работу (условием такого превращения является равновесность процесса; в неравновесном процессе свободная энергия частично и полностью переходит в теплоту). Другая часть внутренней энергии – связанная энергия – при изменении системы прине дает работы, а переходит только в теплоту:.

Таким образом, энтропия есть фактор емкости связанной энергии.

Полный дифференциал функции можно получить, дифференцируя уравнение (4.48):

(4.50)

Сопоставив это уравнение с уравнениями (4.44) и (4.45), получим в общем виде:

(4.51)

Откуда при или

(4.52)

Выражение (4.52) отражает уже известное положение, что работа неравновесного процесса меньше работы равновесного процесса.

Если при равновесном процессе совершается только работа расширения (), то из уравнения (4.51) получаем:

(4.53)

Это выражение является полным дифференциалом функции при переменныхи. Частные производные этой функции:

(4.54)

всегда отрицательны. Следовательно, изохорный потенциал убывает при возрастании объема и при возрастании температуры. Мерой убыли изохорного потенциала системы при возрастании температуры (при условии ) является энтропия системы.

Полагая и, а также при условии отсутствия всех других видов работы (), получаем из уравнения (4.51):

, (4.55)

т.е. изохорный потенциал системы, находящейся при постоянных и, не изменяется при равновесных процессах и убывает при неравновесных процессах.

Изохорный потенциал, являясь производным понятием по отношению к энтропии, представляет собой более удобный практически критерий направления процессов, чем энтропия.

Таким образом, изохорный потенциал системы, находящейся при постоянных объеме и температуре, стремится уменьшиться в естественных самопроизвольных процессах. Когда он достигает минимального значения, система приходит в равновесие.

Условия равновесия для системы при постоянных объеме и температуре:

; (4.56)