1. Тема 3. Средние величины

3.1 Основные понятия и формулы

Средней величиной называется обобщающий показатель, выражающий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.

Первым условием научного использования средней величины является качественно однородная совокупность, поэтому расчет средней сочетается с методом группировок. Второе условие – средняя должна исчисляться на основе данных в большом числе единиц, так как в этом случае колебания в величине признака, вызванные случайными причинами, погашаются, и проявляется общее свойство для всей совокупности.

Средняя, рассчитанная по совокупности в целом, называется общей средней.

Средние рассчитанные для каждой группы – групповыми средними.

Существует две категории средних величин:

1. Степенные средние (средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая и др.);

2. Структурные средние (мода и медиана).

Величины, для которых исчисляется средняя, обозначаются (варианты). Средняя обозначается через . Частота – повторяемость индивидуальных значений признака – обозначается символом . Частоты могут быть выражены не только абсолютными величинами, но и относительными – частостями .

Выбор формулы для расчета средней зависит от наличия исходной информации, задачи исследования, экономической сущности oсредняемого показателя (табл. 3.1).

Простая средняя арифметическая применяется в тех случаях, когда каждая из вариант х_i встречается в изучаемом явлении один или одинаковое количество раз.

Средняя арифметическая взвешенная вычисляется в тех случаях, когда различные варианты встречаются в изучаемой совокупности неодинаковое число раз ( число раз). Или когда не известен числитель и известен знаменатель выражения для расчета средней величины.

Средняя гармоническая применяется в тех случаях, когда известен числитель и не известен знаменатель выражения для расчета средней величины.

Средняя геометрическая рассчитывается, если индивидуальные значения признака х_i представляют собой относительные величины динамики, построенные в виде цепных коэффициентов. По этой формуле рассчитывается средний коэффициент роста.

Средняя квадратическая используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения.

Таблица 3.1 – Формулы для расчета различных видов степенных средних величин

Вид средней величины	Формула средней величины
	простая	Взвешенная
Арифметическая
Квадрати-ческая
Гармоническая		;
Геометрическая

Мода и медиана представляют собой средние величины, используемые в качестве вспомогательных обобщающих характеристик при изучении структуры совокупности.

Модой называется величина признака, которая чаще всего встречается в совокупности. В дискретном вариационном ряду для определения моды не требуется особых вычислений. В интервальном вариационном ряду для нахождения моды используется формула:

, (3.1)

где Мо – мода;

–нижняя граница модального интервала (интервала с наибольшей частотой или частостью );

–величина модального интервала;

–частота модального интервала;

–частота интервала, предшествующего модальному;

–частота интервала, следующего за модальным.

Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности вариант (значений признака) части.

В дискретном вариационном ряду определение медианы зависит от числа членов ряда n: если n – четное число, то медианой будет средняя арифметическая из двух срединных вариант, если n – нечетное число, то медианой будет средний член ряда по порядку, т.е. варианта с номером:

, (3.2)

где n – число членов ряда.

В интервальном вариационном ряду сначала определяют место (номер) медианного значения по формуле:

, (3.3)

где n – число членов ряда.

Медиану определяют по формуле:

, (3.4)

где Ме – медиана;

–нижняя граница медианного интервала;

–величина медианного интервала;

–сумма частот ряда;

–частота медианного интервала;

–накопленная частота интервала, предшествующего медианному (сумма частот интервалов, предшествующих медианному).
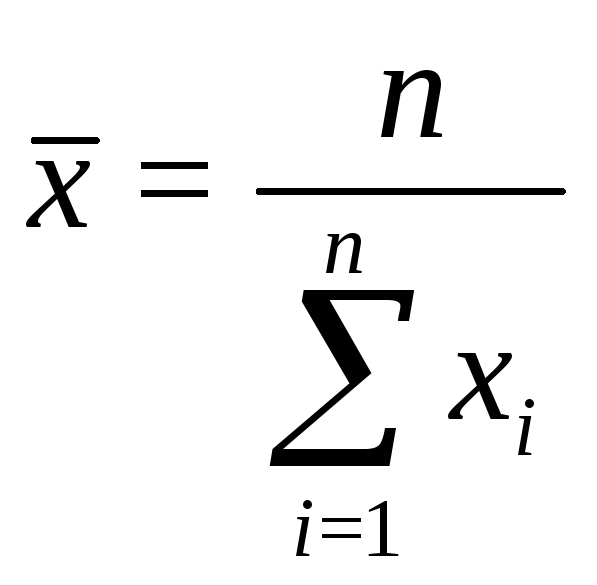