
Решение:
В ходе изложения
решения задачи будем рассматривать
запись алгоритма на языке Паскаль.
1)
Заметим, что в программе есть цикл, в
котором переменная t
принимает последовательно все целые
значения на отрезке ![]() :
:
 До
начала цикла в переменную M
записывается значение a,
а в переменную R –
значение функции в точке a:
До
начала цикла в переменную M
записывается значение a,
а в переменную R –
значение функции в точке a:
![]() .
Внутри
цикла есть условный оператор, в котором
вычисляется значение функции F(t)
и сравнивается со значением
переменной R:
.
Внутри
цикла есть условный оператор, в котором
вычисляется значение функции F(t)
и сравнивается со значением
переменной R:
 Если
новое значение функции меньше, чем
значение R,
в R
записывается значение функции в точке t,
а в переменной M
запоминается само значение t
(аргумент функции, соответствующий
значению R).
Таким
образом, понятно, что в данном алгоритме
осуществляется поиск минимума функции F(t)
на отрезке
Если
новое значение функции меньше, чем
значение R,
в R
записывается значение функции в точке t,
а в переменной M
запоминается само значение t
(аргумент функции, соответствующий
значению R).
Таким
образом, понятно, что в данном алгоритме
осуществляется поиск минимума функции F(t)
на отрезке ![]() ,
и после выполнения цикла в переменной M
оказывается значение аргумента t,
при котором функция достигает минимума
на заданном отрезке
,
и после выполнения цикла в переменной M
оказывается значение аргумента t,
при котором функция достигает минимума
на заданном отрезке ![]() Значение переменной М
выводится на печать.
2) Запишем заданную
в программе функцию в виде квадратного
трехчлена
Значение переменной М
выводится на печать.
2) Запишем заданную
в программе функцию в виде квадратного
трехчлена
![]() и
найдем точку минимума этой функции на
отрезке
и
найдем точку минимума этой функции на
отрезке ![]() Как
известно, для функции
Как
известно, для функции
![]() в
критической точке
в
критической точке
![]() при
a > 0
будет минимум.
Так как в нашем случае
a > 0,
то
при
a > 0
будет минимум.
Так как в нашем случае
a > 0,
то
![]() –
точка минимума, что и требовалось
определить.
Ответ:
2.
–
точка минимума, что и требовалось
определить.
Ответ:
2.
|
Задание B15. |
|
Сколько
существует различных наборов значений
логических переменных Х1, Х2, …, Х9, Х10,
которые удовлетворяют всем перечисленным
ниже условиям?
|
Решение:
Введем новые
обозначения:
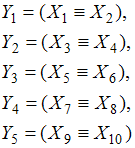 и,
учитывая, что
и,
учитывая, что
![]() тогда
и только тогда, когда
тогда
и только тогда, когда
![]() ,
перепишем
заданную систему в виде:
,
перепишем
заданную систему в виде:
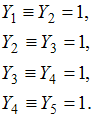 Заметим,
что все переменные здесь независимы
друг от друга.
Найдем решение этой
системы относительно независимых
переменных
Заметим,
что все переменные здесь независимы
друг от друга.
Найдем решение этой
системы относительно независимых
переменных
![]() .
В
соответствии с таблицей истинности
эквивалентности
.
В
соответствии с таблицей истинности
эквивалентности
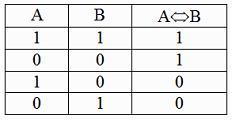 первое
уравнение
первое
уравнение ![]() имеет два решения: (0, 0) и (1, 1), а с
учетом остальных переменных – две
группы решений: (0, 0, *) и (1, 1, *),
где * обозначает остальные переменные,
которые могут быть любыми.
Второе
уравнение
имеет два решения: (0, 0) и (1, 1), а с
учетом остальных переменных – две
группы решений: (0, 0, *) и (1, 1, *),
где * обозначает остальные переменные,
которые могут быть любыми.
Второе
уравнение
![]() тоже
имеет две группы решений: (x1, 0, 0, *)
и (x1, 1, 1,*),
где x1
обозначает некоторое значение
переменной X1.
Теперь
ищем решения, которые удовлетворяют и
первому, и второму уравнению. Очевидно,
что их всего 2: (0, 0, 0, *) и
(1, 1, 1, *).
Рассуждая дальше
аналогичным образом, приходим к выводу,
что система имеет всего два решения
относительно переменных
тоже
имеет две группы решений: (x1, 0, 0, *)
и (x1, 1, 1,*),
где x1
обозначает некоторое значение
переменной X1.
Теперь
ищем решения, которые удовлетворяют и
первому, и второму уравнению. Очевидно,
что их всего 2: (0, 0, 0, *) и
(1, 1, 1, *).
Рассуждая дальше
аналогичным образом, приходим к выводу,
что система имеет всего два решения
относительно переменных ![]() :
все нули и все единицы.
Теперь нужно
получить количество решений в исходных
переменных
:
все нули и все единицы.
Теперь нужно
получить количество решений в исходных
переменных
![]() Для
этого вспомним, что переменные
Для
этого вспомним, что переменные
![]() независимы.
Предположим,
что значение Y1
известно: (0 или 1). Поскольку
независимы.
Предположим,
что значение Y1
известно: (0 или 1). Поскольку ![]() ,
по таблице истинности эквивалентности
,
по таблице истинности эквивалентности
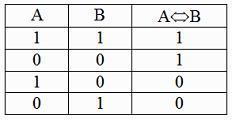 получаем
две
соответствующих пары (X1; X2):
как для случая Y1 = 0,
так и для
случая
Y1 = 1.
У
нас есть 5 переменных
получаем
две
соответствующих пары (X1; X2):
как для случая Y1 = 0,
так и для
случая
Y1 = 1.
У
нас есть 5 переменных
![]() ,
каждая их комбинация дает 2 допустимые
пары (X1; X2),
2 пары (X3; X4),
2 пары (X5; X6),
2 пары (X7; X8)
и 2 пары (X9; X10),
то есть всего 25 = 32
комбинации исходных переменных.
Таким
образом, общее количество
решений 2 * 32 = 64.
Ответ:
64.
,
каждая их комбинация дает 2 допустимые
пары (X1; X2),
2 пары (X3; X4),
2 пары (X5; X6),
2 пары (X7; X8)
и 2 пары (X9; X10),
то есть всего 25 = 32
комбинации исходных переменных.
Таким
образом, общее количество
решений 2 * 32 = 64.
Ответ:
64.
|
Задание C1. |
|
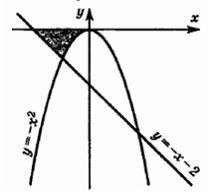
Требовалось
написать программу, при выполнении
которой с клавиатуры считываются
координаты точки на плоскости (x, y –
действительные числа) и определяется
принадлежность этой точки заданной
закрашенной области (включая
границы).
|

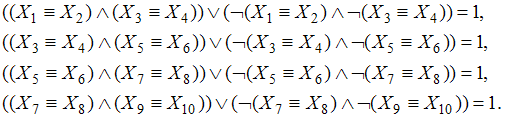 В
ответе не нужно перечислять все
различные наборы значений Х1, Х2, …, Х9, Х10,
при которых выполнена данная система
равенств. В качестве ответа вам нужно
указать количество таких наборов.
В
ответе не нужно перечислять все
различные наборы значений Х1, Х2, …, Х9, Х10,
при которых выполнена данная система
равенств. В качестве ответа вам нужно
указать количество таких наборов.
 Программист
торопился и написал программу
неправильно.
Программист
торопился и написал программу
неправильно.
 Последовательно
выполните следующее.
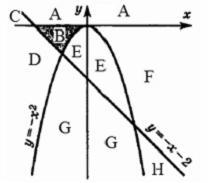
1. Перерисуйте
и заполните таблицу, которая показывает,
как работает программа при аргументах,
принадлежащих различным областям
(A, B, C, D, E, F, G и H).
Последовательно
выполните следующее.
1. Перерисуйте
и заполните таблицу, которая показывает,
как работает программа при аргументах,
принадлежащих различным областям
(A, B, C, D, E, F, G и H).
 Точки,
лежащие на границах областей, отдельно
не рассматривать.
Точки,
лежащие на границах областей, отдельно
не рассматривать.
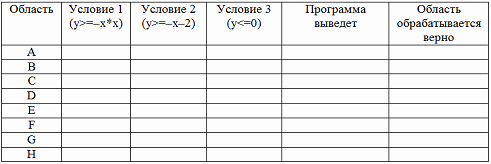 В
столбцах условий укажите «да», если
условие выполнится, «нет», если условие
не выполнится, «–» (прочерк), если
условие не будет проверяться, «не изв.»,
если программа ведет себя по-разному
для разных значений, принадлежащих
данной области. В столбце «Программа
выведет» укажите, что программа выведет
на экран. Если программа ничего не
выводит, поставьте «–» (прочерк).
Если для разных значений, принадлежащих
области, будут выведены разные тексты,
напишите «не изв.». В последнем
столбце укажите «да» или «нет».
2.
Укажите, как нужно доработать программу,
чтобы не было случаев ее неправильной
работы. (Это можно сделать несколькими
способами, достаточно указать любой
способ доработки исходной
программы.)
Выполните
задание и сравните с предлагаемым
решением.
В
столбцах условий укажите «да», если
условие выполнится, «нет», если условие
не выполнится, «–» (прочерк), если
условие не будет проверяться, «не изв.»,
если программа ведет себя по-разному
для разных значений, принадлежащих
данной области. В столбце «Программа
выведет» укажите, что программа выведет
на экран. Если программа ничего не
выводит, поставьте «–» (прочерк).
Если для разных значений, принадлежащих
области, будут выведены разные тексты,
напишите «не изв.». В последнем
столбце укажите «да» или «нет».
2.
Укажите, как нужно доработать программу,
чтобы не было случаев ее неправильной
работы. (Это можно сделать несколькими
способами, достаточно указать любой
способ доработки исходной
программы.)
Выполните
задание и сравните с предлагаемым
решением.